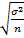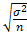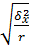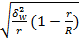Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Индексный анализ территориальных различийСодержание книги
Поиск на нашем сайте
Первый вариант расчета территориальных индексов заключается в том, что в качестве весов принимаются объемы проданных товаров i-го вида (I = 1, 2,..., п) по двум регионам, вместе взятым
Территориальный индекс цен в этом случае рассчитывается по следующей формуле:
При расчете индексов могут выступать показатели каждой территории, при этом, они могут быть, как в числителе, так и в знаменателе.
Полученные в результате индексы будут различаться по величине так же, как различаются по величине индексы Ласпереса и Пуаше.
Территориальный индекс имеет отличие в соизмерителе.
Числитель по региону б, знаменатель по региону а. 72+44=116 15+12=27 60+55=115 I=(9*116+4*27+10*115)/(7*116+5*27+8*115)=1,233
Второй возможный способ расчета территориальных индексов учитывает соотношение весов на каждой из сравниваемых территорий. При этом способе, прежде всего, необходимо рассчитать средние цены каждого товара по двум территориям, вместе взятым
Расчет территориального индекса базируется на сравнении уровней цен каждого региона со средними ценами
I=((9*44+4*12+10*55)/(7,8*44+4,6*12+9*55))/ ((7*72+5*15+8*60)/(7,8*72+4,6*15+9*6))=1,23
EKSB/A=
Метод Гири-Камиса:
Индекс развития человеческого потенциала относится к агрегатным индексам, включает в себя множество других индексов (индекс образования, ожидаемой продолжительности жизни, реального ВВП на душу населения).
Выборочное наблюдение
1. Понятие о выборочном наблюдении и области его применения. 2. Ошибки выборочного наблюдения. 3. Способы формирования выборочной совокупности. 4. Определение необходимого объема выборки. 5. Оценка результатов выборочного наблюдения и распространение их на генеральную совокупность. 6. Малая выборка.
Символы основных характеристик параметров генеральной и выборочной совокупностей
Греческие Латинские
Под выборочным наблюдением понимается несплошное наблюдение, при котором статистическому наблюдению подвергаются единицы совокупности, отобранные случайным способом.
Задачи: статистически оценить и проверить гипотезы; решить некоторые производственные и управленческие задачи; оценить отраслевые показатели, развитие отраслей; решить задачи в сфере предпринимательской деятельности.
Оценить и проверить гипотезы, значит должны на основе выбора лучшей оценки (моды, медианы), отобрать наилучшие выборочные параметры оценок.
Решить производственные и управленческие задачи, значит отобрать и создать систему показателей качества, которые могли бы контролировать производственный процесс, должны оценить отклонение от технологического и производственного режимов, должны на базе этого предложить альтернативные технологии на базе произведенных замеров.
Задачи отраслевых показателей сводятся к определению рабочего времени, продуктивности и т.д.
Ошибка выборочного наблюдения - это разность между величиной параметра в генеральной совокупности и его величиной, вычисленной по результатам выборочного наблюдения.
x̅=
Величина называется предельной ошибкой выборки.
В теореме П. Л. Чебышева доказано, что величина ошибки не должна превышать tμ. В свою очередь, величина μ, выражающая среднее квадратическое отклонение выборочной средней от генеральной средней, зависит от колеблемости признака в генеральной совокупности σ и числа отобранных единиц n. Эта зависимость выражается формулой
Величину — называют средней ошибкой выборки и обозначают μ.
n – объем выборочной совокупности
При обобщения результатов выборочного наблюдения наиболее часто используются следующие уровни вероятности и соответствующие им значении t
t=1F(t)=0,683 t=2F(t)=0,954 t=3F(t)=0,997 t=1.5F(t)=0,866 t=2.5F(t)=0,988 t=3.5F(t)=0,999
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 209; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.105.199 (0.006 с.) |


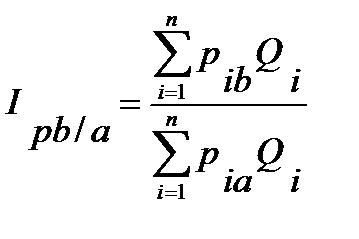

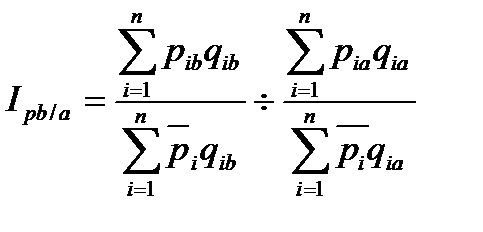
 = (7*72+9*44)/116=7,8
= (7*72+9*44)/116=7,8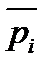 =(5*15+4*12)/27=4,6
=(5*15+4*12)/27=4,6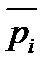 =(8*60+10*55)=9
=(8*60+10*55)=9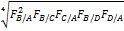
 (i=1,2,…,N)
(i=1,2,…,N)
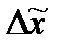 = | x̅ -
= | x̅ - 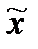 |
|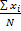
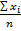
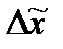
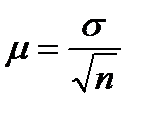

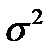 - генеральная совокупность
- генеральная совокупность