Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статистическая сводка и группировкаСодержание книги
Поиск на нашем сайте
Статистика как наука
Статистика – одна из общественных наук, имеющая целью сбор, упорядочивание, анализ и сопоставление числового представления фактов, относящихся к самым разнообразным массовым явлениям. Учение о системе показателей.
Структура статистики: 1. Общая теория статистики; 2. Экономическая статистика; 3. Социальная статистика; 4. Другие (отраслевые) виды статистики.
Статистика – общественная наука, которая изучает количественную сторону качественного определенных массовых социально-экономических явлений и процессов, их структуру и распределение, размещение в пространстве, движение во времени, выявляя действующие количественные зависимости, тенденции и закономерности, причем в конкретных условиях места и времени.
Предметом статистики выступают размеры и количественные отношения социально-экономических явлений, закономерности их развития.
Объект – самые разнообразные социально-экономические явления, процессы общественной жизни.
Задачи: 1. Изучение уровня и структуры массовых социально-экономических явлений; 2. Изучение взаимосвязей массовых социально-экономических явлений; 3. Обобщение и прогнозирование тенденций развития хозяйственного механизма; 4. Динамика массовых социально-экономических явлений; 5. Выявление резервов эффективности общественного производства; 6. Внедрение в статистику стандартов системы национальных счетов.
Статистическая совокупность – множество единиц, обладающих массовостью, однородностью, определенной целостностью, взаимозависимостью состояний отдельных единиц и наличием вариаций.
Вариация – количественные изменения значений признака при переходе от одной единицы совокупности к другой.
Признаки: 1. Атрибутивные (описательные, качественные); 2. Количественные – выражаются итоговыми значениями.
Признаки: 1. По содержательности: · Существенные; · Несущественные; · Первичные; · Вторичные; 2. По принадлежности: · Индивидуальные; · Общие; 3. По направлению: · Прямые; · Косвенные; 4. По степени детерминированности: · Детерминированные; · Статистические; · Стохастические.
Статистические закономерности – повторяемость, последовательность и порядок изменений в явлениях.
Статистические показатели – отражает результат измерения.
Атрибуты: · Количественная определенность; · Место и время/период.
Система показателей – совокупность показателей, всесторонне отражающих сложное явление.
Объемный показатель – измерение объема статистической совокупности или ее частей.
Статистическая методология – система приемов, способов, методов, направленных на изучение количественных закономерностей, происходящих в структуре, динамике и взаимодействии социально-экономических явлений.
Статистическое наблюдение
Статистическая информация – совокупность явлений социально-экономического характера, полученных в результате статистического наблюдения, на основе которых осуществляется учет и контроль, планирование, статистический анализ и управление.
Статистическое наблюдение – научно-организованный, планомерный и систематический процесс сбора массовых сведений о социально-экономических явлениях и процессах путем регистрации заранее намеченных существенных признаков.
Процесс проведения статистического наблюдения: 1. Программно-методологическая подготовка: · Определение цели; · Составление признаков, подлежащих регистрации; · Разработка документов для сбора данных; · Выбор отчетной единицы; · Определение методов получения данных; 2. Организационная подготовка: · Подбор и подготовка кадров; · Составление календарного плана работ; · Подготовка технической документации; 3. Выбор формы, способа и вида статистического наблюдения; 4. Проведение наблюдения; 5. Синтаксический, логический и арифметический контроль данных; 6. Выборка выводов и предложений по проведению наблюдения.
Программа наблюдения: 1. Формирование целей и задач. Цель должна быть сформулирована четко, с указанием конкретных задач, стоящих перед проводимым наблюдением; 2. Определение объекта и единиц наблюдения. Объект – совокупность единиц изучаемого явления, который подвергается статистическому явлению. Единица – первичный составной элемент объекта наблюдения, являющийся носителем регистрационных признаков; 3. Разработка программы наблюдения; 4. Оформление программы. Статистический формуляр – документ единого образца, содержащий программу и результаты наблюдения. · Индивидуальный; · Списочный.
Организационный план: · Объект; · Цели и задачи; · Органы наблюдения; · Место и время; · Сроки наблюдения; · Кадры, отвечающие за проведение наблюдения.
Классификация наблюдений: 1. Организационные формы: · Отчетность: ü Общегосударственная; ü Внутриведомственная; · Статистическое обследование: ü Переписи населения; ü Бюджетные обследования домашних хозяйств; ü Структура потребительских расходов и доходов; · Регистры: ü Регистр населения; ü Регистр предприятий; 2. Виды проведения: · По охвату единиц населения: ü Сплошное (перепись населения); ü Несплошное: выборочное, метод основного массива, монографическое; · По срокам регистрации: ü Непрерывное; ü Прерывное: периодическое, единовременное; · По источникам сведений: ü Непосредственное; ü Документальное; ü Опрос; 3. Способы проведения: · Отчетный; · Экспедиционный; · Самоисчисление; · Анкетный; · Корреспондентский.
Ошибки статистического наблюдения: 1. Абсолютная ошибка – разность фактических данных изучаемых признаков и данных, полученных в ходе статистического наблюдения. 2. Относительная ошибка.
Ошибками статистического наблюдения называются расхождения между установленными статистическим наблюдением и действительными значениями изучаемых величин.
Выделяют ошибки регистрации и ошибки репрезентативности.
Ошибки регистрации – отклонение между значением показателя полученного в ходе статистического наблюдения, и фактическим, действительным значением.
Отклонение значения показателя обследованной совокупности от его величины по исходной совокупности называется ошибкой репрезентативности.
Виды контроля: 1. Синтаксический - проверка правильности структуры документа, наличия необходимых реквизитов, оформления документов на предмет наличия и четкости всех необходимых записей. 2. Логический – сопоставление ответов на взаимосвязанные вопросы статистического формуляра или другого документа статистического или социологического обследования с целью выявления логической совместимости ответов и основывается на знании логических взаимосвязей между показателями. 3. Счетный (арифметический) – показывает какая зависимость не выполняется.
Графическое представление рядов распределения Анализ рядов распределения можно наглядно проводить на основе их графического изображения. Для этой цели строят полигон, гистограмму, огиву и кумуляту распределения.
Полигон используется при изображении дискретных вариационных рядов.
Гистограмма применяется для изображения интервального вариационного ряда. Гистограмма может быть преобразована в полигон, если середины верхних сторон прямоугольников соединить.
Для графического изображения вариационных рядов может использоваться кумулятивная кривая. При помощи кумуляты изображается ряд накопленных частот.
Если при графическом изображении вариационного ряда в виде кумуляты оси поменять места, то получим огиву. Статистические показатели
Средние величины
Средняя величина признака – обобщающий показатель, характеризующий типический уровень явления.
Сущность средней заключается в том, что в ней взаимопогашаются отклонения значений признака отдельных единиц совокупности, обусловленные действием случайных факторов, и учитываются изменения, вызванные действием факторов основных.
Типичность средней непосредственным образом связана с однородностью статистической совокупности.
Средняя величина только тогда будет отражать типичный уровень признака, когда она рассчитана по качественно однородной совокупности (средняя зарплата по стране - статистическая).
Правила применения средних величин: — необходимо исходить из качественного содержания признака; — средняя величина должна рассчитываться по однородной совокупности; — необходим обоснованный выбор единицы совокупности.
При использовании средних величин введем такие обозначения: x̅ - среднее значение исследуемого признака хi или x - каждое индивидуальное значение (варианта в вариационном ряду) fi или f - частота повторений (вес) индивидуального признака w - объем значений признака n - количество единиц исследуемого признака
Средние величины подразделяются на степенные и структурные. Формулы расчета степенных средних можно записать в общем виде:
- простая формула - - взвешенная формула
при k=1 “средняя арифметическая”
при k=2 “средняя квадратическая”
при k=3 “средняя кубическая”
при k=-1 “средняя гармоническая”
“средняя геометрическая” (k=0)
С увеличение степени k значение степенной средней увеличивается, т.е. для одной и той же совокупности справедливо
x̅-1 ≤ x̅0 ≤ x̅1 ≤ x̅2 ≤ x̅3 ≤ …
т.е. при увеличении степени средняя величина увеличивается (правило мажоритарности средних). Пользуясь правилом статистика может в зависимости от настроения и желания ее «знатока» может как «утопить», так и «выручить».
Средняя арифметическая взвешенная При расчете величин отдельные значения осредняемого признака могут повторяться, встречаться по нескольку раз. В подобных случаях расчет средней производится сгруппированным данным или вариационным рядам, которые могут быть дискретными или интервальными.
Использовать среднюю арифметическую невзвешенную только тогда, когда точно установлено отсутствие весов или их равенство.
При расчете средней по интервальному вариационному ряду для выполнения необходимых вычислений от интервалов переходят к их серединам.
Способ моментов Если интервальный ряд имеет равные интервалы или дискретный ряд построен с одни и тем же шагом между ближайшими значениями признака, для расчета средней применим способ моментов.
Алгоритм: 1. строится новый дискретный ряд распределения, в котором один из вариантов приравнивается к нулю. 2. остальные варианты нового ряда обозначаются и рассчитываются по формуле: x`=(x-x0)/h h – ширина равного интервала или шага x` - условные варианты 3. определяется средняя по способу моментов.
Свойства средней арифметической Средняя арифметическая обладает некоторыми математическими свойствами, более полно раскрывающими ее сущность и в ряде случаев используемыми при ее расчетах. Рассмотрим эти свойства 1. произведение средней на сумму частот равно сумме произведений отдельных вариантов на соответствующие им частоты 2. сумма отклонений индивидуальных значений признака от средней арифметической равна нулю 3. если все осредняемые варианты увеличить или уменьшить на постоянное число А, то средняя арифметическая увеличится или уменьшится на ту же величину. 4. Если все варианты значений признака уменьшить или увеличить в А раз, то средняя также соответственно уменьшится или увеличится в А раз. 5. Если все веса уменьшить или увеличить в А раз, то средняя арифметическая от этого не изменится. Исходя из данного свойства можно заключить, что в случае равенства всех весов между собой расчеты по средней арифметической взвешенной и средней арифметической простой приведут к одному и тому е результату.
Другие виды средних При расчете статистических показателей помимо средней арифметической могут использоваться и другие виды средних.
Средняя квадратическая - Применяется для осреднения величин, выраженных в виде квадратных функций (например, средние диаметры колес, труб, стволов, средние стороны квадратов и др.). Используется при расчете показателей вариации (СКО).
Средняя кубическая - применяется, когда необходимо сохранить неизменной сумму кубов исходных величин. Находятся: строительные объемы зданий, элеваторов, бассейнов.
Средняя гармоническая взвешенная. Рассмотрим вариант, когда известен числитель исходного соотношения средней, но неизвестен его знаменатель. Средняя гармоническая может применяться для усреднения тех же признаков, но с другой формой представления данных. Может быть не только взвешенной, но и простой.
Средняя геометрическая обладает свойством сохранять неизменным произведение исходных величин. Применяется для усреднения относительных величин, а также для нахождения качественного среднего между минимальным и максимальным значением.
Средняя хронологическая – применяется на временных рядах, может быть простой и взвешенной. Структурные характеристики вариационного ряда Мода (Мо) представляет собой значение изучаемого признака, повторяющееся с наибольшей частотой.
Медианой (Me) называется значение признака, приходящееся на середину ранжированной (упорядоченной) совокупности. Главное свойство: сумма абсолютных значений признака от медианы меньше, чем от любой другой величины
Определение моды в интервальных рядах:
xmo – начало модального интервала, h – ширина модального интервала, fmo – частота модального интервала, fmo-1,fmo+1 – частоты соседних интервалов.
Определение медианы в интервальных рядах:
xme – начало медианного интервала, Sme-1 – накопленная частота интервала, предшествующего медианному fme – частота медианного интервала
Соотношение моды, медианы и средней арифметической указывает на характер распределения признака в совокупности, позволяет оценить его асимметрию. Если Мо < Ме < x̅— имеет место правосторонняя асимметрия, при x̅ < Ме< Мо следует сделать вывод о левосторонней асимметрии ряда.
Аналогично с нахождением медианы в вариационных рядах распределения можно отыскать значение признака у любой по порядку единицы ранжированного ряда. Так, например, можно найти значение признака у единиц, делящих ряд на четыре равные части, на десять или сто частей. Эти величины называются «квартили», «децили»(10 частей) и «перцентили»(100 частей).
Квартили представляют собой значения признака, делящие ранжированную совокупность на четыре равновеликие части. Различают квартиль нижний (Q1), отделяющий 1/4 часть совокупности с наименьшими значениями признака, и квартиль верхний (Q 3), отсекающий 1/4 часть с наибольшими значениями признака. Это означает, что 25% единиц совокупности будут меньше по величине Q1; 25% единиц будут заключены между Q2 и Q3; 25% - между Q2 и Q3 и остальные 25% превосходят Q3. Средним квартилем Q2 является медиана.
Для расчета квартилей по интервальному вариационному ряду используются формулы:
Кроме квартилей в вариационных рядах распределения могут определяться децили - варианты, делящие ранжированный ряд на десять равных частей.
Показатели вариации
Вариацией признака называют отличие (колеблемость, многообразие, изменяемость величины) в численных значениях признаков единиц совокупности и их колебания около средней величины, что и будет характеризовать совокупность. Показатели вариации делятся на две группы: абсолютные и относительные. К абсолютным относятся размах вариации, среднее линейное отклонение, дисперсия и среднее квадратическое отклонение. Относительными показателями вариации являются коэффициенты осцилляции, вариации, относительное линейное отклонение и др. Самым простым абсолютным показателем является размах вариации (R).
Для анализа вариации необходим и показатель, который отражает все колебания варьирующего признака, дающий обобщенную ее характеристику. Такая средняя называется средним линейным отклонением (L). Оно вычисляется как средняя арифметическая из абсолютных значений отклонений вариант хi и (взвешенная или простая в зависимости от исходных условий) по следующим формулам:
- простое
- взвешенное
Дисперсия представляет собой средний квадрат отклонений индивидуальных значений признака от их средней величины и вычисляется по формулам простой и взвешенной дисперсий (в зависимости от исходных данных):
- простая
- взвешенная
— средняя квадратов вариант;
— квадрат средней вариант.
Т.о., дисперсия есть средняя величина квадратов отклонений.
– момент второго порядка;
– момент первого порядка;
– условные варианты
Дисперсию используют не только для оценки вариации, но и для измерения связей между исследуемыми факторами; распределение дисперсии на составляющие позволяет оценить влияние разных факторов, которые обусловливают вариацию признака. Среднее квадратическое отклонение, как и дисперсия, выступает в качестве широко используемого обобщающего показателя вариации.
В условиях нормального распределения существует следующая зависимость между величиной среднего квадратического отклонения и количеством наблюдений: в пределах х±1Ϭ располагается 0,683 или 98,3% количества наблюдений; в пределах х±2Ϭ – 95,4%; в пределах х±3Ϭ – 97,7%.
Линейный коэффициент вариации (характеризует долю усредненного значения абсолютных отклонений от средней арифметической). (VL):
Коэффициент вариации (характеризует степень однородности совокупности)(Vσ):
Индексы Общее понятие об индексах. Классификация индексов. Индивидуальные индексы. Система индексов. Средневзвешенные индексы. Классификация индексов Индексы могут быть классифицированы по таким признакам: а)мера охвата элементов совокупности: индивидуальные – относительные показатели, которые характеризуют изменения в динамике или отображают соотношение в пространства какого-либо одного вида единиц явления; общие – позволяют соединить разнородные явления, те явления, которые нельзя сложить ни во времени, ни в пространстве. б)база сравнения: базисные, цепные. в)вид объекта сравнения: динамические, территориальные, индексы сопоставления с планом. г)вид соизмерителя: постоянные, переменные соизмерители. д)форма построения: агрегатные, средние. ж) в зависимости от содержания и характера индексируемой величины: количественные, качественные. з) объект исследования: индексы физического объема продукции, производительности труда, стоимости продукции, индексы размера и структуры посевных площадей. к) состав явления: постоянного состава (изменяется одна величина), переменного состава (две и более величины), структурных сдвигов (отношение переменного состава к индексу постоянного состава). л) период расчета.
Индивидуальные индексы
Простейшим показателем, используемым в индексном анализе, является индивидуальный индекс, который характеризует изменение во времени экономических величин, относящихся к одному объекту (или однотоварных явлений). Примерами индивидуальных индексов являются такие:
Взаимосвязь между цепными и базисными индивидуальными индексами: произведение цепных индексов равняется базисному индексу крайних периодов; частное от деления последующего базисного индекса на предыдущий равняется соответствующему цепному индексу.
Агрегатная форма общего индекса. Сущность и принципы построения Агрегатные индексы являются основной формой общего индекса (от лат. aggrega — присоединяю). Свое название они получили потому, что характеризуют не отдельные единицы, а их группы (агрегаты). Одной из первых попыток агрегировать в индексе различные единицы совокупности можно считать формулу индекса цен французского экономиста Дюто, предложенную в 1738 г.:
где ∑p1 – сумма цен на отдельные товары в отчетном периоде; ∑p0 – сумма цен на те же товары в базисном периоде.
Д/З: Средняя часовая выработка рабочего в 3 квартале по сравнению со 2 выросла на 5%. Средняя фактическая продолжительность рабочего дня снизилась на 0,6%. Среднее число дней работы одного рабочего увеличилось на 1,7%. Доля численности рабочих в общей численности работающих возросла на 3%. Найти индивидуальные индексы. Найти индекс квартальной выработки работающего (выработка 1,05; 0,994; 1,107 = 1,0614)
В 1764г. Карли определил общий индекс цен как среднюю арифметическую простую из индивидуальных цен. Базисная цена в качестве соизмерителя была предложена в агрегатной форме индекса Ласпейресом в 1864г. В отечественной практике для расчета индекса количественного показателя чаще используют формулу Ласпейреса, качественного – Пааше.
Индекс физического объема продукции – наиболее типичный общий индекс количественных показателей. Изменение цен на продукции в текущем периоде по сравнению с базисным не влияет на величину индекса. Если объектом исследования является отдельное предприятие, то индекс определяется по совокупности произведенных товаров. Когда объект исследования – отрасль, то складываем совокупности всех произведенных товаров в отрасли. Если объектом исследования является регион, то индекс рассчитывается по всем предприятием региона. Индекс физического объема показывает во сколько раз возросла/уменьшилась стоимость продукции из-за роста/снижения объема его производства. Разность между числителем и знаменателем индекса показывает на сколько рублей изменилась стоимость продукции в результате роста/уменьшения ее объема.
Обозначения: • q1 – количество одноименных единиц продукции (объем продаж одноименного товара) в отчетном периоде; • q0 — количество одноименных единиц продукции (объем продаж одноименного товаpа) в базисном периоде; • р0 — цена одноименной единицы продукции (товара) в базисном периоде; • z0 — себестоимость одноименной единицы продукции в базисном периоде; • q1 p0 – стоимость выпуска одноименной продукции отчетного периода в ценах базисного периода(товарооборот одноименного товара отчетного периода в ценахбазисного периода); • q0 p0 – стоимость выпуска одноименной продукции в базисном периоде (товарооборот одноименного товарав базисном периоде); • ∑q1 p0 – стоимость выпуска разноименной продукции отчетного периода в ценах базисного периода (товарооборот разноименного товара отчетного периода в ценах базисного периода); • ∑q0 p0 – стоимость выпуска разноименной продукции в базисном периоде (товарооборот разноименных товаров в базисном периоде);
Индексы цен нужны для технико-экономических обоснований в проектном строительстве, при пересчете основных показателей Системы Национальных Счетов.
В настоящее время остается проблема подбора универсального соизмерителя в агрегатных индексах цен. Индексы цен рассчитываются не по всей совокупности продукции, а по тем продуктам, которые составляю товарную корзину. Поэтому товарная корзина в разных странах различна. В меньшей степени показывают в общем произведенную продукцию.
Индекс потребительских цен – универсальный измеритель. Он служит для пересмотра социальных программ, расчета минимальной заработной платы. Отражает реальную покупательную способность денег.
Методология расчета данного индекса: 1. Отбор товаров, услуг, представителей и торговых предприятий, по которым производится регистрация цен. 2. Формирование структуры весов по отдельным группам товаров и услуг для расчета сводного индекса потребительских цен. Для формирования структуры весов используются данные о структуре потребительских расходов населения. 3. Методология расчета потребительских цен предполагает, что индекс рассчитывается отдельно для регионов, товарных групп и отдельных групп населения.
Для индексов стоимостных показателей соизмерителей не требуется, достаточно произвести суммирование произведений качественного и количественного показателей.
Для взвешивания качественного показателя используется средний объем, то общий индекс называется индексом Лоу. Применяется когда нужно сделать расчеты за очень длительный период. Система индексов
Индексы позволяют получать сводную оценку изучаемых процессов постоянно, месяц за месяцем, год за годом. Однако при этом для достижения сопоставимости они должны рассчитываться по единой методологии. Такая методология или схема расчета индексом за несколько последовательных временных периодов называется системой индексов.
В зависимости от информационной базы и целей исследования индексная система может строиться по-разному. При этом используются цепные и базисные способы расчета.
Для индексов с постоянными соизмерителями: произведение цепных индексов равняется базисному индексу крайних периодов; частное от деления последующего базисного индекса с постоянными соизмерителями на предыдущий равняется цепному индексу.
Данные индексы с постоянными весами предпочтительнее потому что они мультипликативны по своей сущности, т.е. их можно последовательно перемножать.
Цепные индексы цен с переменными весами, с постоянными весами.
Система базисных индексов с переменными весами, с постоянными весами.
С помощью индексов можно определить абсолютный прирост итогового показателя мультипликативной модели, как в целом, так и по факторам этой модели. Для модели товарооборота:
Средневзвешенные индексы
Существуют две формы средневзвешенных индексов: • Среднеарифметическая. • Среднегармоническая. Как правило, средний арифметический индекс применяется при индексации количественных показателей (например, физического объема продукции), а средний гармонический — при индексации качественных показателей (например, цен).
Весами в формуле является стоимость продукции базисного периода. Так как iq х q0 = q1, то формула этого индекса легко преобразуется в формулу:
Средний арифметический индекс производительности труда определяется следующим образом:
Так как itх t1, = t0, то формула этого индекса может быть преобразована в агрегатный индекс трудоемкости продукции. Весами являются общие затраты времени на производство продукции в текущем периоде.
В статистике широко известен и другой средний арифметический индекс, который используется при анализе производительности труда. Он носит название индекса Струмилина.
Индексы других качественных показателей (цен, себестоимости и т. д.) определяются по формуле средней гармонической взвешенной величины.
Средний гармонический индекс тождествен агрегатному, если индивидуальные индексы будут взвешены с помощью слагаемых числителя агрегатного индекса. Тогда при расчете сводного индекса цен по методу Паше можно использовать следующую замену:
Сводный индекс цен будет выражен в форме сред ей гармонической,
а инд екс себестоимости можно исчислить так:
Общие (сводные) индексы средних величин
В экономико-статистическом анализе приходится сравнивать в динамике такие обобщающие характеристики качественных показателей как • средняя цена, • средняя себестоимость, • средняя производительность труда • средняя заработная плата и др.
Показывают изменение среднего значения индексируемого показателя. Применяются только для качественных показателей. Индексы средних величин применяются при обобщении данных не по элементам, а по единицам совокупности. Например: цена товара одного вида (элемента), продаваемого в разных торговых точках обобщается в виде средней (по предприятиям торговли) цены этого товара; себестоимость одного вида продукции обобщается в виде средней себестоимости данной продукции по совокупности производящих ее предприятий (т. е. по единицам совокупности). Средняя цена товара может быть определена по формуле:
Данное выражение можно представить в виде мультипликативной модели:
где – доли (удельные веса) объемов продажи, которые характеризуют
структуру продажи данного товара.
Такие индексы образуют индексную систему, которая для качественных показателей состоит из трех элементов: • индексов переменного состава IхПС; • индексов фиксированного (постоянного) состава IхФС; • индексов структурных сдвигов IхCС, где х — вид рассматриваемого признака (цена, себестоимость, производительность труда и т. п.).
Индекс переменного состава IхПС показывает относительное изменение рассматриваемого среднего уровня признака в целом за счет двух факторов — изменения индексируемого признака и изменения в структуре совокупности:
где х1, х0 — средние признаки соответственно в текущем и базисном периодах; f1, f0— веса признака в сопоставляемых периодах.
Индекс фиксированного состава IхФС характеризует изменение среднего уровня за счет изменения только индексируемой величины (соизмерители неизменны) при той же структуре совокупности:
Индекс структурных сдвигов IхСС показывает изменение ср
|
||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 447; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.014 с.) |

 Определить среднюю во многих случаях можно черезисходное соотношение средней (ИСС) или ее логическую формулу:
Определить среднюю во многих случаях можно черезисходное соотношение средней (ИСС) или ее логическую формулу: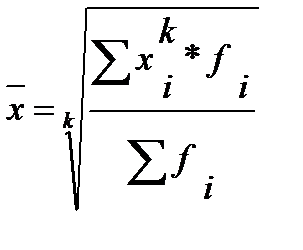
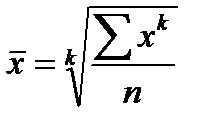

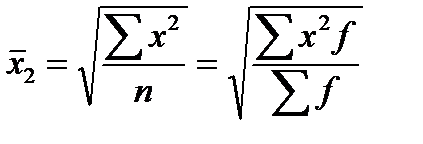
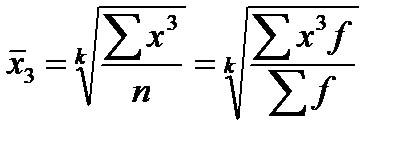
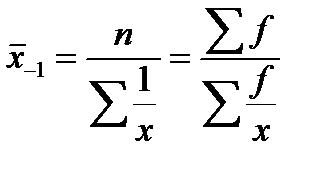
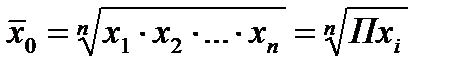
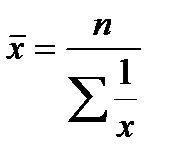

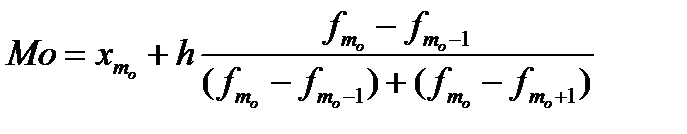
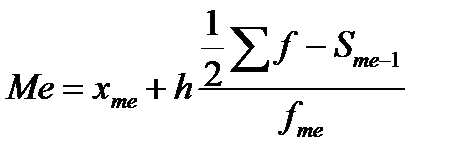


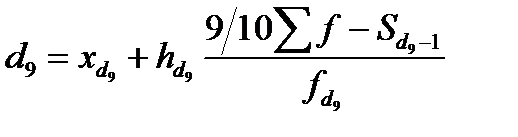

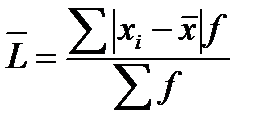
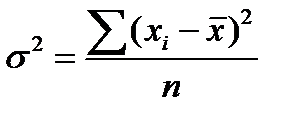

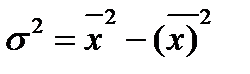 Дисперсия может быть рассчитана как разность средней квадратов вариант и квадрата средней вариант:
Дисперсия может быть рассчитана как разность средней квадратов вариант и квадрата средней вариант: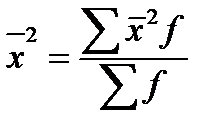
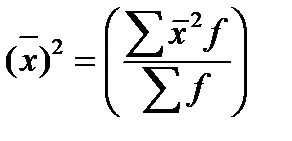
 По равноинтервальному ряду распределения или дискретному ряду с одним и тем же шагом между значениями осредняемого признака возможен расчет дисперсии способом «моментов»:
По равноинтервальному ряду распределения или дискретному ряду с одним и тем же шагом между значениями осредняемого признака возможен расчет дисперсии способом «моментов»: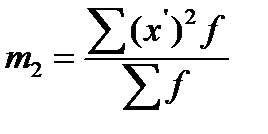
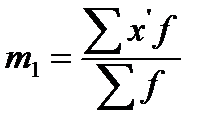
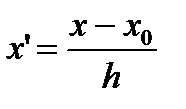
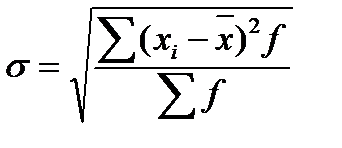
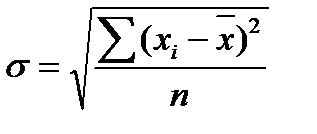
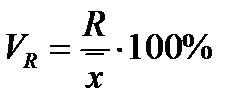 Для осуществления сравнений колеблемости различных признаков в одной и той же совокупности, а также при сопоставлении признака в нескольких совокупностях с разными средними арифметическими используются также относительные показатели вариации (по отношению к среднему значению признака):
Для осуществления сравнений колеблемости различных признаков в одной и той же совокупности, а также при сопоставлении признака в нескольких совокупностях с разными средними арифметическими используются также относительные показатели вариации (по отношению к среднему значению признака): Коэффициент осцилляции (VR) (колеблемость крайних значений признака вокруг средней):
Коэффициент осцилляции (VR) (колеблемость крайних значений признака вокруг средней):


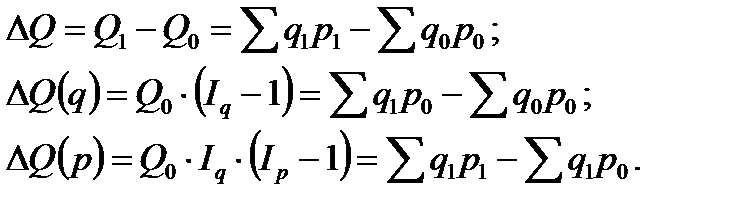
 Средний арифметический индекс физического объема продукции вычисляется по формуле:
Средний арифметический индекс физического объема продукции вычисляется по формуле: