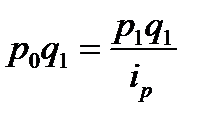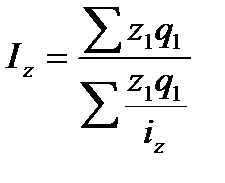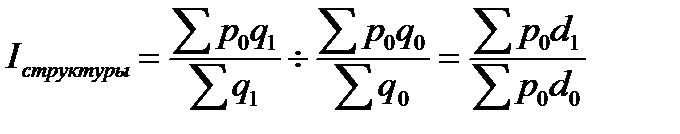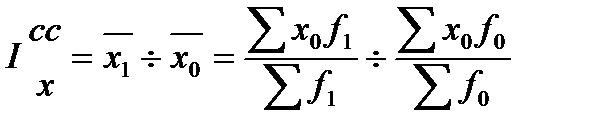Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Виды дисперсий и правило их сложенийСодержание книги
Поиск на нашем сайте
Выделяют дисперсию общую, межгрупповую и внутригрупповую. Общая дисперсия σ2 - измеряет вариацию признака во всей совокупности под влиянием всех факторов, обусловивших эту вариацию. Межгрупповая дисперсия ( δ2х или σ2м/гр) характеризует систематическую вариацию:
Внутригрупповая дисперсия (σ2i) отражает случайную вариацию:
Существует закон, связывающий три вида дисперсии. Общая дисперсия равна сумме средней из внутригрупповых и межгрупповой дисперсий
В статистическом анализе широко используется показатель, представляющий собой долю межгрупповой дисперсии в общей дисперсии. Он носит название эмпирического коэффициента детерминации (η2 – «эта»):
Если извлечь корень квадратный из эмпирического коэффициента детерминации, то получим эмпирическое корреляционное отношение (изменяется от 0-1).
Вариация альтернативного признака
Вариация альтернативного признака количественно проявляется в значении нуля у единиц.
Наряду с вариацией количественных признаков может наблюдаться и вариация качественных признаков. Такое изучение вариации достигается, как и для долей количественных признаков, посредством вычисления и анализа следующих видов дисперсий. Внутригрупповая дисперсия доли определяется по формуле
Средняя из внутригрупповых дисперсий рассчитывается так:
Формула межгрупповой дисперсии имеет следующий вид:
р – доля изучаемого признака во всей совокупности, которая определяется по формуле:
Общая дисперсия определяется по формуле
Индексы Общее понятие об индексах. Классификация индексов. Индивидуальные индексы. Агрегатная форма общих (сводных) индексов. Система индексов. Средневзвешенные индексы. Сводные индексы средних величин. Индексный анализ территориальных различий.
Индекс (с лат.) — указатель или показатель.
В статистике индексом называют показатель относительного изменения данного уровня исследуемого явления по сравнению с другим его уровнем, принятым за базу сравнения. В качестве такой базы может быть использован уровень за какой-либо прошлый период времени (динамический индекс) или уровень того же явления по другой территории (территориальный индекс).
Индекс характеризует изменение социально-экономических явлений во времени, пространстве или по сравнению с планом, стандартом, эталоном, нормой.
Индексы всегда характеризуются отношением одноименных понятий: цена, себестоимость, производительность труда и т.д.
Индексный метод – методология построения и использования индексов в статико-экономическом анализе.
Есть синтетические и аналитические свойства. Синтетические свойства – с помощью индексов осуществляется соединение в единое целое разнородных единиц статистической совокупности. Аналитические свойства – выявляется влияние отдельных факторов на изменение исследуемого показателя.
Условные обозначения: · Количественные или качественные q - объем изготовленной продукции или количество проданного товара опреленного вила в натуральном выражении; T - общее количество отработанных человеко-часов или человеко-дней, среднесписочная численность рабочих; h или s - размер посевной площади. · Качественные показатели p - цена единицы товара или продукции; z - себестоимость единицы продукции; - расходы рабочего времени (труда) на производство продукции, т.е. ее трудоемкость; - средний выпуск продукции в расчете на одного работника или на один человеко-день, т.е. производительность труда; - урожайность определенной культуры с 1 га.
Индексируемая величина – величина, изменение которой изучают при использовании индивидуальных и общих индексов. Соизмеритель – величина, которая приводит разнородные элементы совокупности к сопоставимому виду.
Классификация индексов Индексы могут быть классифицированы по таким признакам: а)мера охвата элементов совокупности: индивидуальные – относительные показатели, которые характеризуют изменения в динамике или отображают соотношение в пространства какого-либо одного вида единиц явления; общие – позволяют соединить разнородные явления, те явления, которые нельзя сложить ни во времени, ни в пространстве. б)база сравнения: базисные, цепные. в)вид объекта сравнения: динамические, территориальные, индексы сопоставления с планом. г)вид соизмерителя: постоянные, переменные соизмерители. д)форма построения: агрегатные, средние. ж) в зависимости от содержания и характера индексируемой величины: количественные, качественные. з) объект исследования: индексы физического объема продукции, производительности труда, стоимости продукции, индексы размера и структуры посевных площадей. к) состав явления: постоянного состава (изменяется одна величина), переменного состава (две и более величины), структурных сдвигов (отношение переменного состава к индексу постоянного состава). л) период расчета.
Индивидуальные индексы
Простейшим показателем, используемым в индексном анализе, является индивидуальный индекс, который характеризует изменение во времени экономических величин, относящихся к одному объекту (или однотоварных явлений). Примерами индивидуальных индексов являются такие:
Взаимосвязь между цепными и базисными индивидуальными индексами: произведение цепных индексов равняется базисному индексу крайних периодов; частное от деления последующего базисного индекса на предыдущий равняется соответствующему цепному индексу.
Агрегатная форма общего индекса. Сущность и принципы построения Агрегатные индексы являются основной формой общего индекса (от лат. aggrega — присоединяю). Свое название они получили потому, что характеризуют не отдельные единицы, а их группы (агрегаты). Одной из первых попыток агрегировать в индексе различные единицы совокупности можно считать формулу индекса цен французского экономиста Дюто, предложенную в 1738 г.:
где ∑p1 – сумма цен на отдельные товары в отчетном периоде; ∑p0 – сумма цен на те же товары в базисном периоде.
Д/З: Средняя часовая выработка рабочего в 3 квартале по сравнению со 2 выросла на 5%. Средняя фактическая продолжительность рабочего дня снизилась на 0,6%. Среднее число дней работы одного рабочего увеличилось на 1,7%. Доля численности рабочих в общей численности работающих возросла на 3%. Найти индивидуальные индексы. Найти индекс квартальной выработки работающего (выработка 1,05; 0,994; 1,107 = 1,0614)
В 1764г. Карли определил общий индекс цен как среднюю арифметическую простую из индивидуальных цен. Базисная цена в качестве соизмерителя была предложена в агрегатной форме индекса Ласпейресом в 1864г. В отечественной практике для расчета индекса количественного показателя чаще используют формулу Ласпейреса, качественного – Пааше.
Индекс физического объема продукции – наиболее типичный общий индекс количественных показателей. Изменение цен на продукции в текущем периоде по сравнению с базисным не влияет на величину индекса. Если объектом исследования является отдельное предприятие, то индекс определяется по совокупности произведенных товаров. Когда объект исследования – отрасль, то складываем совокупности всех произведенных товаров в отрасли. Если объектом исследования является регион, то индекс рассчитывается по всем предприятием региона. Индекс физического объема показывает во сколько раз возросла/уменьшилась стоимость продукции из-за роста/снижения объема его производства. Разность между числителем и знаменателем индекса показывает на сколько рублей изменилась стоимость продукции в результате роста/уменьшения ее объема.
Обозначения: • q1 – количество одноименных единиц продукции (объем продаж одноименного товара) в отчетном периоде; • q0 — количество одноименных единиц продукции (объем продаж одноименного товаpа) в базисном периоде; • р0 — цена одноименной единицы продукции (товара) в базисном периоде; • z0 — себестоимость одноименной единицы продукции в базисном периоде; • q1 p0 – стоимость выпуска одноименной продукции отчетного периода в ценах базисного периода(товарооборот одноименного товара отчетного периода в ценахбазисного периода); • q0 p0 – стоимость выпуска одноименной продукции в базисном периоде (товарооборот одноименного товарав базисном периоде); • ∑q1 p0 – стоимость выпуска разноименной продукции отчетного периода в ценах базисного периода (товарооборот разноименного товара отчетного периода в ценах базисного периода); • ∑q0 p0 – стоимость выпуска разноименной продукции в базисном периоде (товарооборот разноименных товаров в базисном периоде);
Индексы цен нужны для технико-экономических обоснований в проектном строительстве, при пересчете основных показателей Системы Национальных Счетов.
В настоящее время остается проблема подбора универсального соизмерителя в агрегатных индексах цен. Индексы цен рассчитываются не по всей совокупности продукции, а по тем продуктам, которые составляю товарную корзину. Поэтому товарная корзина в разных странах различна. В меньшей степени показывают в общем произведенную продукцию.
Индекс потребительских цен – универсальный измеритель. Он служит для пересмотра социальных программ, расчета минимальной заработной платы. Отражает реальную покупательную способность денег.
Методология расчета данного индекса: 1. Отбор товаров, услуг, представителей и торговых предприятий, по которым производится регистрация цен. 2. Формирование структуры весов по отдельным группам товаров и услуг для расчета сводного индекса потребительских цен. Для формирования структуры весов используются данные о структуре потребительских расходов населения. 3. Методология расчета потребительских цен предполагает, что индекс рассчитывается отдельно для регионов, товарных групп и отдельных групп населения.
Для индексов стоимостных показателей соизмерителей не требуется, достаточно произвести суммирование произведений качественного и количественного показателей.
Для взвешивания качественного показателя используется средний объем, то общий индекс называется индексом Лоу. Применяется когда нужно сделать расчеты за очень длительный период. Система индексов
Индексы позволяют получать сводную оценку изучаемых процессов постоянно, месяц за месяцем, год за годом. Однако при этом для достижения сопоставимости они должны рассчитываться по единой методологии. Такая методология или схема расчета индексом за несколько последовательных временных периодов называется системой индексов.
В зависимости от информационной базы и целей исследования индексная система может строиться по-разному. При этом используются цепные и базисные способы расчета.
Для индексов с постоянными соизмерителями: произведение цепных индексов равняется базисному индексу крайних периодов; частное от деления последующего базисного индекса с постоянными соизмерителями на предыдущий равняется цепному индексу.
Данные индексы с постоянными весами предпочтительнее потому что они мультипликативны по своей сущности, т.е. их можно последовательно перемножать.
Цепные индексы цен с переменными весами, с постоянными весами.
Система базисных индексов с переменными весами, с постоянными весами.
С помощью индексов можно определить абсолютный прирост итогового показателя мультипликативной модели, как в целом, так и по факторам этой модели. Для модели товарооборота:
Средневзвешенные индексы
Существуют две формы средневзвешенных индексов: • Среднеарифметическая. • Среднегармоническая. Как правило, средний арифметический индекс применяется при индексации количественных показателей (например, физического объема продукции), а средний гармонический — при индексации качественных показателей (например, цен).
Весами в формуле является стоимость продукции базисного периода. Так как iq х q0 = q1, то формула этого индекса легко преобразуется в формулу:
Средний арифметический индекс производительности труда определяется следующим образом:
Так как itх t1, = t0, то формула этого индекса может быть преобразована в агрегатный индекс трудоемкости продукции. Весами являются общие затраты времени на производство продукции в текущем периоде.
В статистике широко известен и другой средний арифметический индекс, который используется при анализе производительности труда. Он носит название индекса Струмилина.
Индексы других качественных показателей (цен, себестоимости и т. д.) определяются по формуле средней гармонической взвешенной величины.
Средний гармонический индекс тождествен агрегатному, если индивидуальные индексы будут взвешены с помощью слагаемых числителя агрегатного индекса. Тогда при расчете сводного индекса цен по методу Паше можно использовать следующую замену:
Сводный индекс цен будет выражен в форме сред ей гармонической,
а инд екс себестоимости можно исчислить так:
Общие (сводные) индексы средних величин
В экономико-статистическом анализе приходится сравнивать в динамике такие обобщающие характеристики качественных показателей как • средняя цена, • средняя себестоимость, • средняя производительность труда • средняя заработная плата и др.
Показывают изменение среднего значения индексируемого показателя. Применяются только для качественных показателей. Индексы средних величин применяются при обобщении данных не по элементам, а по единицам совокупности. Например: цена товара одного вида (элемента), продаваемого в разных торговых точках обобщается в виде средней (по предприятиям торговли) цены этого товара; себестоимость одного вида продукции обобщается в виде средней себестоимости данной продукции по совокупности производящих ее предприятий (т. е. по единицам совокупности). Средняя цена товара может быть определена по формуле:
Данное выражение можно представить в виде мультипликативной модели:
где – доли (удельные веса) объемов продажи, которые характеризуют
структуру продажи данного товара.
Такие индексы образуют индексную систему, которая для качественных показателей состоит из трех элементов: • индексов переменного состава IхПС; • индексов фиксированного (постоянного) состава IхФС; • индексов структурных сдвигов IхCС, где х — вид рассматриваемого признака (цена, себестоимость, производительность труда и т. п.).
Индекс переменного состава IхПС показывает относительное изменение рассматриваемого среднего уровня признака в целом за счет двух факторов — изменения индексируемого признака и изменения в структуре совокупности:
где х1, х0 — средние признаки соответственно в текущем и базисном периодах; f1, f0— веса признака в сопоставляемых периодах.
Индекс фиксированного состава IхФС характеризует изменение среднего уровня за счет изменения только индексируемой величины (соизмерители неизменны) при той же структуре совокупности:
Индекс структурных сдвигов IхСС показывает изменение среднего уровня за счет изменений в структуре совокупности при неизменном значении признака:
IxПС = Ix ФС *IxСС
Абсолютные изменения средней цены в целом и по факторам определяются формулами:
IxПС
Ix ФС
IxСС
Очевидно, справедливо соотношение:
|
||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 158; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.211.246 (0.009 с.) |

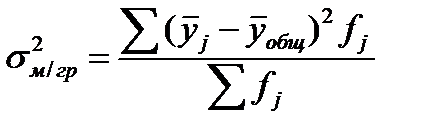
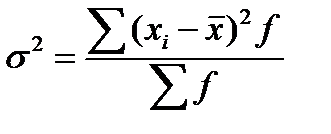
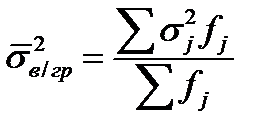 Правило сложения дисперсий широко применяется при исчислении показателей тесноты связи, в дисперсионном анализе, при оценке точности типической выборки и в ряде других случаев.
Правило сложения дисперсий широко применяется при исчислении показателей тесноты связи, в дисперсионном анализе, при оценке точности типической выборки и в ряде других случаев.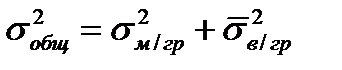
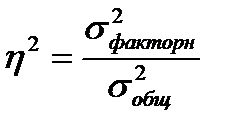
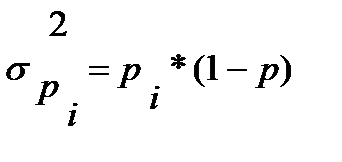
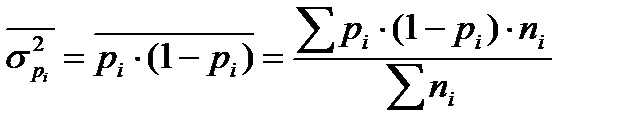
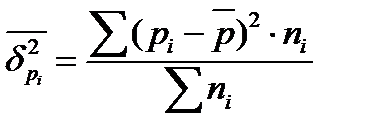
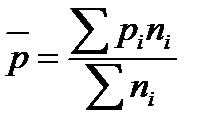
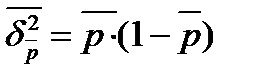
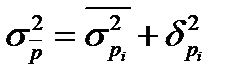 Три вида дисперсии связаны между собой следующим образом:
Три вида дисперсии связаны между собой следующим образом:
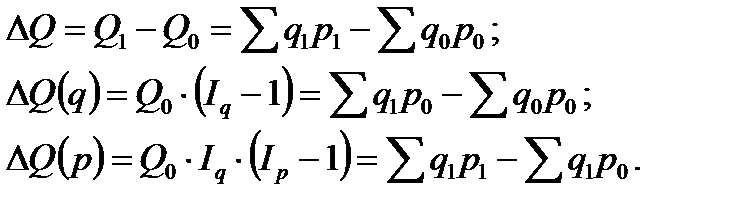
 Средний арифметический индекс физического объема продукции вычисляется по формуле:
Средний арифметический индекс физического объема продукции вычисляется по формуле: