
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие о вариации, необх-ть и задачи стат. Изучения вариацииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Вариация - изменение признака (вариант) в стат. совокупности, т.е. принятие единицами совокупности или их группами разных значений признака. Вариация присуща всем явлениям окруж. жизни (природы, общества). Природа вариации любого признака чрезвычайно сложна, т.к. на его изменение оказывает влияние множество факторов. Н-р, колебания урожайности ржи обусловлены многочисленными причинами, которые сосредоточены в природных, технол. и эк. условиях фор-ния этой урож-ти. Физ., хим.е, биолог., биохимич. и др. формы движения всех явлений окруж. мира могут проявляться во взаимодействии, либо переходят друг в друга, что и порождает вариацию любого признака в каждой статист. ед-це и совок-сти в целом. Вариация, как результат взаимодействия различных форм движения – это база для постоянного и бесконечного совершенствования явлений. Присуща всем явлениям, к-рые изменяются качест. и колич. во времени и пространстве. Вариация признаков в пространстве - это колич. различие любого признака по каждой единице статист. совок-сти за один и тот же период или по состоянию на один и тот же момент времени. Н-р, вариация урож-сти ржи на разл. посев. уч-ках в 2010 г. Cуществует также вариация во времени. Под ней подразумевают изменение значений признака в различные периоды (или моменты) времени. Так, со временем изменяются средняя продолжительность жизни, срок службы товаров длительного пользования, и т. д. Именно вариация предопределяет необходимость использования статистики. В тех случаях, где имеют место "неварьирующие" признаки, необходимость в статистике отпадает. При качеств. харак-ке явлений статист. признаки могут принимать одно из двух противоположных значений. В таких случаях вариация признается альтернативной. Н-р, рабочий квалифицированный — неквалиф-ный. Если вариация признака идет в определенном направлении, но изменение не обусловлено внутренним законом развития явления, то ее принято называть систематической; если же вариация не имеет явно выраженного направления, то ее называют случайной. Примером систематической вариации может быть колебание годового удоя коров под воздействием только породы; случайной вариации удоя – под воздействием каких – либо иных факторов.
Наличие вариации в признаках изучаемых явлений ставит перед статистикой задачи ее исследования: 1) определение меры вариации и ее измерение, 2) нахождение соответствующих измерителей и показателей, характеризующих размеры вариации, 3) выявление сущности показателей вариации и методов вычисления факторов, ее определяющих. По степени вариации можно судить о многих сторонах процесса развития изучаемых явлений, в частности об однородности совокупности, устойчивости индивидуальных значений признака, типичности средней, о взаимосвязи между признаками одного и того же явления и признаками разных явлений.
22. Абсолютные и относительные харак-к измерения вариации. Основные матем. св-ва дисперсии. Показатели вариации делятся на две группы: абсолютные и относительные. К абсолютным отн-ся размах вариации, cpeднее линейное отклонение, дисперсия и среднее квадратическое отклонение. Вторая группа показателей вычисляется как отношение абсолютных показателей вариации к средней арифметической (или медиане). Относительными показателями вариации являются коэф-ты осцилляции, вариации, относительное линейное отклонение и др. Простейшим показателем вариации признака является вариационный размах. Вариационный размах (амплитуда колебаний) признака рассчитывается как разность между макс-ной и миним-ной вариантами опред. колич-ного признака в статист. совокупности. Вариационный размах рассчитывают:
где Rх – размах вариации признака;
Основной недостаток вариационного размаха заключается в том, что он не отражает внутренних изменений признака и полностью зависит от отдельных случаев, оказывающихся на обоих полюсах ранжированного ряда. Для приближенной обобщающей харак-ки вариации признака может быть рассчитано среднее линейное отклонение, которое выражается в простой и взвешенной формах. Поскольку матем. сумма линейных отклонений (Σ Простое среднее линейное отклонение, рассчитываемое для ранжированного ряда, находят следующим образом:
где Взвешенное среднее линейное отклонение, которое может быть найдено для дискретного или интервального ряда распределения, рассчитывают по следующей формуле:
Среднее линейное отклонение, как один из простейших показателей, находит ограниченное применение; главным образом может быть использовано лишь для приближенной характеристики внутренних колебаний вариационного признака в статистической совокупности, так как оно рассчитывается с нарушением математических правил. Поэтому для более точной и объективной оценки внутренних изменений основными показателями вариации являются следующие: среднее квадратической отклонение и коэффициент вариации. Дисперсия признака
и взвешенной средней арифметической
Существуют более простые подходы в вычислении дисперсии. Наиболее часто используется сокращенный способ расчета дисперсии (метод моментов), в соответствии с которым дисперсия
Этот способ позволяет вести расчет дисперсии по исходным данным без предварительного расчета отклонений. Дисперсия как базовый показатель вариации обладает рядом вычислительных свойств, позволяющих упростить её расчет. К ним относятся: 1. дисперсия постоянной величины равна 0; 2. дисперсия не меняется, если все варианты увеличить или уменьшить на одно и то же число А; 3. если все варианты умножить (разделить) на число А, то дисперсия увеличится (уменьшится) в квадрат постоянного числа A2. Размерность дисперсии соответствует квадрату размерности исследуемого признака, поэтому данный показатель не имеет экономической интерпретации. Для сохранения экономического смысла рассчитывается ещё один показатель вариации – среднее квадратическое отклонение. Среднее квадратическое отклонение рассчитывается на базе средней квадратической величины. Оно выступает в невзвешенной (простой) и взвешенной формах. Для ранжированного ряда рассчитывают невзвешенное (простое) среднее квадратическое отклонение по следующей формуле: простая – Взвешенное среднее квадратическое отклонение рассчитывают для дискретного или интервального ряда: взвешенная – Среднее квадратическое отклонение измеряется в тех же единицах, что и варианты изучаемого признака в статистической совокупности. Оно харак-ет среднюю колеблемость вариант в этой совокупности и широко используется в качестве одного из наиболее точных и объективных показателей вариации не только в статистике, но и в технике, биологии, других отраслях знаний. Для целей сравнения колеблемости различных признаков в одной и той же совокупности или же при сравнении колеблемости одного и того же признака в нескольких совокупностях используют показатели вариации, приведенные в относительных величинах. Базой для сравнения должна служить средняя арифметическая. Эти показатели вычисляются как отношение размаха вариации, среднего линейного отклонения или среднего квадратического отклонения к средней арифметической или медиане. Чаще всего они выражаются в процентах и определяют не только сравнительную оценку вариации, но и дают характеристику однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33% (для распределений, близких к нормальному). Различают следующие относительные показатели вариации:
Коэффициент осцилляции (
где Vх – коэффициент вариации признака х в статистической совокупности;
Базой для расчёта коэффициента вариации может быть не только средняя величина, но и заменяющие её величины (например, мода и медиана). Обычно коэффициент вариации выражают в процентах и используют как объективную меру колеблемости вариант в статистической совокупности. В этом случае коэффициент вариации может характеризовать количественную однородность или разнородность изучаемых признаков в составе статистической совокупности. Если же коэффициент вариации выше 10,0%, то статистическая совокупность по заданному признаку считается неоднородной. Коэффициент вариации может быть использован при сравнении колеблемости нескольких признаков как в одной и той же статистической совокупности, так и в различных совокупностях. Н-р, с пом. коэффициента вариации можно сравнить колеблемость урожайности различных с.х. культур, продуктивности животных в различных категориях хозяйств и др.
|
|||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 1104; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.180.88 (0.012 с.) |


 – соответственно конечная (максимальная) и начальная (минимальная) варианты.
– соответственно конечная (максимальная) и начальная (минимальная) варианты. ), согласно первому свойству средней арифметической величины, всегда =0, то для расчета среднего линейного отклонения берут сумму линейных отклонений по модулю.
), согласно первому свойству средней арифметической величины, всегда =0, то для расчета среднего линейного отклонения берут сумму линейных отклонений по модулю.

 – среднее линейное отклонение;
– среднее линейное отклонение;  – линейное отклонение индивидуальных вариант от их среднего
– линейное отклонение индивидуальных вариант от их среднего  ; n – число вариант в статистической совокупности.
; n – число вариант в статистической совокупности.
 представляет собой средний квадрат отклонений вариантов от их средней величины, является общепринятой мерой вариации. В зависимости от исходных данных дисперсия вычисляется по формулам простой:
представляет собой средний квадрат отклонений вариантов от их средней величины, является общепринятой мерой вариации. В зависимости от исходных данных дисперсия вычисляется по формулам простой:
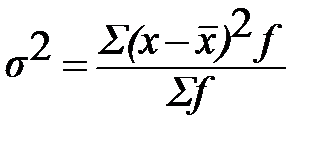
 есть разница между средним из квадратов значений признака
есть разница между средним из квадратов значений признака  и квадратом их средней (
и квадратом их средней ( ):
):

 ;
; .
. ):
): Коэффициент вариации представляет собой относительный показатель, который можно рассчитать по следующей формуле:
Коэффициент вариации представляет собой относительный показатель, который можно рассчитать по следующей формуле:
 – среднее квадратическое отклонение признака х;
– среднее квадратическое отклонение признака х; – среднее значение признака в статистической совокупности.
– среднее значение признака в статистической совокупности.


