
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Абсолютные и средние показатели вариации.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Наиболее простой показатель вариации - размах вариации, определяемый как разность между наибольшим (xmax) и наименьшим (xmin) значениями вариант R = xmax - xmin Этот показатель прост в вычислении и указывает на общие размеры вариации, но он не дает представления о степени колеблемости внутри совокупности, т.к. улавливает только крайние отклонения. Различие всех единиц изучаемой совокупности учитывает среднее линейное отклонение. Среднее линейное отклонение есть средняя арифметическая из отклонений индивидуальных значений от средней (без учета знака этих отклонений):
или На практике меру вариации более объективно отражает показатель дисперсии. Дисперсия – это средняя арифметическая квадратов отклонений каждого значения признака от средней арифметической. Другими словами, это средний квадрат отклонений. Дисперсия вычисляется по формуле:
или Корень квадратный из дисперсии представляет собой среднее квадратическое отклонение. Достоинством этого показателя является то, что он выражается в тех же единицах измерения, что и признак.
или Дисперсия и среднее квадратическое отклонение являются основными обобщающими показателями вариации. Среднее квадратическое отклонение является мерилом надежности средней. Чем меньше этот показатель, тем лучше средняя арифметическая отражает всю представляемую совокупность. Относительные показатели вариации Относительные показатели вариации позволяют сравнивать характер рассеивания в различных совокупностях, например, при сравнении разноименных совокупностей, при различных значениях средней. Расчет относительных показателей вариации осуществляют как отношение абсолютного показателя вариации к средней арифметической. Как правило, они рассчитываются в процентах. Коэффициент осцилляции отражает относительную колеблемость крайних значений вокруг средней
Линейный коэффициент вариации характеризует долю усредненного значения абсолютных отклонений от средней величины
Коэффициент вариации – наиболее распространенный показатель колеблемости, используемый для оценки типичности средней.
Чем больше разброс значений признака вокруг средней, тем больше коэффициент вариации и тем менее представительна средняя. Как правило, считают, что если Правило сложения дисперсий Определить влияние отдельных факторов, характеризующих колеблемость индивидуальных значений признака можно при помощи группировок, подразделив изучаемую совокупность на группы, однородные по изучаемому признаку. При этом можно исчислить следующие виды дисперсий: общую дисперсию, внутригрупповые дисперсии, среднюю из внутригрупповых дисперсий и межгрупповую дисперсию. Внутригрупповые дисперсии (σ1, σ2, …) отражают случайную вариацию, т.е. часть вариации, происходящую влиянием неучтенных факторов и не зависящую от признака-фактора, положенного в основание группировки. Средняя из внутригрупповых дисперсий ( Межгрупповая дисперсия (
Общая дисперсия ( Между указанными видами дисперсий существует соотношение: общая дисперсия равна сумме величин средней из внутригрупповых дисперсий и межгрупповой дисперсии. Формула правила сложения дисперсий:
Правило сложения дисперсий позволяет выявить зависимость результативного признака от определяющих факторов путем соотношения межгрупповой и общей дисперсии:
Здесь
|
||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 553; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.170 (0.006 с.) |







 .
.
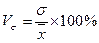
 >33%, то это говорит о большой колеблемости признака в совокупности, и совокупность неоднородна.
>33%, то это говорит о большой колеблемости признака в совокупности, и совокупность неоднородна. ) – это средняя арифметическая взвешенная из внутригрупповых дисперсий.
) – это средняя арифметическая взвешенная из внутригрупповых дисперсий. ) – это средний квадрат отклонений групповых средних от общей средней. Характеризует систематическую вариацию, т.е. различия в величине изучаемого (результативного) признака за счет признака-фактора, положенного в основание группировки.
) – это средний квадрат отклонений групповых средних от общей средней. Характеризует систематическую вариацию, т.е. различия в величине изучаемого (результативного) признака за счет признака-фактора, положенного в основание группировки.
 ) характеризует вариацию признака, которая зависит от всех условий в данной совокупности.
) характеризует вариацию признака, которая зависит от всех условий в данной совокупности.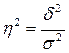
 - коэффициент детерминации, который показывает долю вариации результативного признака, объясненную влиянием вариации факторного признака.
- коэффициент детерминации, который показывает долю вариации результативного признака, объясненную влиянием вариации факторного признака.


