Статистическое изучение связи

Основные понятия и предпосылки корреляционно-регрессионного анализа

Большинство статистических исследований ставит своей целью выявление взаимозависимостей меду признаками. Все статистические методы прогнозирования базируются на факте существования таких зависимостей, иначе прогноз стал бы невозможным. Признаки по их значению для изучения взаимосвязи делятся на два класса: факторные, или факторы – признаки, обуславливающие изменения других, связанных с ними, признаков, и результативные – признаки, изменяющиеся под действием факторных признаков.

Между общественными явлениями существует два типа связи: функциональная и корреляционная.

При функциональной связи изменение независимых переменных приводит к получению точно определенных значений зависимой переменной.

Корреляционной связью называется важнейший частный случай статистической связи, состоящий в том, что разным значениям одной переменной соответствуют различные средние значения другой переменной. В статистике принято различать следующие варианты зависимостей:

1. парная корреляция – связь между двумя признаками (результативным и факторным или двумя факторными)

2. частная корреляция – зависимость между результативным и одним факторным признаками при фиксированном значении других факторных признаков.

3. множественная корреляция – зависимость результативного и двух или более факторных признаков, включенных в исследование

По направлению различают прямую связь, при которой с увеличением (уменьшением) значений факторного признака происходит увеличение (уменьшение) значений результативного, и обратную связь, при которой значения факторного признака изменяются под воздействием факторного в противоположном направлении.

Корреляционно-регрессионный анализ как общее понятие включает в себя измерение тесноты, направления связи и установление аналитической формы связи. Корреляционный анализ имеет своей задачей количественное определение тесноты связи между двумя признаками (при парной связи) и между результативным и множеством факторных признаков (при многофакторной связи). Регрессионный анализ заключается в определении аналитического выражения связи, в котором изменение результативного признака обусловлено влиянием одного или нескольких факторов, а множество всех прочих факторов, также оказывающих влияние на зависимую величину, принимается за постоянные и средние значения. Корреляция и регрессия тесно связаны между собой: первая оценивает силу статистической связи, вторая исследует ее форму.

Предпосылки корреляционно-регрессионного анализа.

1. Наличие данных по достаточно большой совокупности явлений. Это общее условие всякого статистического исследования. Обычно считается, что число наблюдений должно быть в 5-6 (а лучше – не менее чем в 10 раз) больше числа факторов. Большое число наблюдений позволяет закону больших чисел, действуя в полную силу, обеспечить эффективное взаимопогашение случайных отклонений от закономерного характера связи признаков.

2. Качественная однородность тех единиц, которые подвергаются изучению методами корреляционно-регрессионного анализа.

3. При выполнении вышеуказанных требований далее необходимо провести количественную оценку однородности исследуемой совокупности по комплексу признаков. Одним из возможных вариантов такой оценки является расчет относительных показателей вариации (традиционно широкое применение для этих целей получил коэффициент вариации).

4. При ограничении числа факторов, вводимых в модель, наряду с качественным анализом целесообразно использовать и количественные оценки, позволяющие конкретно охарактеризовать влияние факторов на результативный показатель. Включаемые в исследование факторы должны быть независимы друг от друга, так как наличие тесной связи между ними свидетельствует о том, что они характеризуют одни и те же стороны изучаемого явления и дублируют друг друга.

5. Целесообразным является изучение формы распределения исследуемых признаков, т.к. все основные положения теории корреляции разрабатывались применительно к предположению о нормальном характере распределения исследуемых признаков. Это условие связано с применением метода наименьших квадратов (МНК) при расчете параметров корреляции: только при нормальном распределении МНК дает оценку параметров, отвечающую принципам максимального правдоподобия. На практике эта предпосылка выполняется приближенно. Однако при значительном отклонении распределения признаков от нормального закона возникают проблемы с оценкой надежности рассчитанных по выборочным данным коэффициентов корреляции.

В соответствии с сущностью корреляционной связи ее изучение имеет две цели:

1. измерение тесноты связи двух или более признаков между собой

2. измерение параметров уравнения, выражающего зависимость средних величин результативного признака от значений одного или нескольких факторных признаков;

Измерение степени тесноты корреляционной связи

В случае парной зависимости

Показатели тесноты связи используются для решения следующих задач:

1. Вопрос о необходимости изучения данной связи и целесообразности ее практического применения.

2. Вопрос о степени различий тесноты связи для конкретных условий.

3. Для выявления решающих факторов, воздействующих главным образом на формирование величины результативного признака.

Теснота связи при линейной зависимости измеряется с помощью линейного коэффициента корреляции Пирсона:

Значение линейного коэффициента корреляции важно для исследования социально-экономических явлений и процессов, распределение которых близко к к нормальному. Он принимает значения в интервале –1 ≤ r ≤ 1. Отрицательные значения указывают на обратную связь, положительные – прямую. При r=0 линейная связь отсутствует. Чем ближе r по абсолютной величине к 1, тем теснее связь между признаками. При r= 1 связь функциональная.

Квадрат коэффициента корреляции r² представляет собой коэффициент детерминации, который показывает долю вариации результативного признака, объясненную влиянием вариации факторного признака.

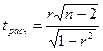Для оценки существенности (значимости) линейного коэффициентакорреляции используется тот факт, что величина при условии отсутствия связи в генеральной совокупности распределена по закону Стьюдента с (n-2) степенями свободы (где n – объем выборки). Полученную t_расч сравнивают табличным значением. Коэффициент корреляции признается значимым при уровне значимости , если t_расч>t_табл. В этом случае практически невероятно, что найденное значение коэффициента корреляции обусловлено только случайными совпадениями. Уровень значимости показывает вероятность принятия ошибочного решения, например, при =0,05 в среднем пяти случаях из ста есть риск сделать ошибочное заключение о значимости коэффициента корреляции (в социально-экономических исследованиях обычно =0,1, =0,05 или =0,01).