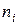Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Построение вариационного рядаСодержание книги
Поиск на нашем сайте Введение
Наука, изучающая закономерности массовых случайных событий, называется теорией вероятностей. Применение теории вероятностей к обработке больших совокупностей чисел называется математической статистикой. Основная задача математической статистики состоит в разработке методов, позволяющих обобщать результаты наблюдений. Статистические совокупности могут быть взяты из самых разнообразных областей, поэтому математическая статистика находит себе применение во всевозможных исследованиях: в физике, астрономии, биологии, метеорологии, демографии, экономике, современном производстве и технике и т.д. Любое статистическое исследование состоит из нескольких основных этапов: 1) организация и планирование статистических наблюдений; 2) сбор статистических данных; 3) анализ статистических данных; 4) принятие решений, рекомендаций и выводов; 5) прогнозирование случайных явлений; 6) статистический контроль регулирования хода технологических процессов, оценка качества партий продукции. Цель методических указаний – формирование навыков статистической обработки экспериментального материала, которые могут быть использованы при выполнении исследовательских работ по различным учебным дисциплинам, при выполнении курсовых работ и дипломном проектировании, в научных исследованиях. Эти навыки будут полезны студентам всех специальностей и различных форм обучения. Задания к РГР: 1. По результатам выборки построить вариационный ряд. 2. Представить графическое изображение вариационного ряда (полигон и гистограмму). 3. Составить эмпирическую функцию распределения и нарисовать ее график. 4. Вычислить основные выборочные характеристики. 5. Найти точечные и интервальные оценки параметров распределения. 6. На основе полученных результатов выдвинуть гипотезу о виде распределения (нормальное распределение). 7. С помощью критерия согласия Пирсона проверить гипотезу о нормальном распределении признака генеральной совокупности. 8. Построить эмпирическую кривую распределения. Основные понятия математической статистики
Генеральной совокупностью называется совокупность всех наблюдений, которые могли быть сделаны при данном реальном комплексе условий измерений. Число членов, образующих генеральную совокупность, называется объемом генеральной совокупности N. Генеральная совокупность является понятием модельным. Говоря о распределении случайной величины X в генеральной совокупности, мы можем делать различные предположения о функции распределения Выборочной совокупностью или просто выборкой объема n называется совокупность n объектов, отобранных из исследуемой генеральной совокупности. Пусть имеется выборка результатов испытаний.
В данном примере объем выборки n =100. Для того чтобы суждения о законах распределения случайной величины X или об их числовых характеристиках были объективны, необходимо, чтобы выборка была представительной (репрезентативной), т.е. достаточно хорошо представляла исследуемую случайную величину. В силу закона больших чисел можно утверждать, что выборка будет репрезентативной, если ее осуществить случайно: каждый объект выборки отобран случайно из генеральной совокупности, если все объекты имеют одинаковую вероятность попасть в выборку. Выборка считается большой, если ее объем n >30. Показатели рассеяния Для характеристики отклонения значений признака от среднего арифметического используются: 1) Дисперсия определяется по формуле:
В нашем случае:
2) Среднее квадратическое отклонение определяется по формуле:
В нашем случае: 3) В качестве относительной характеристики рассеяния используют коэффициент вариации, который показывает, насколько велико рассеяние значений по сравнению со средней арифметической. Коэффициент вариации определяется по формуле: В отличие от дисперсии и среднего квадратического отклонения коэффициент вариации – величина безразмерная, что позволяет сравнивать изменчивость признаков как в пределах одной совокупности, так и разных совокупностей, независимо от единиц измерения разных сопоставляемых признаков. Совокупность считается однородной, если коэффициент вариации не превышает 33 % (для распределений, близких к нормальному). Исходя из величины коэффициента вариации, можно установить характеристику изменчивости, например, по следующей схеме:
В нашем случае:
Изменчивость умеренная, совокупность однородна. Предварительный выбор закона распределения
Большинство применяемых в практике контроля статистических методов основано на предложении, что распределение контролируемого признака подчиняется определенному теоретическому закону (нормальному, биноминальному, пуассоновскому и так далее) с параметрами, либо оцениваемыми по выборке, либо заранее известными. Применению этих методов должна предшествовать проверка по данным выборочных наблюдений гипотезы о законе распределения. Проверка гипотезы о законе распределения значения признака Чаще всего на практике имеют дело с нормальным распределением. Чем это объясняется? Ответ на этот вопрос дан А.М.Ляпуновым в центральной предельной теореме теории вероятности. Приведем следствие из нее: если случайная величина Функция плотности нормального закона распределения имеет вид У нормального распределения два параметра (количество параметров Кривая нормального распределения симметрична относительно прямой
1) Для нормального закона средняя арифметическая
У нас: Как видно, значения этих величин практически не отличаются друг от друга. 2) У кривой нормального распределения коэффициенты асимметрии и эксцесса равны нулю. У нас: Как видно, значение коэффициента асимметрии и значение коэффициента эксцесса отличаются от нуля. (Замечание: считается, что число 3) В случае нормального распределения справедливо следующее условие:
Проверим выполнение этого условия для нашего примера.
Условия выполняется. 4) На практике для выдвижения гипотезы о нормальном распределении используют правило 3-х сигм: если случайная величина распределена нормально, то абсолютная величина её отклонения от математического ожидания не превосходит утроенного среднеквадратического отклонения, т.е. все значения случайной величины должны попасть в интервал:
Рисунок 5. – Правило 3-х сигм. В нашем случае все значения величин попадают в интервал Таким образом, у нас есть основания предположить, что изучаемая случайная величина распределена по нормальному закону (нулевая гипотеза):
где Приложение 1 Таблица значений функции
Приложение 2
Критические точки распределения χ2
ЛИтература
1. Гмурман В.Е. Теория вероятностей и математическая статистика: учеб. пособие для вузов / В.Е. Гмурман. – 12-е изд., перераб. – М.: Высш. образование, 2005. – 479 с. 2. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике: учеб. пособие для вузов / В.Е. Гмурман. - 11-е изд., перераб. - М.: Высш. образование, 2007. - 404 с. 3. Баранова И.М., Часова Н.А. Основы теории вероятностей и математической статистики: учеб. пособие. Ч. 1 Теория вероятностей. / И.М.Баранова [и др.]. – Брянск, 2011. – 140 с. СОДЕРЖАНИЕ
Введение. 4 1. Основные понятия математической статистики. 6 2. Построение вариационного ряда. 7 3. Графическое изображение вариационных рядов. 8 4. Эмпирическая функция распределения. 10 5. Основные выборочные характеристики. 12 6. Точечные и интервальные оценки параметров генеральной совокупности 18 7. Статистическая проверка гипотез. 22 8. Предварительный выбор закона распределения. 25 9. Проверка гипотезы о виде распределения. 28 Приложение 1. 32 Приложение 2. 33 ЛИтература.. 34 Баранова И.М., Часова Н.А.
МАТЕМАТИКА
Статистическая обработка
Методические указания к выполнению расчетно-графической работы для студентов всех направлений подготовки бакалавров
Формат Объем Тираж Заказ
Брянск, Станке Димитрова 3, Редакционно-издательский отдел Отпечатано: Печатный цех БГИТА
Введение
Наука, изучающая закономерности массовых случайных событий, называется теорией вероятностей. Применение теории вероятностей к обработке больших совокупностей чисел называется математической статистикой. Основная задача математической статистики состоит в разработке методов, позволяющих обобщать результаты наблюдений. Статистические совокупности могут быть взяты из самых разнообразных областей, поэтому математическая статистика находит себе применение во всевозможных исследованиях: в физике, астрономии, биологии, метеорологии, демографии, экономике, современном производстве и технике и т.д. Любое статистическое исследование состоит из нескольких основных этапов: 1) организация и планирование статистических наблюдений; 2) сбор статистических данных; 3) анализ статистических данных; 4) принятие решений, рекомендаций и выводов; 5) прогнозирование случайных явлений; 6) статистический контроль регулирования хода технологических процессов, оценка качества партий продукции. Цель методических указаний – формирование навыков статистической обработки экспериментального материала, которые могут быть использованы при выполнении исследовательских работ по различным учебным дисциплинам, при выполнении курсовых работ и дипломном проектировании, в научных исследованиях. Эти навыки будут полезны студентам всех специальностей и различных форм обучения. Задания к РГР: 1. По результатам выборки построить вариационный ряд. 2. Представить графическое изображение вариационного ряда (полигон и гистограмму). 3. Составить эмпирическую функцию распределения и нарисовать ее график. 4. Вычислить основные выборочные характеристики. 5. Найти точечные и интервальные оценки параметров распределения. 6. На основе полученных результатов выдвинуть гипотезу о виде распределения (нормальное распределение). 7. С помощью критерия согласия Пирсона проверить гипотезу о нормальном распределении признака генеральной совокупности. 8. Построить эмпирическую кривую распределения. Основные понятия математической статистики
Генеральной совокупностью называется совокупность всех наблюдений, которые могли быть сделаны при данном реальном комплексе условий измерений. Число членов, образующих генеральную совокупность, называется объемом генеральной совокупности N. Генеральная совокупность является понятием модельным. Говоря о распределении случайной величины X в генеральной совокупности, мы можем делать различные предположения о функции распределения Выборочной совокупностью или просто выборкой объема n называется совокупность n объектов, отобранных из исследуемой генеральной совокупности. Пусть имеется выборка результатов испытаний.
В данном примере объем выборки n =100. Для того чтобы суждения о законах распределения случайной величины X или об их числовых характеристиках были объективны, необходимо, чтобы выборка была представительной (репрезентативной), т.е. достаточно хорошо представляла исследуемую случайную величину. В силу закона больших чисел можно утверждать, что выборка будет репрезентативной, если ее осуществить случайно: каждый объект выборки отобран случайно из генеральной совокупности, если все объекты имеют одинаковую вероятность попасть в выборку. Выборка считается большой, если ее объем n >30. Построение вариационного ряда
Пусть изучается некоторая дискретная или непрерывная случайная величина, закон распределения которой известен. Статистический материал, полученный в результате измерений представляют в виде таблицы, состоящей из двух строк, в первой из которых находятся расположенные в возрастающем порядке значения признаков (для дискретной случайной величины) или интервалов (для непрерывной случайной величины), а во второй – их частота На основе имеющейся выборки составляем интервальный статистический ряд. Для выбора оптимальной длины интервалов h воспользуемся формулой: Для нашего случая: Найдём количество интервалов: Найдём длину интервалов (шаг): Нижнюю границу первого интервала принимаем Зная нижнюю границу первого интервала Проанализируем каждое значение имеющейся выборки на факт попадания в определённый интервал, а число значений, попавших в интервал, запишем в столбец «Частота Найдем середину каждого интервала, используя формулу: Таблица 1.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 586; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.012 с.) |

 случайной величины или о параметрах этой функции.
случайной величины или о параметрах этой функции. .
. .
. .
. 0,89.
0,89.

 .
.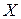 в генеральной совокупности осуществляется с помощью критериев согласия.
в генеральной совокупности осуществляется с помощью критериев согласия. , а интегральная функция распределения –
, а интегральная функция распределения – 
 ): математическое ожидание
): математическое ожидание  и среднее квадратическое отклонение
и среднее квадратическое отклонение 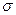 . Их оцениваем по выборке:
. Их оцениваем по выборке:  .
. .
.
 , мода
, мода 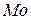 и медиана
и медиана 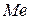 равны как характеристики центра распределения:
равны как характеристики центра распределения: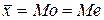
 9,0548;
9,0548;  9,115;
9,115;  9,097.
9,097. –0,3;
–0,3;  –0,25.
–0,25. , если
, если  1.)
1.)


 ;
; .
. :
:
 , то есть в интервал (6,3848; 11,7248), так как
, то есть в интервал (6,3848; 11,7248), так как  6,75,
6,75,  10,97.
10,97.
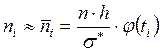 ,
, – опытные частоты,
– опытные частоты,  – теоретические частоты,
– теоретические частоты,  – длина интервала,
– длина интервала,  – объём выборки,
– объём выборки,  – среднее квадратическое отклонение,
– среднее квадратическое отклонение,  – табулированная функция,
– табулированная функция,  .
.
 ; (число одинаковых значений дискретной случайной величины или число наблюдений в i -м интервале в случае непрерывной случайной величины). Такое представление признака и частот называется вариационным рядом.
; (число одинаковых значений дискретной случайной величины или число наблюдений в i -м интервале в случае непрерывной случайной величины). Такое представление признака и частот называется вариационным рядом. где
где  и
и  – соответственно максимальное и минимальное значения признака
– соответственно максимальное и минимальное значения признака  в выборке; l – количество интервалов, причём в данной работе мы будем использовать следующую формулу:
в выборке; l – количество интервалов, причём в данной работе мы будем использовать следующую формулу:  , где n – объём выборки.
, где n – объём выборки. 10,97,
10,97, 
 .
. (10,97–6,75)/10=0,422
(10,97–6,75)/10=0,422  0,43.
0,43. 6,75.
6,75. и длину интервала
и длину интервала 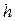 , построим весь интервальный ряд
, построим весь интервальный ряд
 .
. , где
, где 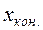 и
и  – конечное и начальное значения определённого интервала. Результаты занесем в таблицу 1.
– конечное и начальное значения определённого интервала. Результаты занесем в таблицу 1.