
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проверка гипотезы о виде распределенияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Проверка гипотезы о законе распределения значения признака Проверяемая (нулевая) гипотеза утверждает, что значения признака в выборке, взятой из генеральной совокупности, распределены по предполагаемому закону. Для проверки гипотезы о виде распределения необходимо вычислить теоретически ожидаемые (выравнивающие) частоты, которые должны были бы получиться, если бы распределение действительно соответствовало предполагаемому. Теоретические частоты 1) в случае дискретной случайной величины 2) в случае непрерывной случайной величины Проверку гипотезы о виде теоретического распределения можно провести с помощью критерия согласия Пирсона
где Гипотеза отвергается, если вычисленное значение Например, если проверяется согласие экспериментальных данных нормальному закону распределения, для которого r =2, то число степеней свободы Следует учитывать, что при использовании критерия согласия Пирсона общее число наблюдений должно быть достаточно большим ( Проверим для нашего примера гипотезу о нормальном законе распределения изучаемой величины для уровня значимости Таблица 4.
Находим с учетом объединения интервалов (объединяем первый, второй и третий интервалы, а также девятый и десятый)
Определим Имеем Вид функции плотности вероятности данной случайной величины, распределённой по нормальному закону в нашем случае:
Интегральная функция распределения такова
Построим кривую Гаусса данного распределения. Найдем максимум кривой Гаусса
   
Рисунок 6. –.Полигон частот и кривая Гаусса
Приложение 1 Таблица значений функции
Приложение 2
Критические точки распределения χ2
ЛИтература
1. Гмурман В.Е. Теория вероятностей и математическая статистика: учеб. пособие для вузов / В.Е. Гмурман. – 12-е изд., перераб. – М.: Высш. образование, 2005. – 479 с. 2. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике: учеб. пособие для вузов / В.Е. Гмурман. - 11-е изд., перераб. - М.: Высш. образование, 2007. - 404 с. 3. Баранова И.М., Часова Н.А. Основы теории вероятностей и математической статистики: учеб. пособие. Ч. 1 Теория вероятностей. / И.М.Баранова [и др.]. – Брянск, 2011. – 140 с. СОДЕРЖАНИЕ
Введение. 4 1. Основные понятия математической статистики. 6 2. Построение вариационного ряда. 7 3. Графическое изображение вариационных рядов. 8 4. Эмпирическая функция распределения. 10 5. Основные выборочные характеристики. 12 6. Точечные и интервальные оценки параметров генеральной совокупности 18 7. Статистическая проверка гипотез. 22 8. Предварительный выбор закона распределения. 25 9. Проверка гипотезы о виде распределения. 28 Приложение 1. 32 Приложение 2. 33 ЛИтература.. 34 Баранова И.М., Часова Н.А.
МАТЕМАТИКА
Статистическая обработка
Методические указания к выполнению расчетно-графической работы для студентов всех направлений подготовки бакалавров
Формат Объем Тираж Заказ
Брянск, Станке Димитрова 3, Редакционно-издательский отдел Отпечатано: Печатный цех БГИТА
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 1128; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.108.87 (0.011 с.) |

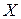 в генеральной совокупности осуществляется с помощью критериев согласия.
в генеральной совокупности осуществляется с помощью критериев согласия. вычисляются по формулам:
вычисляются по формулам: , где
, где  – вероятность случайной величины принять значения равное
– вероятность случайной величины принять значения равное  .
. , где
, где  – середина интервала;
– середина интервала; 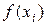 – функция плотности теоретического распределения, вычисленная в точке
– функция плотности теоретического распределения, вычисленная в точке  , основанного на статистике:
, основанного на статистике:
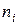 – опытные частоты,
– опытные частоты,  – выравнивающие частоты.
– выравнивающие частоты.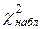 окажется больше критического
окажется больше критического  , найденного по таблицам распределения
, найденного по таблицам распределения  для уровня значимости
для уровня значимости 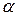 и числа степеней свободы
и числа степеней свободы  , где
, где  – число интервалов,
– число интервалов,  – число оцениваемых параметров предполагаемого теоретического распределения (приложение 2).
– число оцениваемых параметров предполагаемого теоретического распределения (приложение 2). .
. 50), и число наблюдений в интервалах должно быть не менее пяти
50), и число наблюдений в интервалах должно быть не менее пяти  . Интервалы, у которых
. Интервалы, у которых  <5 нужно объединить, а их частоты сложить.
<5 нужно объединить, а их частоты сложить.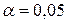 . Найдем выравнивающие частоты.
. Найдем выравнивающие частоты.





 11
11
 11
11
 =
= 
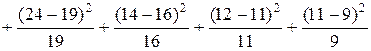 =3,15.
=3,15. =7–3=4, тогда при уровне значимости
=7–3=4, тогда при уровне значимости  имеем
имеем  =9,5.
=9,5. . Следовательно, в рассматриваемом примере нет оснований отвергнуть гипотезу о нормальном распределении изучаемой случайной величины.
. Следовательно, в рассматриваемом примере нет оснований отвергнуть гипотезу о нормальном распределении изучаемой случайной величины. .
. .
. .
.




