
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
симптотический доверительный интервал для параметра l распределения ПуассонаСодержание книги
Поиск на нашем сайте
Пусть . Однако, разрешить неравенство относительно Следовательно Таким образом, искомый асимптотический доверительный интервал уровня
Пусть Рассмотрим статистику , или . Таким образом, искомый асимптотический доверительный интервал уровня
1.Предмет теории вероятностей. Пространство элементарных событий. Понятие случайного события. Определения вероятности. 2.Алгебра случайных событий. 3.Комбинаторика. Элементарная теория вероятностей. Методы вычисления вероятностей. 4. Теоремы сложения и умножения вероятностей. Условная вероятность. 5.Независимые события. 6.Формула полной вероятности. Формула Байеса. 7.Независимые испытания Бернулли. Схема Бернулли 8.Пределные теоремы в схеме Бернулли. Приближенные формулы Лапласа. Теорема Пуассона. 9. Дискретная случайная величина. Типичные законы распределения дискретной величины. 10. Непрерывные случайные величины. Типичные законы распределения. Числовые характеристики непрерывных случайных величин. 11.Случайные векторы. Системы n случайных величин. Равномерное распределение. Условные распределения. 12.Числовые характеристики случайного вектора. Функциональные преобразования случайных векторов.
13.Основные модели законов распределения непрерывных случайных величин 14. Неравенство Маркова. Неравенство Чебышева. Закон больших чисел в форме Чебышева. 15. Центральная предельная теорема. 16 Определение цепи Маркова. Примеры марковских цепей. Многошаговые вероятности перехода. Предельные вероятности 17. Понятие случайной функции (процесса). Классификация. Основные хар-ки случайного процесса 18.Стационарный случайный процесс. Линейные и нелинейные преобразования случайных процессов. Дифференцирование и интегрирование случайных процессов. Спектральное разложение стационарного случайного процесса. 19.Основные статистические описания. Вариационный ряд и эмпирические квантили. Распределение частот. Эмпирический коэффициент корреляция. Межгрупповая дисперсия. 20.Интервальные хар-ки признака. Повторные и бесповторные выборки. Выборочная доля признака. Пропорциональная выборка. 21. Точечные оценки параметров распределения. Методы моментов, максимального правдоподобия, наименьших квадратов. 22. Основные распределения в статистике. Квантилии и процентные точки распределения. Распределения хи-квадрат (закон Пирсона), Стьюента, Фишера, гамма-распределение, бета-распределение. 23. Интервальные статистические оценки. Точные доверительные интервалы. Асимптотические доверительные интервалы. 24. Схема проверки статистической гипотезы. Критерий отношения правдоподобия. Проверка гипотез для одной выборки. Проверка гипотез для двух выборок. 25. Критерий согласия Пирсона. Критерий согласия Колмогорова. Элементы дисперсионного анализа. Статистический анализ экономических временных рядов и прогнозирование. 26.Фукциональная, статистическая и корреляционная зависимости. Коэффициент коррекции. Регрессионные модели как инструмент анализа и прогнозирования экономических явлений. Парная линейная регрессия. 27. Правила принятия решений без использования численного значения вероятностей исходов. Критерий Гурвича.
|
|||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 404; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.26.99 (0.01 с.) |

 выборка, полученная из генеральной совокупности случайной величины
выборка, полученная из генеральной совокупности случайной величины 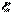 , распределенной по закону Пуассона
, распределенной по закону Пуассона  с неизвестным параметром
с неизвестным параметром  . Требуется построить доверительный интервал для параметра
. Требуется построить доверительный интервал для параметра  .Рассмотрим статистику
.Рассмотрим статистику  . В соответствии с ЦПТ, при
. В соответствии с ЦПТ, при 
 . Пусть
. Пусть 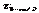 квантиль распределения
квантиль распределения 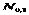 уровня
уровня 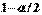 (
( ), тогда:
), тогда: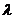 не просто из-за корня в знаменателе. Попробуем заменить в знаменателе
не просто из-за корня в знаменателе. Попробуем заменить в знаменателе  , построив статистику
, построив статистику 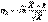 . Не изменится ли при этом характер сходимости? Вспомним свойство сходимости по распределению: если
. Не изменится ли при этом характер сходимости? Вспомним свойство сходимости по распределению: если  а
а 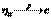 , то
, то  . Тогда:
. Тогда:  , т. к.
, т. к.  .
. ,или
,или  .
. имеет вид:
имеет вид: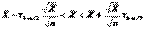 . Асимптотический доверительный интервал для параметра a показательного распределения
. Асимптотический доверительный интервал для параметра a показательного распределения выборка, полученная из генеральной совокупности случайной величины
выборка, полученная из генеральной совокупности случайной величины 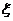 , распределенной по показательному закону
, распределенной по показательному закону  с неизвестным параметром
с неизвестным параметром 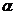 . Требуется построить доверительный интервал для параметра
. Требуется построить доверительный интервал для параметра  . В соответствии с ЦПТ, при
. В соответствии с ЦПТ, при 
 . Пусть
. Пусть  квантиль распределения
квантиль распределения  уровня
уровня  (
(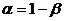 ), тогда:
), тогда: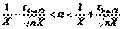 . (3.3)
. (3.3)


