
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Графическое изображение рядов распределения. Наглядно ряды распределения представляются при помощи графических изображений.Содержание книги
Поиск на нашем сайте Ряды распределения изображаются в виде:- Полигона (При построении полигона на горизонтальной оси (ось абсцисс) откладывают значения варьирующего признака, а на вертикальной оси (ось ординат) — частоты или частости.)-Гистограммы(Для построения гистограммы по оси абсцисс указывают значения границ интервалов и на их основании строят прямоугольники, высота которых пропорциональна частотам (или частостям).) -Кумуляты(Распределение признака в вариационном ряду по накопленным частотам (частостям) изображается с помощью кумуляты. Кумулята или кумулятивная кривая в отличие от полигона строится по накопленным частотам или частостям. При этом на оси абсцисс помещают значения признака, а на оси ординат — накопленные частоты или частости)-Огивы(Огива строится аналогично кумуляте с той лишь разницей, что накопленные частоты помещают на оси абсцисс, а значения признака — на оси ординат.) Квантили (процентили) распределения Стьюдента (коэффициенты Стьюдента) — числовые характеристики, широко используемые в задачах математической статистики, таких как построение доверительных интервалов и проверка статистических гипотез.
Часто используемые квантили специальных видов: Проценти́ль Распределение
Распределение хи-квадрат устойчиво относительно суммирования. Если Распределение Стьюдента: Определение. Пусть Плотность распределения Стьюдента:
Свойства распределения Фишера:Если где Гамма распределение и его свойства.Определение. Случайная величина
Действительно, если
|
||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 298; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.006 с.) |

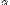 - кванти́ль случайной величины
- кванти́ль случайной величины  с функцией распределения
с функцией распределения  — это любое число
— это любое число  удовлетворяющее двум условиям:1)
удовлетворяющее двум условиям:1)  2)
2)  Заметим, что данные условия эквивалентны следующим:
Заметим, что данные условия эквивалентны следующим: и
и  Если
Если  —непрерывная строго монотонная функция, то существует единственный квантиль
—непрерывная строго монотонная функция, то существует единственный квантиль  любого порядка
любого порядка 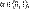 который однозначно определяется из уравнения
который однозначно определяется из уравнения  и, следовательно, выражается через функцию, обратную к функции распределения:
и, следовательно, выражается через функцию, обратную к функции распределения:  Кроме указанной ситуации, когда уравнение
Кроме указанной ситуации, когда уравнение  имеет единственное решение (которое и дает соответствующий квантиль), возможны также две других:если указанное уравнение не имеет решений, то это означает, что существует единственная точка
имеет единственное решение (которое и дает соответствующий квантиль), возможны также две других:если указанное уравнение не имеет решений, то это означает, что существует единственная точка  в которой функция распределения имеет разрыв, которая удовлетворяет данному определению и является квантилем порядка
в которой функция распределения имеет разрыв, которая удовлетворяет данному определению и является квантилем порядка  и
и  (первое неравенство строгое, а второе может быть как строгим, так и обращаться в равенство). если уравнение имеет более одного решения, то все его решения образуют интервал, на котором функция распределения постоянна. В качестве квантиля порядка
(первое неравенство строгое, а второе может быть как строгим, так и обращаться в равенство). если уравнение имеет более одного решения, то все его решения образуют интервал, на котором функция распределения постоянна. В качестве квантиля порядка 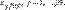 Дециль
Дециль  Квинтиль
Квинтиль  Квартиль
Квартиль  Медиана
Медиана 
 (хи-квадрат) с n степенями свободы — это распределение суммы квадратов n независимыхстандартных нормальныхслучайных величин. Определение Пусть
(хи-квадрат) с n степенями свободы — это распределение суммы квадратов n независимыхстандартных нормальныхслучайных величин. Определение Пусть  — совместно независимые стандартные нормальные случайные величины, то есть:
— совместно независимые стандартные нормальные случайные величины, то есть:  . Тогда случайная величина
. Тогда случайная величина  имеет распределение хи-квадрат с n степенями свободы, обозначаемое
имеет распределение хи-квадрат с n степенями свободы, обозначаемое  .Замечание. Распределение хи-квадрат является частным случаем Гамма распределения:
.Замечание. Распределение хи-квадрат является частным случаем Гамма распределения:  .Следовательно, плотностьраспределения хи-квадрат имеет вид
.Следовательно, плотностьраспределения хи-квадрат имеет вид ,а его функция распределения
,а его функция распределения  ,где
,где  и
и  обозначаютсоответственно полную и неполную гамма-функции. Свойства распределения хи-квадрат
обозначаютсоответственно полную и неполную гамма-функции. Свойства распределения хи-квадрат независимы, и
независимы, и  , а
, а  , то
, то  ; Из определения легко получить моменты распределения хи-квадрат. Если
; Из определения легко получить моменты распределения хи-квадрат. Если  , то
, то  ,
,  ; В силу центральной предельной теоремы, при большом числе степеней свободы распределение случайной величины
; В силу центральной предельной теоремы, при большом числе степеней свободы распределение случайной величины  может быть приближено нормальным
может быть приближено нормальным  . Более точно
. Более точно  по распределению при
по распределению при  .
. - случайная величина распределенная по закону
- случайная величина распределенная по закону  , а
, а  - независимая от нее случайная величина распределенная по закону хи-квадрат с
- независимая от нее случайная величина распределенная по закону хи-квадрат с  степенями свободы. Тогда распределение величины
степенями свободы. Тогда распределение величины 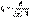 (3.7) называется распределением Стьюдента с
(3.7) называется распределением Стьюдента с  степенями свободы и обозначают
степенями свободы и обозначают  .
. ,
,  (3.8) Числовые характеристики:
(3.8) Числовые характеристики:  ,
,  . Распределение Стьюдента симметрично относительно
. Распределение Стьюдента симметрично относительно  .Так как при
.Так как при  , согласно закону больших чисел,
, согласно закону больших чисел, 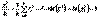 , то при
, то при 
 . Распределе́ние Фи́шера в теории вероятностей — это двухпараметрическое семейство абсолютно непрерывных распределений. Определение: Пусть
. Распределе́ние Фи́шера в теории вероятностей — это двухпараметрическое семейство абсолютно непрерывных распределений. Определение: Пусть 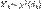 , где
, где 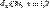 . Тогда распределение случайной величины
. Тогда распределение случайной величины  ,называется распределением Фишера со степенями свободы
,называется распределением Фишера со степенями свободы  и
и  . Пишут
. Пишут  . Моменты: Математическое ожидание и дисперсия случайной величины, имеющей распределение Фишера, имеют вид:
. Моменты: Математическое ожидание и дисперсия случайной величины, имеющей распределение Фишера, имеют вид: , если
, если  ,
, 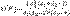 , если
, если  .
. , то
, то  ; Распределение Фишера сходится к единице: если
; Распределение Фишера сходится к единице: если  , то
, то 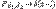 по распределению при
по распределению при  ,
,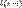 — дельта-функция в единице, то есть распределение случайной величины-константы
— дельта-функция в единице, то есть распределение случайной величины-константы  . Связь с другими распределениями:Если
. Связь с другими распределениями:Если 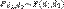 , то случайные величины
, то случайные величины 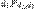 сходятся по распределению к
сходятся по распределению к  при
при  .
. имеет гамма распределение
имеет гамма распределение  , где
, где 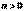 ,
,  , если ее плотность распределения имеет вид:
, если ее плотность распределения имеет вид: (3.4) Здесь
(3.4) Здесь  - гамма функция.
- гамма функция. 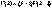 ,
,  ,
,  .Найдем характеристическую функцию случайной величины
.Найдем характеристическую функцию случайной величины 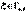 :
: 
 (3.5)Используя, характеристическую функцию легко найти математическое ожидание и дисперсию гамма-распределения:
(3.5)Используя, характеристическую функцию легко найти математическое ожидание и дисперсию гамма-распределения: 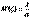 ,
,  . Свойство 1.
. Свойство 1.  есть показательное распределение с параметром
есть показательное распределение с параметром 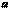 .
. , то
, то  - есть плотность распределения случайной величины, распределенной по показательному закону с параметром
- есть плотность распределения случайной величины, распределенной по показательному закону с параметром  . Свойство 2. Если
. Свойство 2. Если  , то
, то  . Доказательство. Найдем функцию распределения
. Доказательство. Найдем функцию распределения 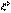 :
:  Свойство 3. Если
Свойство 3. Если  независимы и
независимы и  , то
, то  .
.


