
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Идентификация формы распределения результатов измерений. Критерии согласияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Допустим, что статистический ряд выравнен с помощью некоторой теоретической кривой f(x) (рис.1.1). Обычно в качестве такой кривой принимается функция распределения F(x). Как бы хорошо ни была подобрана теоретическая кривая, между ней и статистическим распределением всегда будут некоторые расхождения. Встает вопрос: чем объясняются эти расхождения? Случайными обстоятельствами, в первую очередь, связанными с малым количеством наблюдений, или неправильно подобранной функцией f(x) º F(x), определяющей эту кривую. Для ответа на этот вопрос служат так называемые критерии согласия. Известен целый ряд таких критериев, предложенных разными авторами. Но идея их применения одинакова и заключается в следующем. Выбирается некоторая величина U, характеризующая степень расхождения между статистическим рядом (распределением), обозначим его F*(x), и теоретическим F(x). Эта величина может быть выбрана различными способами: например, ею может быть простая разница (отклонения) между теоретическим значением функции F(x) и соответствующим этому же значению аргумента х эмпирическим значением F*(x), определенным на основе статистического ряда (гистограммы); максимальная разница F*(x) и F(x); сумма квадратов рассмотренных отклонений; сумма квадратов отклонений, взятых с некоторыми коэффициентами (весами) и др. Очевидно, что величина U, зависящая от СВ F*(x), в свою очередь, также является СВ и закон распределения этой СВ зависит от закона распределения СВ Х, над которой производились измерения (наблюдения), и от числа опытов n. Оказывается, что при некоторых способах выбора меры расхождения U закон ее распределения обладает простыми свойствами и при достаточно большом n практически не зависит от вида функции F(x). Именно такими мерами расхождения и пользуются в математической статистике в качестве критериев согласия.
КРИТЕРИЙ ПИРСОНА Рассмотрим один из наиболее часто применяемых критериев согласия – так называемый критерий c2 (критерий Пирсона). Пусть требуется проверить, согласуются ли экспериментальные данные статистического ряда (табл.1.1.) с гипотезой о том, что СВ Х имеет данный закон распределения, соответствующий выбранной нами теоретической функции распределения F(x) или плотности распределения вероятности f(x). Зная теоретический закон распределения, можно найти теоретические вероятности попадания СВ в каждый из интервалов:
Для проверки согласованности теоретического и статистического распределений, исходим из расхождений между теоретическими вероятностями
Веса интервалов вводятся потому, что отклонения, относящиеся к различным интервалам, нельзя считать равноправными по значимости. Действительно, одно и то же по абсолютной величине отклонение может быть мало значительным, если сама вероятность
то при больших n закон распределения величины U обладает простыми свойствами: он практически не зависит от теоретической функции распределения F(x) и от числа опытов n, а зависит только от числа интервалов При таком способе выбора коэффициентов
где Распределение c2 зависит от параметра
Это условие накладывается всегда, следовательно, во всех случаях, при любых критериях от числа интервалов надо отнимать единицу. Если мы требуем, чтобы совпадали теоретические и статистические средние значения и дисперсии распределений, то необходимо, чтобы выполнялись условия
Для определения числа степеней свободы можно записать следующее выражение Для распределения c2 составлены специальные таблицы (табл.П.1.2). Если бы выбранное теоретическое распределение F(x) для всех Если вычисленная по опытным данным мера расхождения c2 меньше определенного по табл.П.1.2 значения Данные соображения применимы в тех случаях, когда количество опытов n достаточно велико, больше 50, при этом достаточно большим должно быть не только общее число опытов, но и число наблюдений С учетом вышеизложенного схема применения критерия c2 к оценке согласованности теоретического и статистического распределений сводится к следующему: 1. Определяются оценки среднего арифметического значения 2. Группируются результаты измерений (наблюдений) по интервалам длиной h, число которых определяют так же, как и при построении гистограммы. 3. Определяются границы интервалов 4. Для каждого интервала находятся вероятности попадания в него наблюдений. Если в качестве теоретического используется нормальное распределение вероятностей СВ Х, то используются формулы.
где Для распределений, отличающихся от нормального, используются другие формулы. 5. Определяется количество наблюдений 6. Заполняется таблица 1.2 на основе табл.1.1, используемой при построении статистического ряда (п.1.1.1). Таблица 1. 2.
Таблица расчета критерия согласия c2
7. Определяется мера расхождения c2 по ранее приведенной формуле. 8. Определяется число степеней свободы 9. По числу степеней свободы и вероятности из табл.П.1.2 находится критическое значение 10. Сравнивается рассчитанное c2 и критическое значение c2 < c2 >
КРИТЕРИЙ КОЛМОГОРОВА
Кроме критерия Пирсона, для оценки степени согласованности теоретического и эмпирического(статистического) распределений на практике применяется еще и ряд других критериев. Рассмотрим кратко критерий Колмогорова. В качестве меры расхождения между теоретическим и статистическим распределениями А.Н. Колмогоров рассматривает максимальное значение модуля разности между статистической функцией распределения F*(x) и выбранной теоретической функции распределения F(x) (рис.1.3):
Основанием для выбора в качестве меры расхождения величины D является простота ее вычисления и достаточно простой закон распределения. Колмогоров доказал, что какова бы ни была функция распределения F(x) непрерывной СВ Х, при неограниченном возрастании числа независимых наблюдений n вероятность неравенства
стремится к пределу
Значения вероятности
Таблица 1.3 Значения критерия Колмогорова
Схема применения критерия Колмогорова следующая: 1. Строятся статистическая функция распределения F*(x) и предполагаемая теоретическая функция распределения F(x) (рис.1.3). Для их построения составляется таблица с результатами расчетов этих функций по форме табл. 1.4. Функции рассчитываются для нижних границ интервалов, полученных при построении статистического ряда (табл.1.1), используемого затем для построения гистограммы. Оттуда же берутся и вероятности F*(x) равные соответствующим частотам При выборе нормальной функции распределения ее значения определяются с использованием функции Лапласа
Таблица 1.4 Результаты расчета статистической F*(x) и теоретической F(x) функций распределения
2. Определяется максимум D модуля разности между функциями F*(x) и F(x) (рис. 1.3). 3. Определяется величина
4. По табл.1.3 при выбранной вероятности 5. Сравниваются значения
Критерий Колмогорова своей простотой выгодно отличается от описанного ранее критерия c2, поэтому его часто применяют на практике. Однако, этот критерий можно применять только в том случае, когда гипотетическое распределение F(x) полностью известно из каких-либо теоретических соображений. Такой случай на практике встречается довольно редко. Обычно известен только общий вид функции распределения F(x), а входящие в нее числовые параметры (у нормального закона это 2 параметра: математическое ожидание и дисперсия) определяются по исследуемому статистическому материалу. При применении критерия Пирсона это обстоятельство учитывается соответствующим уменьшением числа степеней свободы распределения c2. Критерий же Колмогорова такого не предусматривает. Если все же применять этот критерий в тех случаях, когда параметры теоретического распределения выбираются по статистически данным, критерий дает заведомо завышенные значения вероятности
СОСТАВНОЙ КРИТЕРИЙ Этот критерий применяется для проверки соответствия статистического распределения только нормальному закону и при числе измерений (наблюдений) 15 < n < 50 (допускается от 10), при этом он включает последовательную проверку выполнения двух критериев: критерия 1 и критерия 2. Критерий 1. 1. Вычисляется отношение
2. Проверяется условие
где Если условие выполняется, то гипотеза о том, что исследуемое статистическое распределение соответствует нормальному закону, принимается, в противоположном случае отвергается. Критерий 2. Данный критерий вводится для дополнительной проверки «концов» распределений. Можно считать, что результаты измерений подчиняются нормальному закону, если не более
где
Значение Его проверка ведется в следующем порядке. 1. Задаются уровнем значимости. Он выбирается из таких же соображений, как и при выборе уровня 2. С учетом найденного уровня доверительной вероятности Р вычисляется значение Р/2 и по табл. П.1.3 для него определяется верхняя квантиль 3. Определяется произведение 4. В зависимости от найденного значения Если оно выполняется, то на уровне значимости Гипотеза о нормальности распределения по составному критерию принимается, если выполняются оба критерия. Результирующий уровень значимости составного критерия равен
Величина
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ ОБОРУДОВАНИЕ: 1.Универсальный цифровой измеритель-мультиметр типа М 832, М 838. 2. Набор (не менее 30шт) дискретных элементов – резисторов.
ХОД РАБОТЫ
1. Получить у преподавателя измерительный прибор- мультиметр и внимательно изучить инструкцию по эксплуатации прибора. 2. Получить исследуемые элементы - резисторы, проверить их количество. 3. Установить переключатель пределов измерения прибора в нужное положение и провести измерения сопротивлений всех выданных резисторов, записывая результаты в таблицу по форме табл. 1.5. Таблица 1..5. Результаты измерений сопротивлений резисторов
4. Окончив измерения, сдать мультиметр и резисторы преподавателю.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 841; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.141 (0.01 с.) |

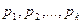 .
. и наблюденными частотами
и наблюденными частотами  . Представляется естественным выбрать в качестве меры расхождения сумму квадратов отклонений (
. Представляется естественным выбрать в качестве меры расхождения сумму квадратов отклонений ( :
: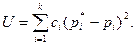
 ,
,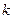 , и при увеличении n приближается к так называемому распределению c2.
, и при увеличении n приближается к так называемому распределению c2.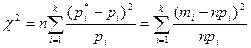 ,
, ,
,  - число значений в
- число значений в  -ом интервале.
-ом интервале. , называемого числом степеней свободы распределения. Оно равно числу интервалов
, называемого числом степеней свободы распределения. Оно равно числу интервалов  = 1.
= 1. ,
,  .
. , где
, где  - количество параметров в теоретическом распределении, на соответствие (согласие) которому проверяется эмпирическое распределение (статистический ряд). Нормальный закон имеет два таких параметра: математическое ожидание и дисперсию, следовательно, у него
- количество параметров в теоретическом распределении, на соответствие (согласие) которому проверяется эмпирическое распределение (статистический ряд). Нормальный закон имеет два таких параметра: математическое ожидание и дисперсию, следовательно, у него 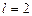 .
. были бы равны нулю, а следовательно, и значение критерия c2 также было бы равно нулю. Таким образом, c2 есть мера суммарного отклонения между теоретическим и экспериментальным распределением.
были бы равны нулю, а следовательно, и значение критерия c2 также было бы равно нулю. Таким образом, c2 есть мера суммарного отклонения между теоретическим и экспериментальным распределением. для заданной вероятности Р, то гипотеза о совпадении экспериментального и выбранного теоретического распределения принимается. Это не значит, что гипотеза верна. Можно лишь утверждать, что она правдоподобна, то есть не противоречит опытным данным. Если же c2 больше значения
для заданной вероятности Р, то гипотеза о совпадении экспериментального и выбранного теоретического распределения принимается. Это не значит, что гипотеза верна. Можно лишь утверждать, что она правдоподобна, то есть не противоречит опытным данным. Если же c2 больше значения  и среднего квадратического отклонения (СКО) s по формулам
и среднего квадратического отклонения (СКО) s по формулам 

 .
. ,
, - функция Лапласа, определяемая по таблице П.1.3, при
- функция Лапласа, определяемая по таблице П.1.3, при  и
и  .
. , попавших в каждый
, попавших в каждый 






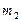









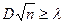


 , подсчитанные по этой формуле, приведены в таблице1.3.
, подсчитанные по этой формуле, приведены в таблице1.3.

 , значения которой табулированы и приведены в табл. П.1.3. Порядок использования этой таблицы аналогичен порядку, применяемому при расчете критерия Пирсона.
, значения которой табулированы и приведены в табл. П.1.3. Порядок использования этой таблицы аналогичен порядку, применяемому при расчете критерия Пирсона.




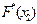






 .
. .
. .
. ,
, и
и  - квантили распределения, определенные по табл.П.4 для количества измерений n и принятого уровня значимости
- квантили распределения, определенные по табл.П.4 для количества измерений n и принятого уровня значимости  = (1, 5 или 10)%. Соответственно Р =
= (1, 5 или 10)%. Соответственно Р = 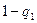 будет равно (99, 95 или 90)%. Проверка условия выполняется для нескольких уровней значимости, чтобы найти тот уровень, при котором условие выполняется.
будет равно (99, 95 или 90)%. Проверка условия выполняется для нескольких уровней значимости, чтобы найти тот уровень, при котором условие выполняется.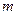 разностей, равных
разностей, равных  превзошли значение
превзошли значение  , то есть выполняется условие
, то есть выполняется условие ,
, -среднее квадратическое отклонение (см. выше критерий Пирсона);
-среднее квадратическое отклонение (см. выше критерий Пирсона); - верхняя квантиль распределения нормированной функции Лапласа для доверительной вероятности Р, которая определяется в зависимости от выбранного уровня значимости
- верхняя квантиль распределения нормированной функции Лапласа для доверительной вероятности Р, которая определяется в зависимости от выбранного уровня значимости  и объема выборки (количества результатов измерений)
и объема выборки (количества результатов измерений)  .
. , по которым необходимо проверять выполнение вышерассмотренного условия.
, по которым необходимо проверять выполнение вышерассмотренного условия. .
. устанавливается в пределах 2¸10%.
устанавливается в пределах 2¸10%.






