
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метрика Джилба оценки сложностиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Одной из наиболее простых, но достаточно эффективных оценок сложности программ является метрика Т. Джилба, в которой логическая сложность программы определяется как насыщенность программы выражениями типа IF – THEN – ELSE. При этом вводятся две характеристики CL – абсолютная сложность программы, характеризующаяся количеством операторов условия; CL = Nу, (2) где Nу- число операторов условия типа IF – THEN – ELSE и cl – относительная сложность программы, характеризующаяся количеством операторов условия, т.е. cl определяется как отношение cl к общему числу операторов.
где N – общее количество операторов
Метрика «граничных значений» оценки сложности
Введем несколько дополнительных понятий, связанных с графом программы. G = (V, E) – ориентированный граф программы с единственной начальной и единственной конечной вершинами. В этом графе число входящих в вершину дуг называется отрицательной степенью вершины, а число исходящих из вершины дуг называется положительной степенью вершины. Тогда набор вершин графа можно разбить на 2 группы: 1. Принимающие вершины – те, у которых положительная степень ≤ 1; 2. Вершины отбора – вершины,, у которой положительная степень ≥ 2. Для получения оценки необходимо разбить исходный граф G на макс. число подграфов G’, удовлетворяющим следующим условиям: - Вход в подграф осуществляется через вершину отбора. - Каждый подграф включает вершину, называемую в дальнейшем «нижняя граница подграфа», в которую можно попасть из любой другой вершины подграфа. Замечание: вершина отбора, соединённая с собой дугой в виде петли, образует подграф (см.рис.3, табл.1). Число вершин, образующих такой подграф, равно скорректированной сложности вершины отбора (табл.2). Каждая принимающая вершина имеет скорректированную сложность равную 1, кроме конечной вершины, скорректированная сложность которой равна 0.
Скорректированные сложности всех вершин графа G суммируются, образуя абсолютную граничную сложность. После этого определяется относительная граничная сложность программы:
Описание алгоритма
1. Находим первую от начала вершину отбора, назовём её А. 2. Идём по одной из ветвей разветвления А до следующей вершины В (не включая её). Это подграф G1’. 3. Проходя далее из вершины отбора В по одной из ветвей до следующей вершины отбора С (не включая её) образуем подграф G2’ и т.д. 4. Из той вершины отбора, из которой организован какой-либо подграф, идём по другой ветви разветвления и организуем очередной подграф Gk. 5. Скорректированная сложность принимающей вершины = 1. 6. Скорректированная сложность вершины отбора равняется числу вершин в подграфе G1’ + число вершин в подграфе G’2 и т.д., столько слагаемых, сколько выходов из этой вершины отбора. 7. Сумма скорректированных сложностей всех скорректированных сложностей графа G даёт абсолютную сложность программы Sa. 8. Расчет относительной сложности. Таблица 1 Подграфы программы
Таблица 2
|
|||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 2036; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.125.137 (0.01 с.) |

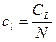 , (3)
, (3)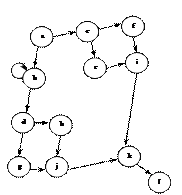
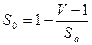 , (4)
, (4) Таким образом, относительная граничная сложность программы равна S0 = 1-(11/25)=0,56.
Таким образом, относительная граничная сложность программы равна S0 = 1-(11/25)=0,56.


