
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уровень автоматизации программированияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Уровень автоматизации программирования можно оценить, основываясь на оценке количества ошибок, сохраняющихся в программе после окончания ее обработки компилятором или другим программным компонентом автоматизации разработки программ.
где В – количество ошибок после реализации программы на языке программирования; Е – интеллектуальные усилия при программировании; V – объем программы; 3000 – критический уровень работы по составлению программы. Появление в языках программирования средств семантического контроля программы (пользовательские типы данных и операторов) потребовало измерения эффективности этих средств. Основным понятием при решении этой задачи является дефект программы. Дефект программы – это такое искажение текста программы, по сравнению с эталонной, которое не обнаруживается при компиляции, но существенно влияет на исход выполнения программы. Следует отметить, что дефект программы может быть и не обнаружен при выполнении программы на определённом множестве исходных данных. Поэтому вводится понятие множества всех потенциальных дефектов D и числа этих дефектов d. Выдвигается гипотеза, согласно которой количество ошибок в программе прямо пропорционально d. Тогда для какого-либо средства статистического семантического контроля можно вычислить показатель его эффективности:
где R1 – количество ошибок в программе, полученное без использования этого средства; R2 – количество ошибок в программе, полученное с использованием данного средства; d1 – количество дефектов в программе, полученное без использования этого средства; d2 – количество дефектов в программе, полученное с использованием данного средства. Теперь необходимо количественно оценить d1 и d2. При оценке количества возможных дефектов, возникающих в тексте программы, оцениваются все случаи замены операторов, операндов и типов, приводящие к изменению смысла алгоритма. Количество дефектов для средств контроля типов данных определится как: dтип = dт + dN1 + dN2 (5) где dт – количество дефектов от возможной замены типов; N1 – количество дефектов от возможной кодов операндов; N2 – количество дефектов от возможной кодов операторов. Таким образом, взяв за основу сравнения полное отсутствие контроля типов данных, эффективность средства контроля типов данных можно оценить по формуле
где Более корректным будет при использовании данной метрики для оценки количества дефектов от возможной замены типов данных dт применять функцию не количества типов, различаемых более развитым средством семантического контроля, а количества разновидностей операндов неконкретного типа. Оно оценивается как разность объема словаря операндов и количества различаемых данным средством программирования типов данных. Тогда оценка эффективности примет вид:
где ТБ – количество типов данных, контролируемых базовым средством программирования; ТК – количество типов данных, контролируемых дополнительным и базовым средством семантического контроля.
Задание Для одной из своих программ рассчитать: 1) Уровень языка, (l); 2) Количество ошибок после реализации программы на языке программирования (В); 3) Количество дефектов для средств контроля типов данных (dтип); 4) эффективность средства контроля типов данных ( КОНТРОЛЬНЫЕ ВОПРОСЫ 1. Что является оценкой языка программирования? 2. Как определить уровень автоматизации программирования? Что является дефектом программы? 3. От чего зависит эффективность контроля типов данных? 4. Как вы понимаете термины семантический контроль и уровень языка? Как на их основе можно оценить уровень языка программирования? ЛИТЕРАТУРА 1. Изосимов А.В., Рыжко А.Л. Метрическая оценка качества программ. – М.: Издательство МАИ, 1989. 2. Холстед М. Начала науки программирования. - М.: Финансы и статистика, 1981.
ПРИЛОЖЕНИЕ 1. СТАТИСТИЧЕСКИЕ ТАБЛИЦЫ Таблица П.1.1 Значения распределения Стьюдента
Таблица П.1.2
Значения c2 в зависимости от r и p
Таблица П.1.3 Значения функции Лапласа
Таблица П.1.4. Квантили распределения величины d
Таблица П.1.5. Значения вероятности Р для вычисления величины
ПРИЛОЖЕНИЕ 2. ОБРАЗЕЦ ВЫПОЛНЕНИЯ И ОФОРМЛЕНИЯ ЛАБОРАТОРНОЙ РАБОТЫ Министерство образования и науки Российской Федерации Федеральное агентство по образованию Марийский государственный технический университет Кафедра ИВС
Лабораторная работа № 2
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 733; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.214.235 (0.011 с.) |

 , (3)
, (3) (4)
(4) (28)
(28) - число типов данных в программе; N1 – общее число операторов в программе; N2 – общее число операндов в программе; η1 – словарь операторов; η2 – словарь операндов.
- число типов данных в программе; N1 – общее число операторов в программе; N2 – общее число операндов в программе; η1 – словарь операторов; η2 – словарь операндов.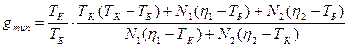 (6)
(6)



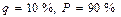
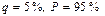




 при
при 



