
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Н. Г. Моисеев, Е. С. СидоркинаСодержание книги
Поиск на нашем сайте
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОСИЙСКОЙ ФЕДЕРАЦИИ МАРИЙСКИЙ ГОСУДАРСТВЕНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Н. Г. МОИСЕЕВ, Е. С. СИДОРКИНА МЕТРОЛОГИЯ, СТАНДАРТИЗАЦИЯ И СЕРТИФИКАЦИЯ Лабораторный практикум
Йошкар-Ола УДК 389(076) Рецензент канд.техн.наук, доцент кафедры ПиП ЭВС МарГТУ В.В.Кошкин; Печатается по решению редакционно-издательского совета МарГТУ
Моисеев Н. Г., Сидоркина Е. С. Метрология, стандартизация, сертификация: Лабораторный практикум / Н.Г. Моисеев, Е.С. Сидоркина – Йошкар-Ола: МарГТУ, 2006. – 94 с.
Даны необходимые теоретические сведения о распределениях случайных составляющих погрешностей измерений, методах обработки результатов измерений и контроля стабильности технологического процесса с помощью контрольных карт, способов оценки качества и надежности программного обеспечения, позволяющих на различных стадиях разработки выявлять просчеты и дефекты программного изделия. Приводится краткое описание последовательности действии при выполнении лабораторных работ и способы обработки полученных результатов. Для студентов направления подготовки 230100 "Информатика и вычислительная техника" и студентов специальности 230101 "Вычислительные машины, комплексы, системы и сети".
УДК 389(076)
Ó Марийский государственный технический университет, 2006 ПРЕДИСЛОВИЕ Данный лабораторный практикум посвящен вопросам метрологии измерений и программного обеспечения. Практикум включает в себя 9 лабораторных работ, каждая из которых начинается с теоретической части, после которой описывается порядок проведения работы и приведена структура отчета по ней. Далее следуют контрольные вопросы и учебно-методическое обеспечение. В первой работе рассматривается вероятностное описание случайных величин (СВ), поскольку в результатах измерения всегда присутствуют случайные составляющие погрешности измерений. Целью работы является приобретение практических навыков построения распределений, применения критериев согласия и оценки выборочных характеристик случайных величин на основе опытных данных, в качестве которых выступают результаты измерений сопротивлений выборки резисторов. Вторая работа во многом базируется на теоретических знаниях и навыках расчетов, полученных в первой работе. Она посвящена обработке результатов прямых многократных измерений, методам исключения грубых погрешностей, получению их точечных и доверительных оценок. В качестве опытных данных используются результаты измерений параметров электронных компонентов: резисторов, конденсаторов, транзисторов, а также отдельных характеристик других объектов. В частности, возможно измерение сопротивления человека – учащегося, проводящего лабораторную работу. Третья и четвертая работа дают новое направление в методах обработки измерений. Оно связано с применением результатов измерений для оценки стабильности технологического процесса производства различных изделий. Даются теоретические сведения о контрольных картах, позволяющих сделать такую оценку и выявить причины, из-за которых нарушена стабильность техпроцесса. В третьей работе на основе опытных данных, полученных по результатам измерений параметров электронных компонентов (резисторов, конденсаторов, транзисторов и др.) даются методы построения различных видов контрольных карт по количественному признаку, а в четвертой, по тем же данным, методы построения контрольных карт по альтернативному признаку. Лабораторные работы с пятой по девятую посвящены метрологии программного обеспечения. Метрология программного обеспечения (ПО) – дисциплина, изучающая проблемы оценивания метрических характеристик качества ПО на этапах от разработки спецификаций до завершения отладки и тестирования программного продукта. В пятой работе изучаются методы оценки метрических характеристик качества программных продуктов По результатам ее выполнения учащиеся приобретают практические навыки по оценке их сложности. В шестой работе изучаются метрики сложности потока управления программ и методы их оценки с точки зрения оценки сложности потока управления, при этом используется теория графов, как методическая основа. Седьмая работа органично, как бы продолжает шестую, и посвящена рассмотрению метрик сложности потока данных и их использованию для оценки сложности программных продуктов. В восьмой работе изучается другой вид метрик – метрики стилистики и понятности программ. Девятая работа завершает цикл работ, посвященных метрологии программного обеспечения, в ней изучаются метрики использования языков программирования и технологических средств. Цель работы состоит в оценке уровня автоматизации программирования, основываясь на оценке количества ошибок, сохраняющихся в программе после окончания ее обработки компилятором или другим программным компонентом автоматизации разработки программ. Лабораторный практикум адресован студентам, обучающимся по направлению подготовки 230100 – "Информатика и вычислительная техника", студентам специальности 230101 – "Вычислительные машины, комплексы, системы и сети", а также студентам специальности 210202 – "Проектирование и технологии электронно-вычислительных средств".
ВВЕДЕНИЕ Измерения с целью определения значений физических величин (массы, длины, скорости и др.) являются главным источником информации во всех сферах деятельности человека. Но из-за несовершенства методов и средств измерений, влияния внешних воздействующих факторов (температуры окружающей среды, ее давления и влажности, вибрации, ускорения, излучений и др.), человеческого фактора истинные значения этих величин получить нельзя. Значения физических величин, полученные измерением, лишь в большей или меньшей степени приближаются к ним. Отклонение результата измерения от истинного значения измеряемой величины называется погрешностью измерения. Так как истинные значения величины установить нельзя, то нужно хотя бы определить границы, в пределах которых оно может находиться с заранее установленной или известной вероятностью. Освоение теоретических положений и выполнение работ, представленных в данном лабораторном практикуме, позволит приобрести навыки по построению распределений случайных величин, определению доверительных или предельных границ истинного значения измеряемой величины, погрешности измерения, оценке стабильности технологического процесса любого изделия. В настоящее время информатизация охватила все сферы человеческой деятельности, компьютеры стали непременным атрибутом многих рабочих мест, и разработка программ приобрела широкий и актуальный характер. При этом программы, как и любой другой продукт, имеют качество, от которого зависит широта их применения. Оценкой качества программ занимается метрология программного обеспечения – дисциплина, изучающая проблемы оценивания метрических характеристик качества ПО на этапах от разработки спецификаций до завершения отладки и тестирования программного продукта. Специалист в любой сфере деятельности должен уметь грамотно определять погрешность результатов различных видов измерений, различных измерительных каналов независимо от того, каким способом представлены пределы допускаемых погрешностей средств измерений, а разработчики программ оценивать их качество, чтобы на различных стадиях разработки выявлять просчеты и дефекты программного изделия.
Требования безопасности перед началом работы
2.1. К лабораторной работе допускаются только лица, прошедшие инструктаж по правилам пользования измерительными приборами, оборудованием и ПЭВМ и изучившими инструкцию на применяемое в проводимой работе оборудование. 2.2. Следует проверить наличие всех составляющих рабочего места: измерительных приборов, оборудования, монитора, клавиатуры, системного блока, «мыши» и коврика для «мыши». 2.3. Следует убедиться в отсутствии видимых повреждений аппаратуры и рабочего места. Визуально проверить исправность штепсельной розетки, целостность проводов питания, штепсельной вилки. О выявленной неисправности сообщить преподавателю. 2.4. Убрать с рабочего места лишние предметы (сумки, папки и прочее). 2.5. Включать компьютеры можно только после разрешения преподавателя.
Требования безопасности во время работы 3.1. Измерительными приборами, оборудованием и компонентами ПЭВМ пользоваться осторожно, не допуская падений и ударов. 3.2. При работе на ПЭВМ сидеть следует прямо, с небольшим наклоном корпуса вперед, не сутулясь. Величина углов в локтевых, тазобедренных и голеностопных суставах должна быть не менее 90 градусов. 3.3. Необходимо соблюдать оптимальное расстояние от глаз до экрана монитора (60-70 см). При меньшем расстоянии глаза быстро устают. 3.4. Клавиатуру следует располагать на поверхности стола на расстоянии 100-300 мм от края стола, обращенного к пользователю. 3.5. При работе на измерительном оборудовании и ПЭВМ и пользовании записями в тетради (книге) последняя должна быть хорошо освещена (не менее 400 люкс) и находиться перед клавиатурой. 3.5. При внезапном отключении электроэнергии в сети выключить все оборудование и ПЭВМ. 3.6. Во время эксплуатации при повреждении штепсельного соединения, токопроводящего кабеля, появления дыма, обнаружении замыкания на корпус немедленно отключить все оборудование и ПЭВМ и доложить о поломке преподавателю. 3.7 Длительность непрерывной работы на компьютерах при сдвоенных уроках по 40 минут в день для студентов I курса; II – III курса до 3 академических часов. После каждого академического часа перерыв 15-20 минут с выходом учащихся из кабинета с обязательным проветриванием. 3.8. Во время регламентированных перерывов с целью снижения нервно-эмоционального напряжения, утомления зрительного анализатора, целесообразно выполнять комплексы упражнений для глаз и физкультминутки (см. приложения). 3.9. Запрещается вскрывать аппаратуру и производить ее ремонт. 3.10. Студенты обязаны бережно относиться к оборудованию, вычислительной технике, раздаточному материалу, мебели. 3.11. Студенты обязаны во время работы соблюдать тишину, не покидать рабочего места без разрешения преподавателя. 3.12. Не использовать программные средства, не относящиеся к теме занятия. 3.13. Не выполнять никаких действий, в благополучном исходе которых нет полной уверенности. 3.14. Не запускать программы, назначение которых неизвестно. 3.15. В случаях затруднений обращаться к преподавателю.
Требования безопасности в аварийной обстановке
4.1. Выключить оборудование и ПЭВМ, при необходимости выключить рубильник. 4.2. Сообщить о случившемся преподавателю. 4.3. Не пользоваться оборудованием и ПЭВМ до полного устранения неисправности. 4.4. При получении травмы и внезапном заболевании немедленно известить руководителя.
Требования безопасности по окончании работы
5.1. Выключить измерительные приборы и оборудование и ПЭВМ. 5.2. Привести в порядок рабочее место, сдать рабочее место преподавателю. 5.2. О всех замечаниях и недостатках в работе измерительных приборов, оборудования и ПЭВМ сообщить преподавателю.
Ответственность 6.1. Ответственность за выполнение инструкции несет зав. кабинетом (лабораторией). Лабораторная работа № 1 ТЕОРЕТИЧЕСКАЯ ЧАСТЬ Присутствие случайных погрешностей в результатах измерения приводит к тому, что результат измерения является случайной величиной (СВ). Поэтому прежде, чем приступить к расчету случайных погрешностей и оценке доверительных интервалов, необходимо ознакомиться с вероятностным описанием СВ.
КРИТЕРИЙ ПИРСОНА Рассмотрим один из наиболее часто применяемых критериев согласия – так называемый критерий c2 (критерий Пирсона). Пусть требуется проверить, согласуются ли экспериментальные данные статистического ряда (табл.1.1.) с гипотезой о том, что СВ Х имеет данный закон распределения, соответствующий выбранной нами теоретической функции распределения F(x) или плотности распределения вероятности f(x). Зная теоретический закон распределения, можно найти теоретические вероятности попадания СВ в каждый из интервалов:
Для проверки согласованности теоретического и статистического распределений, исходим из расхождений между теоретическими вероятностями
Веса интервалов вводятся потому, что отклонения, относящиеся к различным интервалам, нельзя считать равноправными по значимости. Действительно, одно и то же по абсолютной величине отклонение может быть мало значительным, если сама вероятность
то при больших n закон распределения величины U обладает простыми свойствами: он практически не зависит от теоретической функции распределения F(x) и от числа опытов n, а зависит только от числа интервалов При таком способе выбора коэффициентов
где Распределение c2 зависит от параметра
Это условие накладывается всегда, следовательно, во всех случаях, при любых критериях от числа интервалов надо отнимать единицу. Если мы требуем, чтобы совпадали теоретические и статистические средние значения и дисперсии распределений, то необходимо, чтобы выполнялись условия
Для определения числа степеней свободы можно записать следующее выражение Для распределения c2 составлены специальные таблицы (табл.П.1.2). Если бы выбранное теоретическое распределение F(x) для всех Если вычисленная по опытным данным мера расхождения c2 меньше определенного по табл.П.1.2 значения Данные соображения применимы в тех случаях, когда количество опытов n достаточно велико, больше 50, при этом достаточно большим должно быть не только общее число опытов, но и число наблюдений С учетом вышеизложенного схема применения критерия c2 к оценке согласованности теоретического и статистического распределений сводится к следующему: 1. Определяются оценки среднего арифметического значения 2. Группируются результаты измерений (наблюдений) по интервалам длиной h, число которых определяют так же, как и при построении гистограммы. 3. Определяются границы интервалов 4. Для каждого интервала находятся вероятности попадания в него наблюдений. Если в качестве теоретического используется нормальное распределение вероятностей СВ Х, то используются формулы.
где Для распределений, отличающихся от нормального, используются другие формулы. 5. Определяется количество наблюдений 6. Заполняется таблица 1.2 на основе табл.1.1, используемой при построении статистического ряда (п.1.1.1). Таблица 1. 2.
Таблица расчета критерия согласия c2
7. Определяется мера расхождения c2 по ранее приведенной формуле. 8. Определяется число степеней свободы 9. По числу степеней свободы и вероятности из табл.П.1.2 находится критическое значение 10. Сравнивается рассчитанное c2 и критическое значение c2 < c2 >
КРИТЕРИЙ КОЛМОГОРОВА
Кроме критерия Пирсона, для оценки степени согласованности теоретического и эмпирического(статистического) распределений на практике применяется еще и ряд других критериев. Рассмотрим кратко критерий Колмогорова. В качестве меры расхождения между теоретическим и статистическим распределениями А.Н. Колмогоров рассматривает максимальное значение модуля разности между статистической функцией распределения F*(x) и выбранной теоретической функции распределения F(x) (рис.1.3):
Основанием для выбора в качестве меры расхождения величины D является простота ее вычисления и достаточно простой закон распределения. Колмогоров доказал, что какова бы ни была функция распределения F(x) непрерывной СВ Х, при неограниченном возрастании числа независимых наблюдений n вероятность неравенства
стремится к пределу
Значения вероятности
Таблица 1.3 Значения критерия Колмогорова
Схема применения критерия Колмогорова следующая: 1. Строятся статистическая функция распределения F*(x) и предполагаемая теоретическая функция распределения F(x) (рис.1.3). Для их построения составляется таблица с результатами расчетов этих функций по форме табл. 1.4. Функции рассчитываются для нижних границ интервалов, полученных при построении статистического ряда (табл.1.1), используемого затем для построения гистограммы. Оттуда же берутся и вероятности F*(x) равные соответствующим частотам При выборе нормальной функции распределения ее значения определяются с использованием функции Лапласа
Таблица 1.4 Результаты расчета статистической F*(x) и теоретической F(x) функций распределения
2. Определяется максимум D модуля разности между функциями F*(x) и F(x) (рис. 1.3). 3. Определяется величина
4. По табл.1.3 при выбранной вероятности 5. Сравниваются значения
Критерий Колмогорова своей простотой выгодно отличается от описанного ранее критерия c2, поэтому его часто применяют на практике. Однако, этот критерий можно применять только в том случае, когда гипотетическое распределение F(x) полностью известно из каких-либо теоретических соображений. Такой случай на практике встречается довольно редко. Обычно известен только общий вид функции распределения F(x), а входящие в нее числовые параметры (у нормального закона это 2 параметра: математическое ожидание и дисперсия) определяются по исследуемому статистическому материалу. При применении критерия Пирсона это обстоятельство учитывается соответствующим уменьшением числа степеней свободы распределения c2. Критерий же Колмогорова такого не предусматривает. Если все же применять этот критерий в тех случаях, когда параметры теоретического распределения выбираются по статистически данным, критерий дает заведомо завышенные значения вероятности
СОСТАВНОЙ КРИТЕРИЙ Этот критерий применяется для проверки соответствия статистического распределения только нормальному закону и при числе измерений (наблюдений) 15 < n < 50 (допускается от 10), при этом он включает последовательную проверку выполнения двух критериев: критерия 1 и критерия 2. Критерий 1. 1. Вычисляется отношение
2. Проверяется условие
где Если условие выполняется, то гипотеза о том, что исследуемое статистическое распределение соответствует нормальному закону, принимается, в противоположном случае отвергается. Критерий 2. Данный критерий вводится для дополнительной проверки «концов» распределений. Можно считать, что результаты измерений подчиняются нормальному закону, если не более
где
Значение Его проверка ведется в следующем порядке. 1. Задаются уровнем значимости. Он выбирается из таких же соображений, как и при выборе уровня 2. С учетом найденного уровня доверительной вероятности Р вычисляется значение Р/2 и по табл. П.1.3 для него определяется верхняя квантиль 3. Определяется произведение 4. В зависимости от найденного значения Если оно выполняется, то на уровне значимости Гипотеза о нормальности распределения по составному критерию принимается, если выполняются оба критерия. Результирующий уровень значимости составного критерия равен
Величина
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ ОБОРУДОВАНИЕ: 1.Универсальный цифровой измеритель-мультиметр типа М 832, М 838. 2. Набор (не менее 30шт) дискретных элементов – резисторов.
ХОД РАБОТЫ
1. Получить у преподавателя измерительный прибор- мультиметр и внимательно изучить инструкцию по эксплуатации прибора. 2. Получить исследуемые элементы - резисторы, проверить их количество. 3. Установить переключатель пределов измерения прибора в нужное положение и провести измерения сопротивлений всех выданных резисторов, записывая результаты в таблицу по форме табл. 1.5. Таблица 1..5. Результаты измерений сопротивлений резисторов
4. Окончив измерения, сдать мультиметр и резисторы преподавателю.
СОДЕРЖАНИЕ ОТЧЕТА Отчет должен содержать таблицы результатов измерений и расчетов и необходимые графики. Все они должны иметь названия и ссылки с пояснениями в тексте. Отчет имеет следующую структуру: Цель работы. 1. Теоретическая часть. 2. Практическая часть. 2.1. Результаты измерений (должна быть приведена таблица результатов измерений). 2.2. Обработка результатов измерений. 2.2.1. Построение гистограммы. 2.2.2. Расчет и применение критериев согласия (должен содержаться анализ результатов их применения): - критерий Пирсона; - критерий Колмогорова; - составной критерий. Выводы. По результатам работы приводятся общие выводы по работе и записываются аналитически дифференциальная и интегральная функции распределения полученных опытных данных. Пример оформления отчета для всех лабораторных работ приведен в Приложении П.2. КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Дать определение статистической совокупности. 2. Что такое статистический ряд? 3. Что представляет собой гистограмма? 3. Привести порядок построения гистограммы. 4. Какие существуют рекомендации по выбору количества интервалов гистограммы и количества попаданий СВ в интервал. 5. Что представляет собой дифференциальная и интегральная функции распределения, их отличие и графики. 6. Что представляют собой критерии согласия, в чем заключается идея их применения. 7. Какими свойствами обладает распределение c2. Почему оно используется при применении критерия Пирсона? 8. Порядок расчета и применения критерия Пирсона. 9. Порядок расчета и применения критерия Колмогорова. 10. При каких условиях применяется составной критерий. 11. Порядок расчета и применения критерия составного критерия. 12. Сравнить достоинства и недостатки критериев Пирсона, Колмогорова и составного критерия.
УЧЕБНО-МЕТОДИЧЕСКОЕ ОБЕСПЕЧЕНИЕ 1. Вентцель Е.С. Теория вероятностей. М.: Наука, 1969. 2. Смирнов Н.В., Дудин-Барковский И.В. Курс теории вероятностей и математической статистики для технических приложений. М.: Наука, 1965. 3.Новицкий П.В., Зограф И.А. Оценка погрешностей результатов измерений. М.: Энергоатомиздат, 1985.
Лабораторная работа № 2 ТЕОРЕТИЧЕСКАЯ ЧАСТЬ Прямые многократные измерения делятся на равно- и неравноточные. В данной лабораторной работе будет рассмотрен порядок обработки прямых многократных равноточных измерений. Равноточными называются измерения, которые проводятся средствами измерений одинаковой точности по одной и той же методике при неизменных внешних условиях. При равноточных измерениях СКО результатов всех выборок измерений равны между собой. З
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 391; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.168.68 (0.017 с.) |

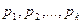 .
. и наблюденными частотами
и наблюденными частотами  . Представляется естественным выбрать в качестве меры расхождения сумму квадратов отклонений (
. Представляется естественным выбрать в качестве меры расхождения сумму квадратов отклонений ( :
: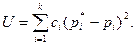
 ,
,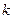 , и при увеличении n приближается к так называемому распределению c2.
, и при увеличении n приближается к так называемому распределению c2.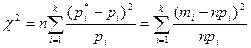 ,
, ,
,  - число значений в
- число значений в  -ом интервале.
-ом интервале. , называемого числом степеней свободы распределения. Оно равно числу интервалов
, называемого числом степеней свободы распределения. Оно равно числу интервалов  = 1.
= 1. ,
,  .
. , где
, где  - количество параметров в теоретическом распределении, на соответствие (согласие) которому проверяется эмпирическое распределение (статистический ряд). Нормальный закон имеет два таких параметра: математическое ожидание и дисперсию, следовательно, у него
- количество параметров в теоретическом распределении, на соответствие (согласие) которому проверяется эмпирическое распределение (статистический ряд). Нормальный закон имеет два таких параметра: математическое ожидание и дисперсию, следовательно, у него 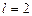 .
. были бы равны нулю, а следовательно, и значение критерия c2 также было бы равно нулю. Таким образом, c2 есть мера суммарного отклонения между теоретическим и экспериментальным распределением.
были бы равны нулю, а следовательно, и значение критерия c2 также было бы равно нулю. Таким образом, c2 есть мера суммарного отклонения между теоретическим и экспериментальным распределением. для заданной вероятности Р, то гипотеза о совпадении экспериментального и выбранного теоретического распределения принимается. Это не значит, что гипотеза верна. Можно лишь утверждать, что она правдоподобна, то есть не противоречит опытным данным. Если же c2 больше значения
для заданной вероятности Р, то гипотеза о совпадении экспериментального и выбранного теоретического распределения принимается. Это не значит, что гипотеза верна. Можно лишь утверждать, что она правдоподобна, то есть не противоречит опытным данным. Если же c2 больше значения  и среднего квадратического отклонения (СКО) s по формулам
и среднего квадратического отклонения (СКО) s по формулам 

 .
. ,
, - функция Лапласа, определяемая по таблице П.1.3, при
- функция Лапласа, определяемая по таблице П.1.3, при  и
и  .
. , попавших в каждый
, попавших в каждый 






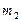









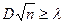


 , подсчитанные по этой формуле, приведены в таблице1.3.
, подсчитанные по этой формуле, приведены в таблице1.3.

 , значения которой табулированы и приведены в табл. П.1.3. Порядок использования этой таблицы аналогичен порядку, применяемому при расчете критерия Пирсона.
, значения которой табулированы и приведены в табл. П.1.3. Порядок использования этой таблицы аналогичен порядку, применяемому при расчете критерия Пирсона.




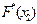






 .
. .
. .
. ,
, и
и  - квантили распределения, определенные по табл.П.4 для количества измерений n и принятого уровня значимости
- квантили распределения, определенные по табл.П.4 для количества измерений n и принятого уровня значимости  = (1, 5 или 10)%. Соответственно Р =
= (1, 5 или 10)%. Соответственно Р = 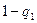 будет равно (99, 95 или 90)%. Проверка условия выполняется для нескольких уровней значимости, чтобы найти тот уровень, при котором условие выполняется.
будет равно (99, 95 или 90)%. Проверка условия выполняется для нескольких уровней значимости, чтобы найти тот уровень, при котором условие выполняется.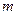 разностей, равных
разностей, равных  превзошли значение
превзошли значение  , то есть выполняется условие
, то есть выполняется условие ,
, -среднее квадратическое отклонение (см. выше критерий Пирсона);
-среднее квадратическое отклонение (см. выше критерий Пирсона); - верхняя квантиль распределения нормированной функции Лапласа для доверительной вероятности Р, которая определяется в зависимости от выбранного уровня значимости
- верхняя квантиль распределения нормированной функции Лапласа для доверительной вероятности Р, которая определяется в зависимости от выбранного уровня значимости  и объема выборки (количества результатов измерений)
и объема выборки (количества результатов измерений)  .
. , по которым необходимо проверять выполнение вышерассмотренного условия.
, по которым необходимо проверять выполнение вышерассмотренного условия. .
. устанавливается в пределах 2¸10%.
устанавливается в пределах 2¸10%.






