
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метрики сложности потока данныхСодержание книги
Поиск на нашем сайте
ЦЕЛЬ РАБОТЫ: оценить сложность программных продуктов, используя метрики сложности потока данных.
Следующая группа метрик сложности программ - метрики сложности потока данных, т.е. использования, конфигурации и размещения данных в программах.
1. Метрика "модуль – глобальная переменная" Метрика "модуль – глобальная переменная". Обозначается как (p, r), где p - модуль, имеющий доступ к глобальной переменной r. В зависимости от наличия в программе реального обращения к переменной r формируются два типа пар "модуль – глобальная переменная": фактические и возможные. Возможное обращение к r с помощью p показывает, что область существования r включает в себя p. Характеристика Aup – количество переменных, показывает, сколько раз модули Up действительно получали доступ к глобальным переменным, а число PUp сколько раз они могли бы получить доступ, т.е. Pup – количество глобальных переменных, к которым мог бы получить доступ модуль. Отношение числа фактических обращений к возможным определяется
Эта формула показывает приближенную вероятность ссылки произвольного модуля на произвольную глобальную переменную. Очевидно, чем выше эта вероятность, тем выше вероятность "несанкционированного" изменения какой-либо характеристики, что может существенно осложнить работы, связанные с модификацией программы. Пример: пусть в программе имеются 3 глобальные переменные (x, y, z) и 3 подпрограммы. Если предположить, что каждая подпрограмма имеет доступ к каждой из переменных, то получим девять возможных пар Pup = 3перем · 3подпрог = 9. Далее пусть первая подпрограмма обращается к одной переменной (x), вторая – к двум (y, z), а третья – не обращается ни к одной переменной, тогда. Aup = 1 + 2 + 0 = 3, следовательно,
2. "спен" Следующей метрикой сложности потока данных является "спен". Определение спена основывается на локализации обращений к данным внутри каждой программной секции. «Спен» - это число утверждений, содержащих данный идентификатор между его первым и последним появлением в тексте. Идентификатор, появившийся n раз, имеет спен равный n-1. Усреднённый по всем идентификаторам, «Спен» даёт сложность программы. Пример: Пусть у нас имеется 7 идентификаторов. 2 - «Спен» 12, 2 - «Спен» 41 и 3 - «Спен» 80.
Следовательно, при построении трассы программы необходимо будет ввести в тело программы, по крайней мере, 50 контролирующих утверждений, что усложнит тестирование и отладку.
Метрика Чепина.
Другой метрикой сложности потока данных является метрика Чепина. Суть метода состоит в оценке информационной прочности отдельно взятого программного модуля с помощью анализа характера использования переменных из списка ввода-вывода. Все множество переменных, составляющих список ввода-вывода разбивается на 4 группы: 1. множество Р – это переменные вводимые для расчётов и обеспечения вывода. (Примером может служить используемая в программах лексического анализатора переменная, содержащая строку исходного текста программы, т.е. сама переменная не модифицируется, а только содержит исходную информацию). 2. множество М – модифицируемые или создаваемые внутри программы переменные. 3. множество С – переменные, участвующие в управлении работой программного модуля (управляющие переменные). 4. множество Т – переменные, не используемые в данной программе (паразитные переменные). Поскольку каждая переменная может выполнять одновременно несколько функций, необходимо учитывать ее в каждой соответствующей функциональной группе. Далее вводится значение метрики Чепина: Q = а1 P + а2 М + а3 С + а4 Т, (3) где α1, α2, α3, α4 – весовые коэффициенты, используемые для отражения различного влияния на сложность программы каждой функциональной группы. По мнению автора метрики: α1 = 1, α2 = 2, α3 = 3, α4 = 0,5. Таким образом наибольший вес, равный трем, имеет функциональная группа С, т.к. она влияет на поток управления. Весовой коэффициент группы Т не равен нулю, поскольку "паразитные" переменные не увеличивают сложность программы, но затрудняют ее понимание. С учетом весовых коэффициентов выражение (3) примет вид Q = P + 2М + 3С + 0,5Т (4) Следует отметить, что рассмотренные метрики сложности программ основаны на анализе исходных текстов программ и графов, что обеспечивает единый подход к автоматизации их расчета
ЗАДАНИЕ
Для одной из своих программ рассчитать: 1) Отношение числа фактических переменных к возможным RUp; 2) Метрики Чепина, (T,P,С, M, Q); 3) Спен (Scp).
КОНТРОЛЬНЫЕ ВОПРОСЫ 1. Что называется метриками сложности? Что такое "Спен"? 2. Что показывает метрика "Модуль – глобальная переменная", опишите принцип нахождения этой метрики. 3. Как построить поцесс тестирования и отладки на основе метода "Спена"? 4. Как оценить информационную прочность отдельного программного модуля? Метрика Чепина. ЛИТЕРАТУРА 1. Изосимов А.В., Рыжко А.Л. Метрическая оценка качества программ. – М.: Издательство МАИ, 1989.
Лабораторная работа № 8
|
||
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 970; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |

 . (1)
. (1)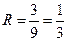 .
. (2)
(2)


