
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Критерии исключения грубых погрешностейСодержание книги
Поиск на нашем сайте При однократных измерениях промах обнаружить невозможно. Для уменьшения вероятности появления промахов измерения проводят два-три раза и за результат принимают среднее арифметическое значение полученных отсчетов. При многократных измерениях для обнаружения промахов используют статистические критерии, предварительно определив, какому виду распределения соответствует результат измерений. Для выявления грубых погрешностей задаются вероятностью q (уровнем значимости) того, что сомнительный результат действительно мог присутствовать в данной совокупности результатов измерений. Критерий «трех сигм» применяется для результатов измерений, распределенных по нормальному закону. По этому критерию считается, что результат, возникающий с вероятностью q ≤ 0,003 маловероятен, и его можно считать промахом, если граница цензурирования Это правило обычно считается слишком жестким, поэтому рекомендуется назначать границу цензурирования в зависимости от объема выборки: при 6 < n ≤ 100 при 100 < n ≤ 1000 при 1000 < n ≤ 10000
Критерий Романовского применяется, если число измерений n < 20. При этом вычисляется отношение
Таблица 2.2 Значения критерия Романовского β = f(n)
Если β ≥ Пример 1. При диагностировании топливной системы результаты пяти измерений расхода топлива составили: 22, 24, 26, 28, 30 л на 100 км. Последний результат вызывает сомнение. Проверить по критерию Романовского, не является ли он промахом. Решение. Находим среднее арифметическое значение расхода топлива и его СКО без учета последнего результата, то есть для четырех измерений. Они соответственно равны 25 и 2,6 л на 100км. Поскольку n < 20, то применяется критерий Романовского. При уровне значимости 0,01 и n = 4 табличный коэффициент Критерий Романовского свидетельствует о необходимости отбрасывания последнего результата измерения. Критерий Шарлье используется, если число наблюдений в ряду велико (n > 20). Тогда (по теореме Бернулли) число результатов, превышающих по абсолютному значению среднее арифметическое значение на величину
где Пользуясь критерием Шарлье, отбрасывают результат, для которого в ряду из n наблюдений выполняется неравенство
Таблица 2..3 Значения критерия Шарлье
Вариационный критерий Диксона Кд удобный и достаточно мощный (с малыми вероятностями ошибок). Применяется при числе наблюдений n < 30. При его применении полученные результаты наблюдений записывают в вариационный возрастающий ряд Пример 2. Было проведено пять измерений напряжения в электросети. Получены следующие результаты: 127,1; 127,2; 126,9; 127,6; 127,2. Результат 127,6В существенно (на первый взгляд) отличается от остальных. Проверить, не является ли он промахом. Решение. Составим вариационный ряд из результатов измерений напряжения в электросети: 126,9; 127,1; 127,2; 127,2; 127,6. Для крайнего члена этого ряда 127,6 критерий Диксона
Кд = (127,6 – 127,2) / (127,6 – 126,9) = 0,4 / 0,7 = 0,57
Таблица 2.4 Значения критерия Диксона
Как следует из табл.2.4 по этому критерию результат 127,6В может быть отброшен как промах лишь на уровне значимости q = 0,10. Применение рассмотренных критериев требует осмотрительности и учета объективных условий измерения. Оператор должен исключить результат наблюдения с явной грубой погрешностью и выполнить новое измерение. Но нельзя просто отбрасывать более или менее резко отличающиеся от других результаты наблюдений. В сомнительных случаях лучше сделать дополнительные измерения (не взамен сомнительных, а кроме них) и затем использовать рассмотренные критерии.
СУММИРОВАНИЕ ПОГРЕШНОСТЕЙ
Суммирование систематических погрешностей. Неисключенная систематическая погрешность результата измерения включает составляющие, обусловленные методом, средствами измерений и другими источниками. Если случайные погрешности малы, то в качестве границ неисключенной систематической погрешности принимают пределы допускаемых основных и дополнительных погрешностей СИ. При суммировании неисключенных систематических погрешностей их рассматривают как случайные величины с равномерным законом распределения. 1. Границы неисключенных систематических погрешностей результата измерения определяются по формуле
где
2. При Р < 0,99 коэффициент k мало зависит от Таблица 2.5 Значения коэффициента k для различных значений Р и m
3. При Р ³ 0,99 коэффициент k значительно зависит от числа слагаемых m и соотношения между ними. Поэтому при m > 4 рекомендуется принимать среднее значение k = 1,4, а при m £ 4 значение k необходимо уточнить по ГОСТ 8.207-76 или табл.2.6.
Таблица 2. 6
Значения коэффициента k для различных значений m, C при Р = 0,99
Параметр С, равный отношению границ составляющих систематической погрешности 4. При большом числе слагаемых результирующая погрешность имеет практически нормальное распределение. Оценка дисперсии этого распределения равна сумме дисперсий слагаемых
Задавшись доверительной вероятностью, получим Q как границу доверительного интервала
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 764; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |

 , где
, где  – оценка СКО измерений, а все
– оценка СКО измерений, а все  признаются промахами и исключаются из дальнейших расчетов. Величины
признаются промахами и исключаются из дальнейших расчетов. Величины  и
и  . Данный критерий надежен при числе измерений n ≥20…50.
. Данный критерий надежен при числе измерений n ≥20…50. ,
, ,
, .
. и сравнивается с критерием
и сравнивается с критерием 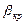 , выбранным по табл.2.2.
, выбранным по табл.2.2.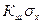 , будет
, будет ,
, - значениенормированнойфункции Лапласа для
- значениенормированнойфункции Лапласа для  . Если сомнительным в ряду результатов наблюдений является один результат, то
. Если сомнительным в ряду результатов наблюдений является один результат, то  . Значения критерия Шарлье приведены в табл. 2.3.
. Значения критерия Шарлье приведены в табл. 2.3.

 . Критерий Диксона определяется как
. Критерий Диксона определяется как  Критическая область для этого критерия
Критическая область для этого критерия  . Значения
. Значения  zq приведены в табл.2.4.
zq приведены в табл.2.4. ,
, - граница i – й неисключенной систематической погрешности;
- граница i – й неисключенной систематической погрешности;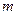 - число неисключенных систематических погрешностей;
- число неисключенных систематических погрешностей;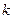 - коэффициент, зависящий от числа слагаемых
- коэффициент, зависящий от числа слагаемых  , принимается равным наименьшему значению указанного отношения при условии, что
, принимается равным наименьшему значению указанного отношения при условии, что  .
. .
. , где
, где  - квантиль нормального распределения при выбранном уровне значимости q = 1 – P.
- квантиль нормального распределения при выбранном уровне значимости q = 1 – P.


