
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема об отсутствии верхней границы сложности вычисленийСодержание книги
Поиск на нашем сайте Теорема 1: О не существовании верхней границы сложности вычисления. Для любой общерекурсивной функции Т.е. ограничения на сложность вычисления не существует. Не существует общерекурсивной функции которая ограничила бы сверху сложность вычисления любой функции. Всегда найдётся такая функция сложность вычисления которой больше чем любое предположенное значение.
Теорема 2: О существовании сложновычислимой функции. Для любой общерекурсивной функции 1) Для всех x кроме конечного числа точек 2) Сложность вычисления которой будет
Теорема Блюма о линейном ускорении Теорема 3: Теорема Блюма. Для любой общерекурсивной функции Рассмотрим следствия этой теоремы: 1. Пусть существует функция Т.е. существует босконечная последовательность машин Таким образом не существует нижней границы сложности вычисления. Существуют задачи которые всегда можно ускорить. 2. Пусть существует функция Возьмём более быстрый процессор, который будет совершать 2 шага за 1 нс, тогда общее время выполнения программы на новом процессоре будет Используем новый алгоритм решения Таким образом общее время на выполнение программы на старом процессоре но с новым алгоритмом меньше затраченного времени на выполнение такой же задачи на новом процессоре, но по старому алгоритму. Из этого следует вывод, что поиск новых алгоритмов эффективнее, чем построение более быстродейственной техники. Необходимо искать новые алгоритмы решения задач.
Сложность массовой проблемы Каждая массовая проблема может быть решена на определенной машине Тьюринга. Пусть имеется массовая задача
Если индивидуальная задача имеет решение, МТ будет иметь вид:
Схема кодировки - способ погружение массовой проблемы в алфавит. Сложность задачи можно охарактеризовать функциями сложности: 1. 2. Возможно ли оценить нижнюю границу сложности? Существуют методы прямого получения нижних оценок. Пример: метод следов. Методом следов можно определить сложность следующих задач: 1. Является ли произвольное слово p - симметричным. 2. Является ли P декартовым квадратом Установление прямых нижних оценок сложности задач затруднительно. В связи с этим получил подход, связанный с получением косвенных нижних оценок, т.е. установление таких утверждений, в которых существование эффективного разрешающего алгоритма для конкретной задачи влечет за собой существование эффективного алгоритма для многих общепризнанно трудных задач. Выделяют следующие классы сложности 1. Класс p – полиноминальная сложность. Говорят, что машина Т решает задачу 2. Класс Е. В противном случае говорят, что машина Т решает задачу a. Если сложность задачи апроксимируется функцией, которая возрастает быстрее любого полинома, но медленнее любой показательной функции b. Если сложность задачи апроксимируется функцией, которая возрастает быстрее любой показательной функции Практическая значимость класса P Какую задачу можно решить при заданной скорости быстродействия
Для того, чтобы решать задачи больших размерностей мы либо увеличиваем время, либо увеличиваем производительность. Из таблицы видно, что полиноминальные алгоритмы лучше реагируют на увеличение размерности задач, а любой экспоненциальный алгоритм, начиная с некоторой размерности, оказывается практически не решаемым. Это означает, что при Вывод: полиноминальная задача - легко решаемая, экспоненциальная задача – трудно решаемая. Свойства класса P полиноминальных задач: 1. Класс P одинаков для всех разумных алгоритмических моделей (ЧРФ, машины поста и т. д.) 2. Схема кодирования является существенной при выделении класса P. При изменении схем кодировки задача может стать экспоненциальной. Поэтому нужно обязательно указывать схему кодировки. 3. Класс P является замкнутым – можно комбинировать полиноминальные алгоритмы, используя один в качестве «подпрограммы» другого и при этом результирующий алгоритм будет полиноминальным. Примеры лёгкорешаемых и труднорешаемых задач Пусть имеется множество 1. Поиск наибольшего элемента 2. Упорядочивание элементов в порядке возрастания 3. Установление является ли отношение 4. Проверка является ли отношение 5. Задача выполнимости КНФ. Пусть имеется формула Определим теперь класс Для каждой задачи распознавания Примеры задач удостоверения: 1. Имеет ли уравнение 2. Пусть дана задача проверки гамильтоновости бинарного отношения. Если R – гамильтоново отношение, то удостоверением этого будет последовательность элементов 3. Пусть дана задача проверки выполнимости КНФ. Если Хотя задачи 2 и 3 решается за экспоненциальное время, соответствующие им задачи удостоверения решается за полиноминальное время.
Класс «NP»
Класс

Угадывающий модуль (Оракул) начинает работать в момент времени
Сложность НТ: Сложность вводится только в том случае, когда соответствующая задача распознавания имеет ответ «Да», иначе сложность не определена. Чтобы задача принадлежала классу
Свойства класса NP: 1.

Для одного слова К просматриваем один такт работы. Для 2 –х слов KKпросматриваем два такта работы. Если слово занимает одну ячейку смотрим остановится ли машина Тьюринга за один такт Если слово занимает две ячейки смотрим остановится ли машина Тьюринга за 2 такта. 2. Класс 3. Класс
Как соотносятся классы
Существует много фактов, что
|
|||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 525; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.141 (0.007 с.) |

 (с помощью которой пытаемся ограничить сложность) существует общерекурсивная 0,1-функция
(с помощью которой пытаемся ограничить сложность) существует общерекурсивная 0,1-функция  такая что существует значение
такая что существует значение  для которого справедливо
для которого справедливо 
 при всех
при всех  т.е.:
т.е.: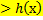 почти во всех точках x т.е. почти для всех x.
почти во всех точках x т.е. почти для всех x. существует общерекурсивная функция с коротким ответом (0, 1)
существует общерекурсивная функция с коротким ответом (0, 1)  вычисляющей f(x) найдется машина
вычисляющей f(x) найдется машина  вычисляющая f(x) такая что
вычисляющая f(x) такая что 
 и тогда существует
и тогда существует 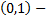 функция f(x) которая допускает вычисление со сложность
функция f(x) которая допускает вычисление со сложность  причём
причём  в свою очередь для
в свою очередь для  справедливо выражение
справедливо выражение 



 и запустим его на первом процессоре, тогда общее время выполнения программы будет
и запустим его на первом процессоре, тогда общее время выполнения программы будет  , т.е.
, т.е. 
 , характеризуемая множеством параметров,
, характеризуемая множеством параметров,  - индивидуальная задача, в которой эти параметры фиксированы. Пусть с массовой задачей
- индивидуальная задача, в которой эти параметры фиксированы. Пусть с массовой задачей  , которая ставит каждой индивидуальной задаче в соответствие слово
, которая ставит каждой индивидуальной задаче в соответствие слово  в некотором алфавите
в некотором алфавите  . При этом размером задачи
. При этом размером задачи  понимается длинна машинного слова
понимается длинна машинного слова 
 - погружение индивидуальной массовой проблемы во внешний алфавит.
- погружение индивидуальной массовой проблемы во внешний алфавит.
 , где
, где  - временная сложность по худшему случаю,
- временная сложность по худшему случаю,  -длина машинного слова.
-длина машинного слова. , где
, где 

 за полиноминальное время, если существует многочлен, который аппроксимирует сложность массовой проблемы
за полиноминальное время, если существует многочлен, который аппроксимирует сложность массовой проблемы 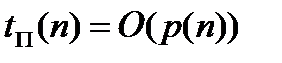 . Если задача решается за полиноминальное время, то она принадлежит классу р.
. Если задача решается за полиноминальное время, то она принадлежит классу р. за экспоненциальное время
за экспоненциальное время  - экспоненциальная сложность задачи.
- экспоненциальная сложность задачи. , то задача имеет субэкспоненциальную сложность.
, то задача имеет субэкспоненциальную сложность. , то задача имеет гиперэкспоненциальную сложность.
, то задача имеет гиперэкспоненциальную сложность.



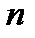









 не решаем сейчас, а также не решаем в обозримом будущем. Если полиноминальный алгоритм не решаем сейчас, то его можно будет решить в обозримом будущем.
не решаем сейчас, а также не решаем в обозримом будущем. Если полиноминальный алгоритм не решаем сейчас, то его можно будет решить в обозримом будущем. .
.

 . Имеется алгоритм порядка
. Имеется алгоритм порядка  - каждый элемент нужно сравнить с каждым.
- каждый элемент нужно сравнить с каждым. 
 на множестве
на множестве  отношением эквивалентности. Задачу зададим матрицей
отношением эквивалентности. Задачу зададим матрицей  ,где
,где  Для того, чтобы отношение M являлось отношением эквивалентности необходимо выполнение условий:
Для того, чтобы отношение M являлось отношением эквивалентности необходимо выполнение условий:  Для решения задачи необходимо проверить
Для решения задачи необходимо проверить  условий. Сложность задачи
условий. Сложность задачи 
 на множестве
на множестве  гамильтоновым. Бинарное отношение является гамильтоновым, если элементы
гамильтоновым. Бинарное отношение является гамильтоновым, если элементы  можно так упорядочить
можно так упорядочить  , что выполнено соотношение
, что выполнено соотношение  . В настоящее время неизвестно полиноминального алгоритма
. В настоящее время неизвестно полиноминального алгоритма  проверки гамильтоновости произвольного отношения
проверки гамильтоновости произвольного отношения  упорядочивований
упорядочивований 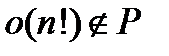 .
. от булевых переменных
от булевых переменных  в некотором фиксированном базисе
в некотором фиксированном базисе  . Пусть формула
. Пусть формула  где
где  , если переменна присутствует в КНФ в составе элементарной дизъюнкции и
, если переменна присутствует в КНФ в составе элементарной дизъюнкции и  , если переменной нет. Входными данными в эту задачу является
, если переменной нет. Входными данными в эту задачу является 
 . Задача состоит в чтобы определить существует ли такой набор значений для
. Задача состоит в чтобы определить существует ли такой набор значений для  . На настоящий момент не известно полиноминального алгоритма решения этой задачи. Тривиальный алгоритм предполагает проверку всех возможных значений
. На настоящий момент не известно полиноминального алгоритма решения этой задачи. Тривиальный алгоритм предполагает проверку всех возможных значений  , т. е. требует перебора
, т. е. требует перебора  наборов значений переменных
наборов значений переменных  .
. 
 задач распознавания, т. е. имеющих ответ «ДА» или «НЕТ».
задач распознавания, т. е. имеющих ответ «ДА» или «НЕТ».  . Для того, чтобы задача
. Для того, чтобы задача  содержалась в классе
содержалась в классе  имеет ответ «Да», то существует слово
имеет ответ «Да», то существует слово  , длины, ограниченной полиномом от размера
, длины, ограниченной полиномом от размера  такое, что задача с начальными данными
такое, что задача с начальными данными  принадлежит
принадлежит  . Слово
. Слово  .
. можно определить соответствующую задачу удостоверения
можно определить соответствующую задачу удостоверения  .
. для набора коэффициентов
для набора коэффициентов  решение в целых числах.
решение в целых числах.  Доказательство существования решение – предъявление этого решения:
Доказательство существования решение – предъявление этого решения: 
 - конкретный набор номеров элементов для которого выполняется свойство гамильтоновсти.
- конкретный набор номеров элементов для которого выполняется свойство гамильтоновсти. .
. определяется через понятие недетерменированного алгоритма. Введем понятие недетерминированной машины Тьюринга (машина с оракулом).
определяется через понятие недетерменированного алгоритма. Введем понятие недетерминированной машины Тьюринга (машина с оракулом). 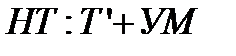






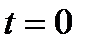 , двигается влево от МТ и пишет слово догадку (по одному символу за такт) через разделитель. Дальше
, двигается влево от МТ и пишет слово догадку (по одному символу за такт) через разделитель. Дальше  работает как обычная
работает как обычная  .
. 
 существует слово-догадка такое, что
существует слово-догадка такое, что  , где
, где  - сложность работы УМ (длина слова -догадки),
- сложность работы УМ (длина слова -догадки), 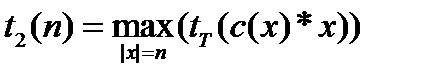 - сложность решения детерминированного алгоритма.
- сложность решения детерминированного алгоритма.
 существует алгоритм, который позволяет решить эту задачу со сложностью
существует алгоритм, который позволяет решить эту задачу со сложностью  , где p – некоторый полином. Существует НТ,
, где p – некоторый полином. Существует НТ, 
 . Всего может быть записано
. Всего может быть записано  , где k – мощность внешнего алфавита задачи,
, где k – мощность внешнего алфавита задачи,  . Для каждой из догадок существует такой
. Для каждой из догадок существует такой  , что через
, что через  шагов НТ остановится в позиции
шагов НТ остановится в позиции  , либо вообще не остановится
, либо вообще не остановится 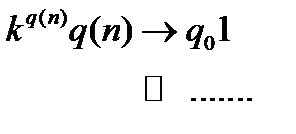 проделав
проделав  шагов если мы пришли в положение
шагов если мы пришли в положение  - ответ «Да», иначе переходим к новому слову. Если она не остановилась ни для одного слова, то ответ будет «Нет».
- ответ «Да», иначе переходим к новому слову. Если она не остановилась ни для одного слова, то ответ будет «Нет».  . Мы должны перебрать все полиномы, чтобы создать перечисление многочленов в рамках которого должны достигнуть каждый полином за полиноминальное время.
. Мы должны перебрать все полиномы, чтобы создать перечисление многочленов в рамках которого должны достигнуть каждый полином за полиноминальное время.
 однозначно определяется относительно всех разумных алгоритмических моделей.
однозначно определяется относительно всех разумных алгоритмических моделей. инвариантен относительно обратной задачи:
инвариантен относительно обратной задачи:  А вот для класса
А вот для класса  Пример: Если проверка выполнимости КНФ решается за полиноминальное время. Для того, чтобы убедится что КНФ не выполнима полиноминальной догадки не существует.
Пример: Если проверка выполнимости КНФ решается за полиноминальное время. Для того, чтобы убедится что КНФ не выполнима полиноминальной догадки не существует. ,
,  - маловероятно. Если
- маловероятно. Если  , то
, то  (дополнение класса
(дополнение класса  до
до  ) - трудно решаемые задачи.
) - трудно решаемые задачи.


