
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свободные и связанные переменныеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Содержание
Введение. 4 1. Алгебра логики (высказывания и предикаты). 8 1.1 Понятие алгебраической системы.. 8 1.2 Примеры алгебраических систем.. 8 1.3 Булевы алгебры.. 9 1.4 Алгебра высказываний. 9 1.5 Алгебра предикатов. 10 1.6 Истинностное значение формулы.. 13 1.7 Отношение следования. 17 1.8 Равносильность. 18 2. Булевы функции и нормальные формы.. 19 2.1 Способы задания. 19 2.2 Унарные и бинарные операции. 21 2.3 Сведение к нескольким операциям.. 22 2.4 Теорема Поста. 22 2.5 Нормальные формы.. 23 2.6 Полиномы Жегалкина. 25 3. Исчисление высказываний. 26 3.1 Общее понятие о логическом исчислении. 26 3.2 Правила вывода исчисления высказываний. 26 3.3 Аксиомы.. 27 3. 4 Доказуемость формул. 27 8. 3.5 Выводимость формул. 27 3.6 Транзитивность секвенций. 28 3.7 Теорема дедукции. 28 3.8 Непротиворечивость исчисления высказываний. 29 3.9 Полнота исчисления высказываний. 29 4. Исчисление предикатов. 30 4.1Теорема дедукции. 31 4.2 Вспомогательные правила вывода. 32 Логические. 32 4.3 Непротиворечивость исчисления предикатов. 34 4.4 Полнота исчисления предикатов. 34 4.5 Другие теоремы.. 36 5. Алгоритмические модели. 37 5.1 Понятие алгоритма. 37 6. Машины Тьюринга. 38 6.1 Описание одноленточной машины Тьюринга. 38 6.2 Функции, вычислимые по Тьюрингу. 39 6.3 Свойства машин Тьюринга. 40 6.4Тезис Тьюринга. 42 7. Частично-рекурсивные функции. 43 7.1 Определение частично-рекурсивных функций. 43 7.2 Примеры ЧРФ.. 44 7.3 Тезис Чёрча. 45 8. Соотношение между классами «Т» и «Ч». 45 8.1 Вычислимость по Тьюрингу ЧРФ.. 45 9. Нумерации наборов чисел и слов. 47 9.1 Нумерация пар чисел. 47 9.2 Наборов из n чисел. 48 9.3 Нумерация множества M=N&N2&….. 48 9. 4 Нумерация слов. 48 10. Нумерация алгоритмов. Невычислимые функции. 48 10.1 Нумерация машин Тьюринга. 48 11. Алгоритмически неразрешимые проблемы.. 51 11.1 Понятие массовой и индивидуальной алгоритмической проблемы. Определение алгоритмически неразрешимой проблемы.. 51 11.2 Способы доказательства алгоритмической неразрешимости. 51 11.3 Проблема « x Î Wx ». 53 11.4 Другие неразрешимые проблемы из теории рекурсивных функций. 54 11.5 Различные примечательные неразрешимые проблемы математики. 54 12. Сложность вычислений. 54 12.1 Характеристики сложности. 54 12.2 Теорема об отсутствии верхней границы сложности вычислений. 56
12.3 Теорема Блюма о линейном ускорении. 56 13 Примеры лёгкорешаемых и труднорешаемых задач. 59 13.1 Класс «NP». 61 14.1 Полиноминальная сводимость задач. 63 14.2 Класс «NPC». 63 14.3 Основные NP-полные задачи. 64
Введение
Логика – наука, изучающая методы доказательства рассуждений и логического вывода Мат. Логика отличается тем, что используются специализированные символьные языки, причём символьный язык может заменить обычный. Различают язык субъекта и объекта, т. е. язык, который изучают и с помощью которого изучают. Логика изучает возможности специализированных языков в 2-х аспектах: · Семантика · Синтаксис Логика делится на: · Теория моделей (семантический подход) · Теория доказательств (синтаксический подход)
Первое логическое учение - силлогистика Аристотеля. Аристотель выделил 4 типа высказываний: · А – общеутвердительные · I – частноутвердительные · E – общеотрицательные · O – частноотрицательные Всё познание состоит в установлении соответствия между разными группами объектов. В силлогистике рассматриваются заключения, которые следуют из двух посылок. 1 – на этом месте одно из 4-х высказываний (A, I, E, O) 2 – на этом месте одно из 4-х высказываний (A, I, E, O) 3 – заключение Можно получить 64 комбинации утверждений в рамках доказательства, но возможны не все сочетания, а только 11 являются корректными: AAA, AAI, AEE, AEO, AII, AOO, EAE, EAO, EIO, IAI, OAO. В остальных случаях при истинных посылках заключение не всегда является истинным. Пример невыполнения: AEA. Не любое разрешенное сочетание является корректным. Чтобы выяснить в каких посылках заключение всегда истинно при истинных посылках, нужно рассмотреть более глубокую структуру. Выделяют 4 фигуры силлогизма.
Пример: Для каждой фигуры есть свой набор сочетаний: 1) AAA, EAE, AII, EIO 2) EAE, AEE, EIO, AOO
3) AAI, EAO, IAI, AII, OAO, EIO 4) AAI, AEE, IAI, AII, OAO, EIO Канторовская теория множеств противоречива Парадокс Рассела Доказательство: Рассмотрим множество S – множество всех множеств, которые не содержат себя в качестве элемента. Предположим, что множество S не содержит себя в качестве элемента Пусть
Парадокс Ришара Назовем фразой любую последовательность букв русского алфавита или знаков припинания и пробел. Примеры: «аб,к н», «а в квадрате». Все фразы могут быть упорядочены в лексикографическом порядке «а,б,в,,…, ххххх, ….». Некоторые фразы—скажем, приведенная выше фраза «а в квадрате»—являются описаниями одноместных арифметических функций на русском языке. Вычеркнем теперь из нашего пересчета все фразы, не являющиеся такого рода описаниями функций; в результате получим пересчет
Парадокс Бери Рассмотрим выражение «наименьшее натуральное число, которое нельзя назвать посредством меньше чем тридцати трех слогов». Это выражение называет некоторое определенное натуральное число—обозначим его через N. Т.к. каждое непустое множество натуральных чисел (в данном случае речь идет о множестве натуральных чисел, которые нельзя назвать посредством меньше чем тридцати трех слогов) имеет наименьший элемент. Согласно своему определению, N нельзя назвать посредством меньше чем тридцати трех слогов. Но ведь наше выражение определяет N, причем с помощью ровно тридцати двух слогов!
Парадокс лжеца «Высказывание, которое я сейчас произношу, ложно». Очевидно, что заключенное в кавычки высказывание не может быть ни истинным, ни ложным. Открытие парадоксов привело к кризису в математике => т.к. математика была сформулирована на теории множеств. Выход был найден с помощью аксиоматического подхода. Задача найти универсального математического робота, который с помощью формальных процедур мог дать результат, который когда-либо могла дать математика. Создаем сигнатуры и какие-то базовые формулы из которых получается все остальные формулы.
Если использую правила вывода можно вывести формулу либо её отрицание, то теория считается полной. Если для формулы нельзя вывести ни формулу, ни отрицание, нужно использовать какую-то более полную теорию. В 1931 Гёдель сформулировал теорему о неполноте. «Всякая достаточно полная теория не полна»
Понятия, характеризующие теорию · Непротиворечивость теории – для любой формулы теории нельзя одновременно доказать формулу и её отрицание · Полнота – для любой формулы можно вывести либо формулу, либо отрицание · Разрешимость – теория называется разрешимой, если для каждой формулы после определенного количества шагов можно сказать является она истинной или ложной. Примеры полных теорий: геометрия, теория векторных пространств.
1. Алгебра логики (высказывания и предикаты) 1.1 Понятие алгебраической системы
Пусть есть множество Тогда декартова n-ая степень множество А есть множество упорядоченных наборов по n элементов
Введём n-местное отношение R на определённом множестве А: Любое подмножество множества А есть отношение. Введём n-местную операцию на множестве А:
Каждому упорядоченному набору соответствует элемент из множества А Алгебраическая система – есть множество из совокупности трёх множеств: · Множество А – является носителем алгебраической системы · ·
Если в алгебраической системе нет отношений то её называют алгеброй Если нет операций то это модель 1.2 Примеры алгебраических систем
· Множество действительных чисел с операциями сложения и умножения {R, ·, +} · Множество целых чисел {Z, ·, +} · Множество рациональных чисел {Q, ·, +} · Множество натуральных чисел {N, ·, +} · Множество векторов С операцией сложения определённой на плоскости
· Алгебра подмножеств:
Множество всех подмножеств множества А. {P(A), C,
- F – полный граф
Есть полный граф. Рассмотрим множество всех его подграфов P(F) введя операции сложения, вычитания и дополнения. {P(F), +, - } “+” – Объединение множества вершин и множества рёбер Сложение и вычитание любых подграфов является подграфом. 1.3 Булевы алгебры Булевой алгеброй называют алгебру на множестве В с операциями +, ·, и констант 0, 1
{В, +, ·,, 0, 1} В – булева алгебра Данные операции должны обладать следующими свойствами: 1. Свойство идемпотентности: а+а=а, а·а=а 2. Свойство коммутативности a+b=b+a, a·b=b·a 3. Свойство ассоциативности (a+b)+c=a+(b+c), a·(b·c)=(a·b) ·c 4. Свойство дистрибутивности a+(b·c)=a+b·a+c, a·(b+c)=a·b+a·c 5. a=a 6. a+0=a, a+1=1, a·0=0, a·1-a Простейшее булево множество: В={0,1} Более сложное: B={00,01,10,11} Определим операции следующим образом: “+”: (a·b)mod2 “·”: (a+b+a·b)mod2 “
1.4 Алгебра высказываний Высказывание – это повествовательное предложение, которое может быть истинным или ложным. Простые высказывания могут объединяться в сложные с помощью пропозициональных связок. Таких связок 5:
1. Конъюнкция
2. Дизъюнкция
3. Импликация
4. Эквивалентность
5. Отрицание
Импликация и эквивалентность могут быть выражены следующим образом
Пример: Если завтра будет солнце мы пойдём купаться = мы не пойдём купаться или будет солнце.
Пример: Завтра мы пойдём купаться только если будет солнце = если завтра будет солнце то мы пойдём купаться и если солнце будет мы пойдём купаться.
Пример: Завтра мы пойдём купаться только если будет солнце = если завтра будет солнце то мы пойдём купаться или если не пойдём купаться то не будет солнца. Свойства операций 1. Коммутативность
2. Ассоциативность
( 3. Дистрибутивность (
Носителем алгебры является множество {истина, ложь} и свойства операций алгебры высказывания совпадают со свойствами операций булевой алгебры. Алгебра высказываний – это булева алгебра. Математическое определение высказывания – это пропозициональная функция отображающая множество Логика высказываний – это булева алгебра, определенная на множестве симантических значений множеств высказываний включающая операции “НЕ”, ”И”, ”ИЛИ”, импликацию, эквивалентность в соответствии с их таблицами истинности 1.5 Алгебра предикатов
Маша любит. __ Некоторое множество
Предикат - высказывательная форма содержащая переменную часть. При постановки в переменную часть переменной из некоторого множества такая высказывательная форма превращается в высказывание, которое может быть истинным или ложным
Y Любит X
Множество, из которого выбираются значения для предиката называться объектным множеством.
Y Любит X Объектное множество
Примеры предикатов: X > 0 X ∈ Z X > Y X, Y ∈ N
n-местный предикат может быть ассоциирован с некоторым подмножеством декартовой степени n, для которого значение предиката истинно
1) К предикатам могут быть применены все те же операции, как и к высказываниям
2) Существует дополнительная операция для предикатов – навешивание кванторов
Примеры A=N
В результате действия квантора арность предиката уменьшается.
Результирующий предикат от конкретного значения х1 не зависит. Переменная, по которой действует квантор, называется связанной, остальные – свободными. Определения и формулы алгебры предикатов Алфавит состоит из: 1) x,y,z – индивидные переменные (применяются для обозначения элементов из основного множества). В общем виде – xi, где i=1,2… Набор пропозициональных букв – A,B,C Набор предикатных букв – Скобки, запятые 2) Определение формулы База индукции: 1) Любая пропозициональная или предикатная буква – формула (А), (Pn(x1…xn)) 2) Если А и В – формулы алгебры предикатов, то (А 3) Если А – произвольная формула алгебры предикатов, х – индивидная переменная, то 4) Других формул нет!
Соглашение о скобках. Любая предикатная и пропозициональная буква должна заключаться в скобки. Следовательно, необходимо писать:
Соответственно, правильными будут являться записи:
При неограниченном применении скобок порядок действий всегда однозначный Для упрощения записи применяется соглашение о старшинстве:
Будем опускать скобки в случае, если порядок действий будет совпадать с приоритетом операций. Также можно опускать внешние скобки над всей формулой. A и (A), также как и Следует заранее обговаривать в каких случаях скобки применяются в одном и том же смысле. Применение скобок и запятых не должно вызывать противоречие. Таблица истинности Для формулы алгебры высказываний можно сказать какие значения она может принимать при конкретных значениях входящих в нее атомов, таким образом, можем построить таблицу истинности
Для формулы алгебры высказываний всегда можем построить такую таблицу. Для формулы алгебры предикатов этого сделать нельзя, т.к.: 1) Не все множества конечны 2) Нас интересуют все возможные множества Однако мы можем построить ограниченную таблицу истинности для частного случая, когда носителем алгебры предикатов является конечное множество: Пример Имеем одноместный предикат Ф(у) и объектное множество A={0,1}
В этом случае имеем 4 варианта формул определения одноместного предиката. Множество упорядоченных пар отображается на булево множество И, Л
{<00>, <01>, <10>, <11>} В случае объектного множества A={0,1, 2} имеем 8 вариантов определения одноместного предиката.
Выполнимость формул В алгебре высказываний формула называется выполнимой, если имеется набор истинности значений атомов, при которых значение формулы истинно. В алгебре предикатов формула выполнима, если существует интерпретация формулы, при которой она истинна.
Множество формул алгебры предикатов называется выполнимым, если существует интерпретация, в которой значения этих формул одновременно истинны. F = (A,B,C) Чтобы доказать, что формула выполнима, необходимо предъявить интерпретацию, в которой она истинна. В алгебре высказываний нужно предъявить строку таблицы истинности, в которой значение формулы истинно. Если ни в одной из интерпретаций формула не принимает истинного значения, то она является невыполнимой. Такая формула называется противоречие. Пример
Ни при каком значении атома А формула не принимает истинного значения Формулы, истинные в любой интерпретации называются общезначимыми или тавтологиями.
В случаем алгебры высказываний общезначимой будет формула, значение которой истинно во всех строках своей таблицы истинности. Примеры Логические законы 1) 2) 3)
В случае алгебры предикатов доказать общезначимость с помощью таблицы истинности нельзя, однако имеются примеры, для доказательства которых необходимо воспользоваться общими рассуждениями 1) Доказательство:
а)
Если предикат является истинным для всех значений индивидной переменной, то формула истинна. Б) Существуют значения индивидных переменных, при которых P(x) будет ложным
2) Доказательство а) Существуют значения индивидных переменных, для которых предикат P(y) истинен, тогда
б) Тогда
Для опровержения общезначимости необходимо привести хотя бы 1 интерпретацию или 1 строку из таблицы истинности, в которой формула ложна. Нахождение всех общезначимых формул – основная задача алгебры логики.
Отношение следования Следование формулы В из формулы А будем обозначать: 1) Формула В следует из формулы А если в любой интерпретации, в которой формула А истинна, формула В также истинна. Пример
Чтобы в этом убедиться, необходимо построить таблицу истинности. 2) Формула А следует из множества формул Г=
(Здесь и далее символ Пример
Убедиться можно аналогично, построив таблицу истинности. Равносильность Равносильность формулы В формуле А будем обозначать: Формула А равносильна формуле В, если Основные формулы равносильности 1) 2) 3) 4) 5)Законы де Моргана
Для алгебры предикатов необходимо добавить закон коммутативности для кванторов
и законы де Моргана для кванторов
Отношение равносильности связано с отношением следования Теорема 2: Необходимость: или
Задание логической функции с помощью таблицы Каждая логическая функция м.б. задана с помошью таблицы. Пример: Задана некая булева функция.
Всего 2n логических наборов переменных. Сколько м.б. различных булевых функций от n переменных? 2n-количество различных упоряд. наборов из n переменных. Логическая функция от n переменных м.б. задана как 2n различных наборов, при этом каждому набору должно соответсвовать одно из двух значений. Таким образом, при n=1, получаем 22=4 лог. Функций f(x).
При n=2,получаем 16 функций.
(x)– константа х (y)– константа y
Константа 0 1 – константа 1
| - штрих Шеффера
Задание логической функции с помощью формулы Логическую функцию можно задать с помощью формул и бинарных операций. Пример: У нас есть некая бинарная функция и.
Если вместо одной из переменных поставить любую бинарную функция, то получим функцию от 3-х переменных. Вывод:любая функция может быть задана как таблицей, так и формулой.
Унарные и бинарные операции Рассмотрим свойства унарных и бинарных операций: Коммутативность Коммутативными называют логические функции или логические операции, если они обладают следующим свойством: x # x = y # x, где # - &, v, ~, |, ↓, +
Ассоциативность
(x # y) # z = x # (y # z), где # - &, v, ~, +
Дистрибутивность x # (y Ъ z) = (x # y) Ъ (x # z), где #,Ъ - (&, v), (v,&),(&, +)
Обратные операции (x#y)=xЪy, где #,Ъ - (&,|), (v,↓), (>,→), (<,←), (~,+) Бинарное отрицание меняет логическую операцию на обратную.
Теорема Поста
Введем 5 различных классов функций: 1) F0 – функции сохраняющие «0».
При н
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 564; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.190.25.139 (0.016 с.) |

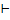
 ............ 27
............ 27 Пример: все натуральные числа являются целыми.
Пример: все натуральные числа являются целыми. Пример: некоторые люди — студенты
Пример: некоторые люди — студенты Пример: ни один из китов не рыба
Пример: ни один из китов не рыба Пример: некоторые люди не являются студентами
Пример: некоторые люди не являются студентами
 но т.к. S мн. всех мн-в не содержащих себя в качестве элемента =>
но т.к. S мн. всех мн-в не содержащих себя в качестве элемента => 
 , но т.к. множество всех множеств, которые не содержат себя в качестве элемента =>
, но т.к. множество всех множеств, которые не содержат себя в качестве элемента =>  . Получаем противоречие
. Получаем противоречие 
 всех таких описаний. Обозначим функции, описываемые этими фразами, соответственно через
всех таких описаний. Обозначим функции, описываемые этими фразами, соответственно через 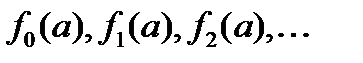 Рассмотрим теперь следующую фразу: «Функция, значение которой для любого данного натурального числа а в качестве аргумента равно увеличенному на единицу значению для этого же аргумента той функции, которая определяется фразой, соответствующей в только что упомянутом пересчете этому натуральному числу». Мы могли бы заменить в этой фразе ее кусок «в только что упомянутом пересчете» исчерпывающим описанием точной конструкции этого самого пересчета, так что в результате из всей нашей фразы получилась бы некоторая другая фраза Р, полностью описывающая ту же самую функцию. Эта фраза Р описывает некоторую арифметическую функцию, а именно
Рассмотрим теперь следующую фразу: «Функция, значение которой для любого данного натурального числа а в качестве аргумента равно увеличенному на единицу значению для этого же аргумента той функции, которая определяется фразой, соответствующей в только что упомянутом пересчете этому натуральному числу». Мы могли бы заменить в этой фразе ее кусок «в только что упомянутом пересчете» исчерпывающим описанием точной конструкции этого самого пересчета, так что в результате из всей нашей фразы получилась бы некоторая другая фраза Р, полностью описывающая ту же самую функцию. Эта фраза Р описывает некоторую арифметическую функцию, а именно  . Следовательно, Р входит в пересчет
. Следовательно, Р входит в пересчет  Но это невозможно, так как функция, описываемая фразой
Но это невозможно, так как функция, описываемая фразой  , отличается от функции, описываемой фразой
, отличается от функции, описываемой фразой  , своим значением для
, своим значением для  от функции, описываемой
от функции, описываемой  значением для
значением для  ; от функции, описываемой
; от функции, описываемой  , значением для
, значением для  и т. д. Оформим это рассуждение иначе. Поскольку фраза
и т. д. Оформим это рассуждение иначе. Поскольку фраза  входит в пересчет
входит в пересчет  , то она имеет в нем некоторый номер
, то она имеет в нем некоторый номер 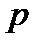 . Значит, подставляя сюда
. Значит, подставляя сюда  вместо
вместо  и сравнивая с предыдущим равенством, приводим к противоречию.
и сравнивая с предыдущим равенством, приводим к противоречию.
 где
где 
 - Упорядоченный набор. Причём порядок в наборе имеет значение т.е.
- Упорядоченный набор. Причём порядок в наборе имеет значение т.е. 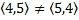


 - нольместая операция, есть const равная одному из элементов множества
- нольместая операция, есть const равная одному из элементов множества - Множество отношений определённых на множестве А
- Множество отношений определённых на множестве А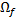 - Множество операций определённых на множестве А
- Множество операций определённых на множестве А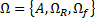 , где
, где  ,
, 


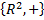 , (a, b)
, (a, b) 
 , a, b
, a, b 
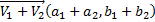

 } – алгебра
} – алгебра ”: (a+1)mod2
”: (a+1)mod2










 т.е.
т.е. 


 значения определяются в соответствии с таблицей
значения определяются в соответствии с таблицей – квантор всеобщности (результат истинный, если значение предиката истинно по всем переменным)
– квантор всеобщности (результат истинный, если значение предиката истинно по всем переменным) – квантор существования (результат истинный, если среди элементов объектного множества существует такой элемент, при котором предикат принимает истинное значение)
– квантор существования (результат истинный, если среди элементов объектного множества существует такой элемент, при котором предикат принимает истинное значение)



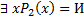


 , где n – арность предикатной буквы, n>0, а j – индекс, j>0
, где n – арность предикатной буквы, n>0, а j – индекс, j>0 В), (А
В), (А 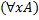 ,
,  - формулы алгебры предикатов
- формулы алгебры предикатов



 Старшая операция находится левее
Старшая операция находится левее ,
,  и
и  – это, в общем случае, разные вещи.
– это, в общем случае, разные вещи.

 {И, Л}
{И, Л}



 – закон отрицания отрицания
– закон отрицания отрицания – закон отрицания противоречия
– закон отрицания противоречия – закон исключенного третьего
– закон исключенного третьего
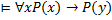


 для
для  , т.е.
, т.е. 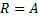

 также истинно, т.к.
также истинно, т.к.  истинно при любых значениях объектных переменных
истинно при любых значениях объектных переменных имеем импликацию вида И
имеем импликацию вида И 

 т.к. ложная посылка импликацию дает истину.
т.к. ложная посылка импликацию дает истину.


 , т.к. заключение истинно
, т.к. заключение истинно , для
, для 



 если во всех интерпретациях, в которых формулы
если во всех интерпретациях, в которых формулы  истинны, формула А также истинна.
истинны, формула А также истинна. 
 , …
, …  И
И будет соответствовать словесной формулировке «если…, то…»)
будет соответствовать словесной формулировке «если…, то…»)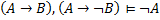
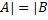
 в любой интерпретации I. В случае логики высказываний формулы равносильны, если их таблицы истинности одинаковы, что используется для доказательства равносильности.
в любой интерпретации I. В случае логики высказываний формулы равносильны, если их таблицы истинности одинаковы, что используется для доказательства равносильности. – идемпотентность
– идемпотентность ,
, 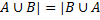 – коммутативность
– коммутативность – ассоциативность
– ассоциативность – дистрибутивность
– дистрибутивность





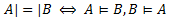



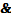





 x – отрицание х
x – отрицание х  - конъюнкция
- конъюнкция  – Дизъюнкция
– Дизъюнкция - Импликация
- Импликация  - эквивалентность
- эквивалентность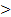 - сравнение x>y
- сравнение x>y 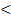 - сравнение x<y
- сравнение x<y - исключающее или
- исключающее или  - обратная импликация
- обратная импликация - стрелка Пирса
- стрелка Пирса

 :
:



