
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Другие неразрешимые проблемы из теории рекурсивных функцийСодержание книги
Поиск на нашем сайте
· Принадлечит ли произвольное число Y области определения ЧРФ под номером X. · Проблема определения принадлечит ли функция в ряду ЧРФ под номером X классу общерекурсивных функций. · Проблема определения, является ли функция под номером X является нуль-функцией. · · Проблема определения обладает ли ЧРФ под номером Х произвольным свойством(монотонность, неотрицательность и др.)
Различные примечательные неразрешимые проблемы математики 1. Формула в элементарной арифметике состоит из:
Т.е. записи вида: Проблема заключается в том чтобы для любой произвольной формулы сказать является ли она истиной или нет. 2. Разрешимость логики предикатов первого порядка. Является ли формула логики предикатов - Е истинной? 3. Проблема сочитаемости Поста Даны алфавит PQ называются сочетаемыми если существует такой набор Проблема состоит в том является ли произвольное множество пар слов сочетаемым. 4. Проблема представимости матриц Представима ли матрица U в базисе Cущес твует ли такой набор В этом случае рассматриваются 5. Проблема тождества элементарных функций вещественного переменного. Т.е. функций:
6. Lесятая проблема Гильберта. Проблема разрешимости в целых числах диофантового уравнения. Задано диофантово уравнение (т.е. уравнение вида:
Сложность вычислений Характеристики сложности Пусть есть машина Тьюринга – Т, которая вычисляет функцию f(x)
Мерой сложности является каличество шагов вычисления. Определим функцию
Активной зоной при работе машины Т на слове X называется множество всех ячеек ленты, которые содержат непустые символы, либо посещались в процессе вычисления f(x) головкой машины Т. Определим функцию
Пусть машина Тьюринга Т имеет внешний и внутренний алфавит мощности k и r соответсвенно. Тогда для функций сложности
Покажем это: В начальный момент на ленте записано слово x длины Найдём теперь число различных конфигураций Далее, если в процессе работы машины встретятся две одинаковые конфигурации, то машина зациклиться, поскольку конфигурация однозначно определяет следующую за ней. Значит, если машина в процессе вычисления использует зону Вводятся функции временной и емкостной сложности по худшему случаю:
Отметим свойства мер сложностей: 1)
Т.е. области определения совпадают 2) Предикаты вида P(x,y) определенные соотшениями Т.е. существует машина Т разрешающая предикаты В начале на ленте написано слово x, считаем количество шагов y до того как на ленет будет написано f(x): если машина остановится значит y, если не осановится то не y. Таким образом всегда можно сказать, что функция f(x) имеет значение y или не имеет. Определение абстрактной мерой сложности. Под абстрактной мерой сложности будем понимать любое семейство функций 1) 2) Преликат
|
||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 435; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.141 (0.006 с.) |

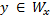
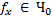

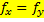

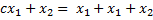
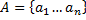 и множество пар слов
и множество пар слов  в алфавите А. И
в алфавите А. И 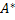 - множество конечных слов в алфавите А.
- множество конечных слов в алфавите А.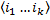 так что
так что 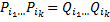

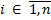 так чтобы
так чтобы 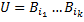
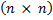 – матрицы и неразрешимость данной проблемы начинается с n=4
– матрицы и неразрешимость данной проблемы начинается с n=4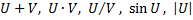 и функции полученные суперпозицией этих функций.
и функции полученные суперпозицией этих функций.
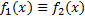 ? – Являются ли функции тождественными
? – Являются ли функции тождественными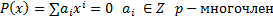 ) с произвольными неизвестными и целыми коэффициентами. Необходимо установить, разрешимо ли уравнение после конечного числа операций в целых числах.
) с произвольными неизвестными и целыми коэффициентами. Необходимо установить, разрешимо ли уравнение после конечного числа операций в целых числах.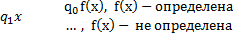
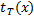 , равную числу шагов до остановки - n машины Т, выполненному при вычислении f(x), если f(x) определена. Если f(x) не определена, то значение
, равную числу шагов до остановки - n машины Т, выполненному при вычислении f(x), если f(x) определена. Если f(x) не определена, то значение 
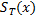 , равную длине активной зоны при работе машины Т на слове X, если f(x) определена. Если f(x) не определена, то значение
, равную длине активной зоны при работе машины Т на слове X, если f(x) определена. Если f(x) не определена, то значение 
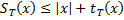
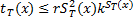
 . На каждом шаге активной становится не более одной новой ячейки, поэтому
. На каждом шаге активной становится не более одной новой ячейки, поэтому 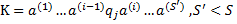 с активной зоной
с активной зоной 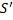 . Имеется
. Имеется 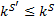 вариантов записи на ленте, r вариантов выбора положения головки и S вариантов для значения длины
вариантов записи на ленте, r вариантов выбора положения головки и S вариантов для значения длины 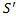 конфигурации К. Таким образом, число рассматриваемых конфигураций не превосходит
конфигурации К. Таким образом, число рассматриваемых конфигураций не превосходит 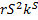 .
.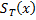 , то число её шагов не превосходит числа различных конфигураций с зоной не превышающей
, то число её шагов не превосходит числа различных конфигураций с зоной не превышающей 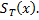 В итоге получаем неравенство
В итоге получаем неравенство 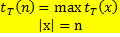
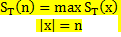
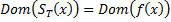
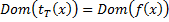
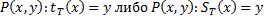 является разрешимым.
является разрешимым.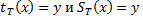
 которое обладает свойствами:
которое обладает свойствами:
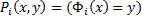 – разрешим
– разрешим


