
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Правила вывода исчисления высказыванийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Будем использовать 2 правила вывода: a. Правило отдаления (modus ponens): b. Правило подстановки (S):
Аксиомы 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. Если вместо пропозициональных букв будем использовать любую формулу исчисления высказываний, то можем получить бесконечное множество аксиом заданной структуры (схем аксиом). Доказуемость формул Доказательством формулы Пример доказательства формулы:
8. Выводимость формул Секвенцией (выводом из посылок)
Пример:
Возникает вопрос: Можем ли мы вместо С подставить любую формулу? Ответ: Нельзя, правило подстановки имеют ограничение, его нельзя применять к пропозициональным буквам, которые содержатся в формулах, введенных в качестве посылок. Транзитивность секвенций Теорема 1: Правило силлогизма Если существуют выводы
Доказательство: Вывод Теорема дедукции Теорема 2: Теорема дедукции. Импликация
Доказательство: Необходимость: Пусть формула
Достаточность: не будем рассматривать в силу громоздкости вывода.
Непротиворечивость исчисления высказываний Теорема 3: Теорема об общезначимости доказуемых формул. Если формула доказуема, то она общезначима.
Доказательство: Пусть есть некоторая последовательность формул Следствие 1: О непротиворечивости исчисления высказывания Ни для какой формулы из исчисления высказываний не может быть доказана и сама формула и её отрицание.
Доказательство: Предположим, что формула Полнота исчисления высказываний Теорема 4: Теорема о полноте исчисления высказываний Если формула общезначима, то она доказуема
Следствие 1: Если к системе аксиом ИВ добавить произвольную формулу !Нельзя усилить ИВ добавлением недоказуемой формулы к системе аксиом. Из теорем 3 и 4 следует: Получили эквивалентность синтаксического и семантического подхода в рамках исчисления высказываний.
Исчисление предикатов Для того чтобы задать исчисление предикатов необходимо задать: Язык (алфавит). Он совпадает с языком логики и включает в себя: пропозициональные буквы, предикатные буквы, пропозициональные переменные и формулы. 2. Аксиомы. Аксиомы исчисления высказываний актуальны для исчисления предикатов. Чаще используются схемы аксиом: a. b. c. Правила вывода Дополнительные правила вывода 1. Правило всеобщности. Покажем справедливость данного правила:
Правила вывода должны быть корректными (при истинных посылках, истинные следствия) Тогда имеем 1. Пусть 2. Пусть 2. Правило существования ( Покажем справедливость данного правила: Имеем 1. Пусть 2. Пусть
Дадим определения доказательства и вывода. Доказательство формулы Вывод формулы Примечание: Дополнительные правила вывода нельзя применять к переменным, которые были введены в качестве посылки. Такие переменные называются фиксированными переменными.
Пример вывода: Выведем, что
Теорема дедукции
Необходимость Пусть Достаточность
Это доказательство мы опустив в связи с его громоздкостью. Теорема: Правило силлогизма Если Используем теорему о дедукции
Тогда имеем вывод Теорему о дедукции и правило силлогизма можно записать в виде вспомогательных правил вывода. Вспомогательные правила вывода используются для доказательства значения факта, что вывод или доказательство существует.
Если существует вывод, записанный сверху, то существует вывод записанный снизу.
|
||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 2173; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.232.171 (0.01 с.) |


 Каждую букву заменяем на формулу. Конечная формула будет истинна, если для подстановки использовались общезначимые формулы (берем общезначимую формулу и заменяем в ней каждую букву на формулу)
Каждую букву заменяем на формулу. Конечная формула будет истинна, если для подстановки использовались общезначимые формулы (берем общезначимую формулу и заменяем в ней каждую букву на формулу)

 - правило введения
- правило введения 
 - правило удаления
- правило удаления 
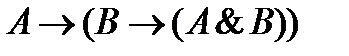 - правило введения
- правило введения 
 - правило удаления &
- правило удаления & - правило введения
- правило введения 
 - правило удаления
- правило удаления  - правило введения
- правило введения 
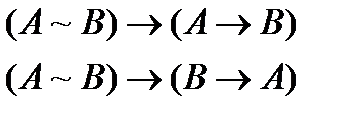 - правило удаления
- правило удаления  является некоторая последовательность формул
является некоторая последовательность формул 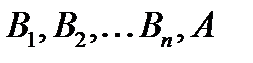 , каждая из которых является либо аксиомой, либо получена применением одного из правил вывода, а в конце последовательности стоит формула
, каждая из которых является либо аксиомой, либо получена применением одного из правил вывода, а в конце последовательности стоит формула  .
.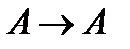
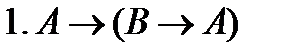 - по первой аксиоме
- по первой аксиоме - используем подстановку
- используем подстановку 
 - по второй аксиоме
- по второй аксиоме - подстановка
- подстановка 

 - подстановка в формулу 1
- подстановка в формулу 1 
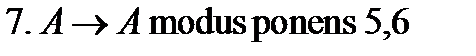
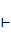

 называется последовательность формул
называется последовательность формул  , где
, где  - либо аксиома, либо получена по правилу вывода, либо
- либо аксиома, либо получена по правилу вывода, либо  , где
, где  - множество посылок вывода.
- множество посылок вывода.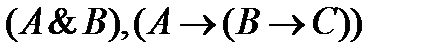
 (вывод
(вывод  из посылок
из посылок  )
) - аксиома удаления &
- аксиома удаления & - первая посылка
- первая посылка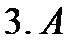 - modus ponens 1.2
- modus ponens 1.2 - аксиома удаления &
- аксиома удаления & - первая посылка
- первая посылка - modus ponens 4,5
- modus ponens 4,5 - вторая посылка
- вторая посылка - modus ponens 3,7
- modus ponens 3,7 - modus ponens 6,8
- modus ponens 6,8
 , то существует вывод
, то существует вывод 

 - означает, что есть последовательность формул
- означает, что есть последовательность формул  . Вывод
. Вывод  - означает, что есть последовательность формул
- означает, что есть последовательность формул  . Запишем два вывода последовательно
. Запишем два вывода последовательно  , полученная запись и есть вывод
, полученная запись и есть вывод  .
. доказуема тогда и только тогда, когда формула
доказуема тогда и только тогда, когда формула  выводима из
выводима из  .
. 
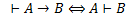
 . Добавим
. Добавим  в качестве посылки:
в качестве посылки:  получили
получили 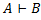 .
.
 , где
, где  является либо аксиомой, либо получена из правил вывода. Каждая формула в последовательности является общезначимой
является либо аксиомой, либо получена из правил вывода. Каждая формула в последовательности является общезначимой 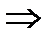 все формулы в последовательности являются общезначимыми
все формулы в последовательности являются общезначимыми  формула
формула  общезначима.
общезначима.
 доказуема
доказуема  это означает, что она общезначима
это означает, что она общезначима  . Общезначимая формула в любой интерпретации истинна
. Общезначимая формула в любой интерпретации истинна  . Теперь рассмотрим формулу
. Теперь рассмотрим формулу  , она будет ложна в любой интерпретации
, она будет ложна в любой интерпретации  это означает, что
это означает, что  не общезначима
не общезначима 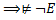 . По теореме об общезначимости
. По теореме об общезначимости  .
.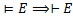
 , которая не является общезначимой
, которая не является общезначимой 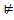
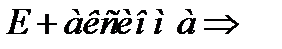 найдется
найдется  , для которой будет существовать
, для которой будет существовать 


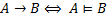

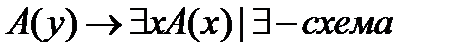
 Замена возможна, если индивидные переменные не входят в формулу свободно.
Замена возможна, если индивидные переменные не входят в формулу свободно. , где С – формула исчисления предикатов, х – не входит свободно в С. Тогда можно записать
, где С – формула исчисления предикатов, х – не входит свободно в С. Тогда можно записать  .
.
 тогда
тогда  должно быть Истинно при всех
должно быть Истинно при всех 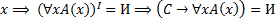
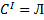 тогда
тогда  при любых
при любых 
 ).
).  , если х не входит свободно в С, то мы можем записать
, если х не входит свободно в С, то мы можем записать 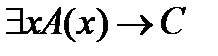



 – это некоторая последовательность формул
– это некоторая последовательность формул  которая заканчивается формулой
которая заканчивается формулой  , причем формулы
, причем формулы  являются аксиомами или формулами выведенными с помощью правил вывода.
являются аксиомами или формулами выведенными с помощью правил вывода. из множества формул Г – это некоторая последовательность формул
из множества формул Г – это некоторая последовательность формул  , причем формулы
, причем формулы 

 - фиксированные переменные.
- фиксированные переменные.
 - допущение
- допущение - аксиома всеобщности
- аксиома всеобщности - modus ponens 1,2
- modus ponens 1,2 - аксиома всеобщности
- аксиома всеобщности - modus ponens 3,4
- modus ponens 3,4
 - формулы исчисления предикатов
- формулы исчисления предикатов  - множество формул исчисления предикатов
- множество формул исчисления предикатов тогда имеем вывод
тогда имеем вывод  где
где 
 . Далее запишем
. Далее запишем  в качестве посылки и применим правило отделения
в качестве посылки и применим правило отделения 
 то существует вывод
то существует вывод  где
где  - формулы ИП
- формулы ИП
 используя правило отделения получим
используя правило отделения получим 
 - правило введения импликации (из теоремы о дедукции)
- правило введения импликации (из теоремы о дедукции) – правило силлогизма
– правило силлогизма


