
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Система аксиом исчисления высказыванийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Одним из возможных вариантов (Гильбертовской) аксиоматизации логики высказываний является следующая система аксиом:
вместе с единственным правилом:
Теорема корректности исчисления высказываний утверждает, что все перечисленные выше аксиомы являются тавтологиями, а с помощью правила modus ponens из истинных высказываний можно получить только истинные. Доказательство этой теоремы тривиально и сводится к непосредственной проверке. Куда более интересен тот факт, что все остальные тавтологии можно получить из аксиом с помощью правила вывода — это так называемая теорема полноты логики высказываний.
18. Правило вывода Modus ponens. Modus ponens (правило заключения): если A и A→B — выводимые формулы, то B также выводима. Форма записи: Modus ponens — правило вывода в исчислении высказываний. Является частным случаем правила резолюций. С помощью правила modus ponens из истинных высказываний можно получить только истинные. Доказательство этой теоремы тривиально и сводится к непосредственной проверке. Куда более интересен тот факт, что все остальные тавтологии можно получить из аксиом с помощью правила вывода — это так называемая теорема полноты логики высказываний. Понятие вывода. Определение. Выводом из конечной совокупности формул H называется всякая конечная последовательность формул Свойства вывода: 1) Всякий начальный отрезок вывода из совокупности H есть вывод из H. 2) Если между двумя соседними членами вывода из H вставить некоторый вывод из H, то полученная новая последовательность формул будет выводом из H. 3) Всякий член вывода из совокупности H, является формулой, выводимой из H. Следствие. Всякий вывод из H является выводом его последней формулы. 4) Если 5) Для того, чтобы формула B была выводима из совокупности H, необходимо и достаточно, чтобы существовал вывод этой формулы из H.
Понятие вывода
ками вывода. Свойства:
23. Теорема о дедукции Лемма Кальмара
29. Теорема полноты исчисления высказывний.
Формулы исчисления предикатов
Сигнатура, алгебры и модели. Сигнатурой называется набор Σ = (R, F, C,ρ) состоящий из множеств: R — множество символов для отношений (предикатов), F — множество функциональных символов, C — множество символов констант и функции ρ — сопоставляющей элементам R и F их арность. Пример σ=<+,*,<,=,1>
Формальная система исчисления предикатов. Язык логики первого порядка строится на основе сигнатуры, состоящей из множества функциональных символов Символы переменных (обычно Пропозициональные связки: Кванторы: всеобщности Служебные символы: скобки и запятая. Перечисленные символы вместе с символами из Терм есть символ переменной, либо имеет вид Атом имеет вид Формула — это либо атом, либо одна из следующих конструкций: Переменная
Система аксиом исчисления предикатов.
|
|||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 669; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.212.245 (0.01 с.) |

 ;
;
 ;
; ;
; ;
;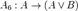 ;
; ;
;
 ;
;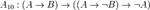 ;
;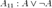 .
. (Modus ponens)
(Modus ponens) , где A, B — любые формулы.
, где A, B — любые формулы. , всякий член которой удовлетворяет одному из следующих трех условий: 1) является одной из формул совокупности H; 2) является доказуемой формулой; 3) получается по правилу заключения из двух любых предшествующих членов последовательности
, всякий член которой удовлетворяет одному из следующих трех условий: 1) является одной из формул совокупности H; 2) является доказуемой формулой; 3) получается по правилу заключения из двух любых предшествующих членов последовательности  .
. , то всякий вывод из H является из W.
, то всякий вывод из H является из W.


















 и множества предикатных символов
и множества предикатных символов  . С каждым функциональным и предикатным символом связана арность, то есть число возможных аргументов. Допускаются как функциональные, так и предикатные символы арности 0. Первые иногда выделяют в отдельное множество констант. Кроме того, используются следующие дополнительные символы
. С каждым функциональным и предикатным символом связана арность, то есть число возможных аргументов. Допускаются как функциональные, так и предикатные символы арности 0. Первые иногда выделяют в отдельное множество констант. Кроме того, используются следующие дополнительные символы и т. д.),
и т. д.), ,
, и существования
и существования  ,
, образуют Алфавит логики первого порядка. Более сложные конструкции определяются индуктивно:
образуют Алфавит логики первого порядка. Более сложные конструкции определяются индуктивно: , где
, где  — функциональный символ арности
— функциональный символ арности  , а
, а  — термы.
— термы. , где
, где  — предикатный символ арности
— предикатный символ арности  — термы.
— термы. , где
, где 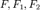 — формулы, а
— формулы, а  — переменная.
— переменная. называется связанной в формуле
называется связанной в формуле  , если
, если  имеет вид
имеет вид  либо
либо  , или же представима в одной из форм
, или же представима в одной из форм  , причем
, причем 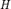 ,
,  и
и  . Если
. Если  не связанна в
не связанна в  , ее называют свободной в
, ее называют свободной в 




