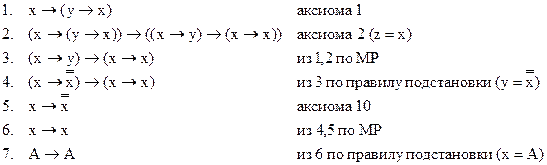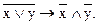Тема 4. Исчисление высказываний

ТЕМА 4. ИСЧИСЛЕНИЕ ВЫСКАЗЫВАНИЙ

ЯЗЫК, АКСИОМЫ И ПРАВИЛА ВЫВОДА ИСЧИСЛЕНИЯ ВЫСКАЗЫВАНИЙ

1. Общее понятие о формальной аксиоматической теории.
2. Алфавит, формулы и подформулы исчисления высказываний.
3. Система аксиом исчисления высказываний. Основные правила вывода.
4. Определение доказуемой (выводимой) формулы. Примеры доказательств.
5. Производные правила вывода.

Введение

Исторически понятие формальной теории было разработано в период интенсивных исследований в области оснований математики для формализации собственно логики и теории доказательств. Сейчас этот аппарат широко используется при создании специальных исчислений для решения конкретных прикладных задач.

Таблицы истинности в алгебре высказываний позволяют ответить на многие вопросы, касающиеся логики высказываний. Однако более сложные вопросы логики высказываний уже не могут быть решены с помощью таблиц истинности.

Давая описание алгебры высказываний, мы пользовались логическими значениями высказываний (истина, ложь). Но понятия истинности и ложности не являются математическими. Эти понятия во многих случаях субъективны и скорее относятся к методологии познания. В связи с этим желательно построить теорию, не пользуясь понятиями истинности и ложности, не применяя законов логики. Такой теорией, в частности, является исчисление высказываний, которое строится по общим правилам построения формальных аксиоматических (дедуктивных) теорий (или исчислений).

Вопрос 1. Общее понятие о формальной аксиоматической теории

Математическая наука достигает совершенства лишь тогда, когда ей удается пользоваться аксиоматическим методом, т.е. когда наука принимает характер аксиоматической теории. Более того, развитие наук в ХХ веке показало, что математика выделяется в системе наук тем, что в ней чрезвычайно широко используется аксиоматический метод, который в значительной мере и обуславливает поразительную эффективность математики в процессе познания окружающего мира и преобразующего воздействия на него.

Аксиоматический метод базируется на простых отношениях между символами и выражениями точных формальных языков и использует достаточно простые арифметические методы. Это обстоятельство обеспечивает надежность аксиоматического метода.

О.1.1. Под аксиоматической теорией, построенной на основе данной системы аксиом, понимается совокупность всех теорем, доказываемых исходя из этой системы аксиом.

Аксиоматические теории делятся на формальные и неформальные теории.

Неформальные аксиоматические теории наполнены теоретико-множественным содержанием, понятие выводимости в них довольно расплывчато и в значительной степени опирается на здравый смысл.

Формализация аксиоматической теории состоит в том, что аксиомы рассматриваются как формальные последовательности символов (выражения) некоторого алфавита, а методы доказательства – как методы получения одних выражений из других с помощью операций над символами. При этом не допускается пользоваться какими-либо предположениями об объектах теории, кроме тех, которые сформулированы явно в аксиомах. Такой подход гарантирует четкость исходных утверждений и однозначность выводов.

Формальные теории называются исчислениями.

Может создаться впечатление, что осмысленность и истинность в формальной теории не играют никакой роли. Внешне это так. Тем не менее, в действительности и аксиомы, и правила вывода стремятся выбирать таким образом, чтобы построенной с их помощью формальной теории можно было придать содержательный смысл.

О.1.2. Формальная аксиоматическая теория Т считается определенной, если выполнены следующие условия:

1. Задан алфавит теории Т, представляющий собой некоторое счетное множество символов. Конечные последовательности символов алфавита теории Т называются словами или выражениями данной теории.
2. Имеется подмножество выражений теории Т, называемых формулами теории Т. Обычно имеется эффективная процедура, позволяющая по данному выражению определить, является ли оно формулой.
3. Выделено некоторое множество формул теории Т, называемых аксиомами. Обычно имеется эффективная процедура, позволяющая по данной формуле определить, является ли она аксиомой.
4. Имеется конечное множество Р₁,Р₂,…,Р_n отношений между формулами, называемых правилами вывода. При этом для каждого Р_i (i = 1, 2, …, n) существует целое положительное число j такое, что для каждого множества, состоящего из j формул, и для каждой формулы А эффективно решается вопрос о том, находятся ли данные j формул в отношении Р_i с формулой А. Если да, то А называется непосредственным следствием данных j формул по правилу Р_i.

О.1.3. Выводом в теории Т называется всякая последовательность формул В₁, В₂, …, В_n данной теории такая, что для любого i (i = 1, 2, …, n) формула В_i есть либо аксиома теории Т, либо непосредственное следствие каких-либо предыдущих формул по одному из правил вывода.

О.1.4. Формула А называется теоремой теории Т (выводимой в Т или доказуемой в Т), если существует вывод в Т, в котором последней формулой является формула А. Такой вывод называется выводом формулы А или доказательством теоремы А.

Алфавит и множество слов (выражений) формальной аксиоматической теории Т образуют язык данной теории, который называется предметным или формальным языком. Предметный язык используется для формулировки высказываний внутри самой формальной теории Т.

Язык, на котором ведется описание формальной аксиоматической теории Т, называется метаязыком. Метаязык используется для формулировок утверждений о формальной теории Т и является языком метатеории, с помощью которой изучается данная формальная аксиоматическая теория Т.

О.1.5. Математическая теория, изучающая данную формальную аксиоматическую теорию Т как единое целое, устанавливающая свойства данной теории Т, называется метатеорией по отношению к изучаемой теории Т.

Факты, устанавливаемые в метатеории относительно изучаемой формальной аксиоматической теории Т, называются метатеоремами (чтобы отличить их от собственно теорем рассматриваемой теории Т).

Формальные аксиоматические теории создаются для того, чтобы описать определенные явления окружающего мира, т.е. реальности (либо конкретной, либо математической). Для установления взаимосвязи между объектами формальной аксиоматической теории Т и объектами реальности вводится понятие интерпретации теории Т.

Интерпретация формальной аксиоматической теории Т подразумевает придание конкретного смысла каждому символу теории Т и устанавливает взаимно-однозначное соответствие между символами теории Т и реальными объектами.

Процесс изучения реальности с помощью формальных аксиоматических теорий можно описать следующим образом:

1. Вначале изучается реальность и конструируется некоторое абстрактное представление о ней, т.е. некоторая формальная теория.

2. Строится доказательство теорем формальной теории. Вся польза и удобство формальных теорий заключаются в их абстрагировании от конкретной реальности. Благодаря этому одна и та же формальная теория может служить моделью многочисленных конкретных ситуаций.

3. Происходит возвращение к начальной точке всего построения и осуществляется интерпретация теорем, полученных при формализации.

Применим аксиоматический подход к алгебре высказываний и построим соответствующую формальную аксиоматическую теорию – исчисление высказываний.

Вопрос 3. Система аксиом исчисления высказываний. Основные правила вывода

Следующим шагом в построении ИВ будет выделение некоторого класса формул, которые называются исходными доказуемыми (выводимыми) формулами или аксиомами ИВ.

Одна из возможных систем аксиом ИВ состоит из 11 аксиом, которые делятся на четыре группы:

I группа

II группа

III группа

IV группа

Все аксиомы I группы из логических связок содержат только импликацию. Эта связка входит и во все остальные группы, но во II группе к импликации присоединяется конъюнкция, в III группе - дизъюнкция, а в IV группе – отрицание.

Основные правила вывода

Одной из основных задач ИВ является выявление того факта, что из множества высказываний (формул) логически следует некоторое другое высказывание (формула).

Определение доказуемых формул имеет тот же характер, что и определение формулы. После введения исходных доказуемых формул (аксиом) определяются основные правила вывода, которые позволяют из имеющихся доказуемых формул получать новые доказуемые формулы.

Образование доказуемой формулы из исходных доказуемых формул путем применения правил вывода, называется логическим выводом данной формулы, доказательством или логическим следствием.

Правило подстановки

Если формула А доказуема в исчислении высказываний, х – переменная, В - произвольная формула исчисления высказываний, то формула, полученная в результате замены в формуле А переменной х всюду, где она входит, формулой В, является так же доказуемой формулой.

Схематично правило подстановки записывается так

├ А(х). (2)

├ А(В)

Формулы, используемые в правилах (1) и (2), называются метаформулами или схемами формул.

Замечание

Смысл метаформул состоит в том, что они обозначают множество всех формул исчисления, которые получаются, если ее метапеременные заменить формулами исчисления. Использование схем формул можно распространить и на аксиомы (но в этом случае для построения исчисления правило подстановки не нужно).

Уточним правило подстановки.

1. Если формула А есть переменная х, то подстановка (2) дает формулу В.

2. Если формула А есть переменная у ¹ х, то подстановка (2) дает формулу А.

3. Если А – формула, для которой подстановка уже определена, то подстановка В вместо х в отрицание формулы А есть отрицание подстановки.

4. Если А₁ и А₂ – формулы, для которых подстановки уже определены, то

├ А₁ * А₂

______________,

├ А₁(В) * А₂(В)

где под символом * понимается любая из логических связок Ù, Ú, →.

Вопрос 4. Определение доказуемой (выводимой) формулы. Примеры доказательств

О.4.1. Выводом называется любая конечная последовательность формул В₁,В₂,…,В_n такая, то для любого i (i = 1, 2, …, n) формула В_i есть либо аксиома, либо совпадает с какой-либо предыдущей формулой, либо получается из каких-то предыдущих формул с помощью одного из правил вывода.

О.4.2. Формула А называется доказуемой (выводимой, теоремой), если существует вывод, в котором последней формулой является А. Обозначение: ├ А.

О.4.3. Процесс получения доказуемой формулы А называется ее доказательством.

Другими словами, доказательство формулы А – построение вывода, в котором последней формулой является формула А.

Замечание

В дальнейшем будем употреблять сокращенный вывод, когда в качестве В_i могут стоять теоремы ИВ, полученные раньше, имея в виду, что мы всегда можем дополнить вывод, вставляя недостающие его отрезки.

Рассмотрим примеры доказательств.

Пример 4. Доказать, что ├ А → А (рефлексивность импликации).

Доказательство

Т.4.1. Для любой формулы А исчисления высказываний формула А → А является теоремой, т.е. доказуема.

Пример 5. Доказать, что ├

Доказательство

Правило сложного заключения

Если формулыА₁, А₂, …, А_n и А₁→ (А₂ → (А₃ → (…(А_n → L) …))) доказуемы, то и формула L доказуема.

Замечание

Правила одновременной подстановки и сложного заключения являются естественным обобщением соответственно правил подстановки и заключения на случай n формул.

Правило силлогизма

Если доказуемы формулы А → В и В → С, то доказуема формула А → С, т.е.

├ А → В,├ В→ С.

├ А → С

Заключение

Рассмотренные вопросы, относящиеся к ИВ, позволяют овладеть отдельными логическими правилами вывода для доказательства формул и построения выводов для различных формул.

ТЕМА 4. ИСЧИСЛЕНИЕ ВЫСКАЗЫВАНИЙ

Познавательные статьи:



Формы дистанционного обучения

Передача мяча двумя руками снизу

Значение правильной осанки для жизнедеятельности человека

Основные ошибки при выполнении передач мяча на месте