
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Правила вывода в исчислении предикатов.Содержание книги
Поиск на нашем сайте
Общезначимые формулы. Общезначимость аксиом ИП. Определение. Формула А называется общезначимой тогда и только тогда, когда она истинна в каждой интерпретации. Аксиомы ИП общезначимы.
Доказательство общезначимости доказуемых формул ИП.
Лемма о перестановочности универсальных кванторов.
Теорема о полноте ИП.
41. Системы одноместных предикатов формульных в арифметике. Определение 1. Одноместным предикатом Р(x) называется произвольная функция переменного x, определенная на множестве M и принимающая значение из множества {1; 0}. Множество М, на котором определен предикат Р(x), называется областью определения предиката Р(x). Множество всех элементов Р(х) – “х есть простое число” П(х) – “x=pa, где р-простое” Sq(x) – “х есть квадрат нат. числа” Сub(x) – “х есть куб нат. числа” Even(x) – “х есть четное число” Odd (x) – “х есть нечентное число” Even(x)~ ØOdd (x)
42. Система одноместных операций формульных в арифметике. Предикаты, так же, как высказывания, принимают значения И или Л, поэтому и к предикатам и к высказываниям применимы все операции логики высказываний. Одноместная операция это такая операция, где участвует только одно высказывание или предикат. Л огическое отрицание является одноместной операцией. Таблица истинности одноместной логической операции состоит из двух строк: два различных значения аргумента — «истина» (1) и «ложь» (0) и два соответствующих им значения функции. Логическая операция НЕ применяется к одному аргументу, в качестве которого может быть и простое, и сложное логическое выражение. Результатом операции НЕ является следующее: Результат операции отрицания истинен, когда исходное высказывание ложно, и наоборот. Приведем примеры отрицания: Высказывание «Земля вращается вокруг Солнца» истинно. Высказывание «Земля не вращается вокруг Солнца» ложно. 43. Система двухместных предикатов формульных в арифметике. Определение 1. Двухместным предикатом Р(x,y)называется функция двух переменных x и y, определенная на множестве М=М1хМ 2 и принимающая значения из множества {1;0}. В числе примеров двухместных предикатов можно назвать такие предикаты: Q(x, y) – “x=y” - предикат равенства, определенный на множестве RхR=R2; 44. Система двухместных операций формульных в арифметике. Предикаты, так же, как высказывания, принимают значения И или Л, поэтому и к предикатам и к высказываниям применимы все операции логики высказываний. Двухместная операция – операция в которой участвуют два высказывания или предиката. в таблице истинности двуместной логической операции — четыре строки: 4 различных сочетания значений аргументов — 00, 01, 10 и 11 и 4 соответствующих им значения функции. 45.Система двухместных операций формульных в арифметике. Двуместные операции z=lcm(x,y) наименьшее общее кратное z=gcd(x,y) наибольший общий делитель z=DIV(x,y) частное от деления x на y z=MOD(x,y) остаток от деления x на y z=exp(x,y) z=xy=eylnx p=gcd(x,y) ~ [(x|p&y|p)& A v(v|x&v|y)=>v|p] x=1 ~ A y [lcm(x,y)=y] x=1 ~ A y [gcd(x,y)=x] x=0 ~ A y [gcd(x,y)=y] 45.Определимость констант 0.1.2,… в системах не менее сильных чем следование. Neib(x,y) ~ [(x=s(y) v y=s(x)] SK(x)=y ~ S(S…(x)) /*K раз*/ =y x=0 ~ -E y(S(y)=x) x=1 ~ E y (S(y)=x & y=0) x=2 ~ E y (S(y)=x & y=1)
Предикаты взаимной простоты и делимости. Предикат ┴ - является двуместным и называется пр-м взаимной простоты Предикат | - является двуместным и называется пр-м делимости Определим ┴ в |: x┴y ~ A z (z|x & z|y => A p (z|p)) Определим | в *: x|y ~ E k [y=x*k] x=1 ~ A z [x┴z] x=0 ~ A y [y|x] x=1 ~ A y [x|y] x=0 ~ A z [x┴z] x┴y ó gcd(x,y)=1
Операция exp и определимость в ней сложения и умножения. Операция exp является двухместной операцией. exp(x,y)=z ~ z=xy (xy)z=xyz u=yz ó A x [exp(x,u)=exp(exp(x,y),z)] xy+z=xyxz u=y+z ó A x [exp(x,u)=exp(x,y)*exp(x,z)]
Теорема об неопределимости предикатов в алгебре с некоторыми отношениями выдерживающей некоторые автоморфизмы, но не являющиеся автоморфизмами предикатов.
Где FV – множество всех свободных переменных формулы А, а a1/v1 есть результат подстановки a1 вместо v1 в А.
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 522; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.87.151 (0.008 с.) |


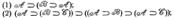










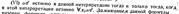








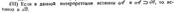

 , при которых предикат принимает значения “истина” (1), называется множеством (областью) истинности предиката Р(x), т.е. множество истинности предиката Р(х)- это множество
, при которых предикат принимает значения “истина” (1), называется множеством (областью) истинности предиката Р(x), т.е. множество истинности предиката Р(х)- это множество  . Так, например, предикат Р(x) – “x – простое число” определен на множестве N, а множество истинности IP для него есть множество всех простых чисел.
. Так, например, предикат Р(x) – “x – простое число” определен на множестве N, а множество истинности IP для него есть множество всех простых чисел.









