
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формула включений-исключенийСодержание книги
Поиск на нашем сайте
Теорема Эрдеша. Результат, доказанный Полом Эрдёшем и Дьёрдем (Джорджем) Секерешем таков: для данных r, s они показали, что любая последовательность длины по крайней мере (r -1)(s -1)+1 содержит или монотонно возрастающую подпоследовательность длины r, или монотонно убывающую длины s. Для r =3 и s =2, формула говорит, что любая переста новка трёх чисел имеет возрастающую подпоследовательность длиной три или убывающую подпоследовательность длиной два. Пример: Из шести перестановок чисел 1,2,3: -1,2,3 имеет возрастающую подпоследовательность длиной три -1,3,2 имеет убывающую подпоследовательность 3,2 -2,1,3 имеет убывающую подпоследовательность 2,1 -2,3,1 имеет две убывающие подпоследовательности, 2,1 и 3,1 -3,1,2 имеет две убывающие подпоследовательности, 3,1 and 3,2 -3,2,1 имеет три убывающие подпоследовательности длины 2, 3,2, 3,1, и 2,1. Теорема Эрдёша-Секереша может быть доказана несколькими разными способами; Майкл Стил дает обзор шести разных доказательств теоремы, в том числе с использованием принципа Дирихле и теоремы Дилворта.[2] Прочие способы доказательства, приводимые Стилом, включают оригинальное доказательство Эрдёша и Секереша и доказательство Блэквелла, Ловаса и самого Стила
Формула включений-исключений Формула включений-исключений (или принцип включений-исключений) —комбинаторная формула, позволяющая определить мощность объединения конечного числа конечных множеств, которые в общем случае могут пересекаться друг с другом. Например, в случае двух множеств
В сумме Таким же образом и в случае Впервые формулу включений-исключений опубликовал португальский математик Даниэль да Сильва в 1854 году. Но еще в 1713 году Николай Бернулли использовал этот метод для решения задачи Монмора, известной как задача о встречах, частным случаем которой является задача о беспорядках. Также формулу включений-исключений связывают с именами французского математика Абрахама де Муавра и английского математика Джозефа Сильвестра. В теории вероятностей аналог принципа включений-исключений известен как формула Пуанкаре.
5. Теорема о биекциях. Биекция — это отображение, которое является одновременно и сюръективным и инъективным. При биективном отображении каждому элементу одного множества соответствует ровно один элемент другого множества, при этом, определено обратное отображение, которое обладает тем же свойством. Поэтому биективное отображение называют ещё взаимно-однозначным отображением (соответствием), одно-однозначным отображением. Если между двумя множествами можно установить взаимно-однозначное соответствие (биекция), то такие множества называются равномощными. С точки зрения теории множеств, равномощные множества неразличимы. Взаимно-однозначное отображение конечного множества в себя называется перестановкой (элементов этого множества). Функция Переводит разные элементы множества X в разные элементы множества Y (инъективность). Иными словами,
Любой элемент из Y имеет свой прообраз (сюръективность). Иными словами,
Теорема о инъекциях. Отображение Формально это значит, что если два образа совпадают, то совпадают и прообразы ( Инъекцию можно также определить как отображение, для которого существует левое обратное, то есть
Теорема о сурьекциях. Отображение
Определение формулы АВ. 1)Простейшие высказ-я А,В,А1,А2..- формулы. 2)Если Φ,Ψ-формулы, то тогда (Φ), (Φ)→(Ψ), (Φ)&(Ψ), (Φ) v (Ψ), (Φ)↔(Ψ).3)Др формул нет. Все формулы АВ построены таким обр-м. Договоренность о снятии скобок: связки по старшинству: 1,2 v, &,3 →,↔.Поэтому в формуле (Φ) → Ψ, мы может убрать скобки и получить в итоге Φ → Ψ, исходя их старшинства связок.
Формулы АВ в юриспруденции.
У-убийство имело место после полуночи, С- Смит убийца,D-Джонс лжет, V-Джонс не встр ночью Смита. V→C v D C→(V Λ Y) Y→C v D C
(V→C v D) Λ [C→(V Λ Y)] Λ (Y→C v D) →C Попробуем подобрать значения С=л, V=и, Y=и, D=и. V,D,Y возможно. Возможно, что С не убийца. Вывод следователя был неполный. Он не учел все вещи. Эта формула бывает ложной. Т.е. с помощью математической логики мы пришли к заключению, что следователь не полностью исследовал все условия данного дела.
14.Полные системы логических связок. Определение. Множество функций алгебры логики называются полной системой, если любую функцию алгебры логики можно выразить формулой ------ Теорема: Система Ає{v, &, } – полна. Доказательство: Если функция алгебры логики f отличается от тождественного нуля, то А выражается в виде совершенной дизъюнктивной форме, в которую входит лишь дизъюнкция, конъюнкция, и отрицание. Если же f=0, то f есть x&x (ч.т.д). Лемма системы: 1.{x&y, x}2.{xVy, x}3.{x->y, x}4.{x|y} где x|y ~ (x&y) 5. {x Λ y} где |x Λ y| ~(xVy) полны Доказательство. 1.x&y= (xVy) 2.xVy= (x&y) 3.x->y= xVy= (x&y) А так как система Ає{v, &, } полна, то эти 3 пунка доказуемы. 4. x ~ x Λ x; xVy ~ (x Λ x) V (y Λ y) 5. x ~ x|x; xVy ~ (x|x) V (y|y) ч.т.д
Понятие вывода. Определение. Выводом из конечной совокупности формул H называется всякая конечная последовательность формул Свойства вывода: 1) Всякий начальный отрезок вывода из совокупности H есть вывод из H. 2) Если между двумя соседними членами вывода из H вставить некоторый вывод из H, то полученная новая последовательность формул будет выводом из H. 3) Всякий член вывода из совокупности H, является формулой, выводимой из H. Следствие. Всякий вывод из H является выводом его последней формулы. 4) Если 5) Для того, чтобы формула B была выводима из совокупности H, необходимо и достаточно, чтобы существовал вывод этой формулы из H.
Понятие вывода
ками вывода. Свойства:
23. Теорема о дедукции Лемма Кальмара
29. Теорема полноты исчисления высказывний.
Общезначимые формулы. Общезначимость аксиом ИП. Определение. Формула А называется общезначимой тогда и только тогда, когда она истинна в каждой интерпретации. Аксиомы ИП общезначимы.
Теорема о полноте ИП.
41. Системы одноместных предикатов формульных в арифметике. Определение 1. Одноместным предикатом Р(x) называется произвольная функция переменного x, определенная на множестве M и принимающая значение из множества {1; 0}. Множество М, на котором определен предикат Р(x), называется областью определения предиката Р(x). Множество всех элементов Р(х) – “х есть простое число” П(х) – “x=pa, где р-простое” Sq(x) – “х есть квадрат нат. числа” Сub(x) – “х есть куб нат. числа” Even(x) – “х есть четное число” Odd (x) – “х есть нечентное число” Even(x)~ ØOdd (x)
42. Система одноместных операций формульных в арифметике. Предикаты, так же, как высказывания, принимают значения И или Л, поэтому и к предикатам и к высказываниям применимы все операции логики высказываний. Одноместная операция это такая операция, где участвует только одно высказывание или предикат. Л огическое отрицание является одноместной операцией. Таблица истинности одноместной логической операции состоит из двух строк: два различных значения аргумента — «истина» (1) и «ложь» (0) и два соответствующих им значения функции. Логическая операция НЕ применяется к одному аргументу, в качестве которого может быть и простое, и сложное логическое выражение. Результатом операции НЕ является следующее: Результат операции отрицания истинен, когда исходное высказывание ложно, и наоборот. Приведем примеры отрицания: Высказывание «Земля вращается вокруг Солнца» истинно. Высказывание «Земля не вращается вокруг Солнца» ложно. 43. Система двухместных предикатов формульных в арифметике. Определение 1. Двухместным предикатом Р(x,y)называется функция двух переменных x и y, определенная на множестве М=М1хМ 2 и принимающая значения из множества {1;0}. В числе примеров двухместных предикатов можно назвать такие предикаты: Q(x, y) – “x=y” - предикат равенства, определенный на множестве RхR=R2; 44. Система двухместных операций формульных в арифметике. Предикаты, так же, как высказывания, принимают значения И или Л, поэтому и к предикатам и к высказываниям применимы все операции логики высказываний. Двухместная операция – операция в которой участвуют два высказывания или предиката. в таблице истинности двуместной логической операции — четыре строки: 4 различных сочетания значений аргументов — 00, 01, 10 и 11 и 4 соответствующих им значения функции. 45.Система двухместных операций формульных в арифметике. Двуместные операции z=lcm(x,y) наименьшее общее кратное z=gcd(x,y) наибольший общий делитель z=DIV(x,y) частное от деления x на y z=MOD(x,y) остаток от деления x на y z=exp(x,y) z=xy=eylnx p=gcd(x,y) ~ [(x|p&y|p)& A v(v|x&v|y)=>v|p] x=1 ~ A y [lcm(x,y)=y] x=1 ~ A y [gcd(x,y)=x] x=0 ~ A y [gcd(x,y)=y] 45.Определимость констант 0.1.2,… в системах не менее сильных чем следование. Neib(x,y) ~ [(x=s(y) v y=s(x)] SK(x)=y ~ S(S…(x)) /*K раз*/ =y x=0 ~ -E y(S(y)=x) x=1 ~ E y (S(y)=x & y=0) x=2 ~ E y (S(y)=x & y=1)
Теорема Эрдеша. Результат, доказанный Полом Эрдёшем и Дьёрдем (Джорджем) Секерешем таков: для данных r, s они показали, что любая последовательность длины по крайней мере (r -1)(s -1)+1 содержит или монотонно возрастающую подпоследовательность длины r, или монотонно убывающую длины s. Для r =3 и s =2, формула говорит, что любая переста новка трёх чисел имеет возрастающую подпоследовательность длиной три или убывающую подпоследовательность длиной два. Пример: Из шести перестановок чисел 1,2,3: -1,2,3 имеет возрастающую подпоследовательность длиной три -1,3,2 имеет убывающую подпоследовательность 3,2 -2,1,3 имеет убывающую подпоследовательность 2,1 -2,3,1 имеет две убывающие подпоследовательности, 2,1 и 3,1 -3,1,2 имеет две убывающие подпоследовательности, 3,1 and 3,2 -3,2,1 имеет три убывающие подпоследовательности длины 2, 3,2, 3,1, и 2,1. Теорема Эрдёша-Секереша может быть доказана несколькими разными способами; Майкл Стил дает обзор шести разных доказательств теоремы, в том числе с использованием принципа Дирихле и теоремы Дилворта.[2] Прочие способы доказательства, приводимые Стилом, включают оригинальное доказательство Эрдёша и Секереша и доказательство Блэквелла, Ловаса и самого Стила
Формула включений-исключений Формула включений-исключений (или принцип включений-исключений) —комбинаторная формула, позволяющая определить мощность объединения конечного числа конечных множеств, которые в общем случае могут пересекаться друг с другом. Например, в случае двух множеств
В сумме Таким же образом и в случае Впервые формулу включений-исключений опубликовал португальский математик Даниэль да Сильва в 1854 году. Но еще в 1713 году Николай Бернулли использовал этот метод для решения задачи Монмора, известной как задача о встречах, частным случаем которой является задача о беспорядках. Также формулу включений-исключений связывают с именами французского математика Абрахама де Муавра и английского математика Джозефа Сильвестра. В теории вероятностей аналог принципа включений-исключений известен как формула Пуанкаре.
5. Теорема о биекциях. Биекция — это отображение, которое является одновременно и сюръективным и инъективным. При биективном отображении каждому элементу одного множества соответствует ровно один элемент другого множества, при этом, определено обратное отображение, которое обладает тем же свойством. Поэтому биективное отображение называют ещё взаимно-однозначным отображением (соответствием), одно-однозначным отображением. Если между двумя множествами можно установить взаимно-однозначное соответствие (биекция), то такие множества называются равномощными. С точки зрения теории множеств, равномощные множества неразличимы. Взаимно-однозначное отображение конечного множества в себя называется перестановкой (элементов этого множества). Функция Переводит разные элементы множества X в разные элементы множества Y (инъективность). Иными словами,
Любой элемент из Y имеет свой прообраз (сюръективность). Иными словами,
Теорема о инъекциях. Отображение Формально это значит, что если два образа совпадают, то совпадают и прообразы ( Инъекцию можно также определить как отображение, для которого существует левое обратное, то есть
Теорема о сурьекциях. Отображение
Определение формулы АВ. 1)Простейшие высказ-я А,В,А1,А2..- формулы. 2)Если Φ,Ψ-формулы, то тогда (Φ), (Φ)→(Ψ), (Φ)&(Ψ), (Φ) v (Ψ), (Φ)↔(Ψ).3)Др формул нет. Все формулы АВ построены таким обр-м. Договоренность о снятии скобок: связки по старшинству: 1,2 v, &,3 →,↔.Поэтому в формуле (Φ) → Ψ, мы может убрать скобки и получить в итоге Φ → Ψ, исходя их старшинства связок.
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 952; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.007 с.) |

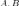 формула включений-исключений имеет вид:
формула включений-исключений имеет вид:
 элементы пересечения
элементы пересечения  учтены дважды, и чтобы компенсировать это мы вычитаем
учтены дважды, и чтобы компенсировать это мы вычитаем  из правой части формулы.
из правой части формулы. множеств процесс нахождения количества элементов объединения
множеств процесс нахождения количества элементов объединения  состоит во включении всего, затем исключении лишнего, затем включении ошибочно исключенного и так далее, то есть в попеременном включении и исключении. Отсюда и происходит название формулы.
состоит во включении всего, затем исключении лишнего, затем включении ошибочно исключенного и так далее, то есть в попеременном включении и исключении. Отсюда и происходит название формулы. называется биекцией (и обозначается
называется биекцией (и обозначается  ), если она:
), если она: .
. .
. называется инъекцией (или вложением, или отображением «в»), если разные элементы множества X переводятся в разные элементы множества Y.
называется инъекцией (или вложением, или отображением «в»), если разные элементы множества X переводятся в разные элементы множества Y.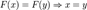 ). Инъективность является необходимым условием биективности (достаточно вместе ссюръективностью).
). Инъективность является необходимым условием биективности (достаточно вместе ссюръективностью). инъективно, если существует
инъективно, если существует  такое, что
такое, что  .
. называется сюръективным (или сюръекцией, или отображением на Y), если каждый элемент множества Y является образом хотя бы одного элемента множества X, то есть
называется сюръективным (или сюръекцией, или отображением на Y), если каждый элемент множества Y является образом хотя бы одного элемента множества X, то есть  . Для случая числовых функций это выражается как «функция, принимающая все возможные значения». Пример.
. Для случая числовых функций это выражается как «функция, принимающая все возможные значения». Пример.  — сюръективно.
— сюръективно.
 , всякий член которой удовлетворяет одному из следующих трех условий: 1) является одной из формул совокупности H; 2) является доказуемой формулой; 3) получается по правилу заключения из двух любых предшествующих членов последовательности
, всякий член которой удовлетворяет одному из следующих трех условий: 1) является одной из формул совокупности H; 2) является доказуемой формулой; 3) получается по правилу заключения из двух любых предшествующих членов последовательности  .
. , то всякий вывод из H является из W.
, то всякий вывод из H является из W.











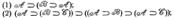



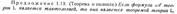







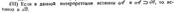

 , при которых предикат принимает значения “истина” (1), называется множеством (областью) истинности предиката Р(x), т.е. множество истинности предиката Р(х)- это множество
, при которых предикат принимает значения “истина” (1), называется множеством (областью) истинности предиката Р(x), т.е. множество истинности предиката Р(х)- это множество  . Так, например, предикат Р(x) – “x – простое число” определен на множестве N, а множество истинности IP для него есть множество всех простых чисел.
. Так, например, предикат Р(x) – “x – простое число” определен на множестве N, а множество истинности IP для него есть множество всех простых чисел.




