
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема 1: Теорема о следовании и импликацииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
(Здесь и далее символ Необходимость:
или
Достаточность: Значит
Обобщение теоремы 1: Г, Следствие:
Равносильность Равносильность формулы В формуле А будем обозначать: Формула А равносильна формуле В, если Основные формулы равносильности 1) 2) 3) 4) 5)Законы де Моргана
Для алгебры предикатов необходимо добавить закон коммутативности для кванторов
и законы де Моргана для кванторов
Отношение равносильности связано с отношением следования Теорема 2: Необходимость: или
Достаточность: в обратную сторону Теорема 3: связывает отношение равносильности с операцией эквивалентности
Следствие: Теорема 4: Теорема об эквивалентной замене Если
CB – формула, в которой все вхождения формулы А заменены на формулу В. Эта теорема позволяет изменять цепочки формул без изменения их истинностного значения. Пример
Булевы функции и нормальные формы
Логическими функциями называются функции от булевых переменных, значения которых - булево значение. Логическое выражение: Bn 2.1 Способы задания Задание логической функции с помощью таблицы Каждая логическая функция м.б. задана с помошью таблицы. Пример: Задана некая булева функция.
Всего 2n логических наборов переменных. Сколько м.б. различных булевых функций от n переменных? 2n-количество различных упоряд. наборов из n переменных. Логическая функция от n переменных м.б. задана как 2n различных наборов, при этом каждому набору должно соответсвовать одно из двух значений. Таким образом, при n=1, получаем 22=4 лог. Функций f(x).
При n=2,получаем 16 функций.
(x)– константа х (y)– константа y
Константа 0 1 – константа 1
| - штрих Шеффера
Задание логической функции с помощью формулы Логическую функцию можно задать с помощью формул и бинарных операций. Пример: У нас есть некая бинарная функция и.
Если вместо одной из переменных поставить любую бинарную функция, то получим функцию от 3-х переменных. Вывод:любая функция может быть задана как таблицей, так и формулой.
Унарные и бинарные операции Рассмотрим свойства унарных и бинарных операций: Коммутативность Коммутативными называют логические функции или логические операции, если они обладают следующим свойством: x # x = y # x, где # - &, v, ~, |, ↓, +
Ассоциативность
(x # y) # z = x # (y # z), где # - &, v, ~, +
Дистрибутивность x # (y Ъ z) = (x # y) Ъ (x # z), где #,Ъ - (&, v), (v,&),(&, +)
Обратные операции (x#y)=xЪy, где #,Ъ - (&,|), (v,↓), (>,→), (<,←), (~,+) Бинарное отрицание меняет логическую операцию на обратную.
Сведение к нескольким операциям
В частности все бинарные операции и логические функции могут быть сведены к трем операциям: Преобразования:
а) Все логические функции могут быть выражены через
б) через
в) через
г) можно выразить одной
д) через
Множество функций является полным, если можно выразить все другие функции через функции этого множества. Как определить какое множество функций является полным? Ответ на вопрос дает теорема Поста. Теорема Поста
Введем 5 различных классов функций: 1) F0 – функции сохраняющие «0».
При нулевых значениях аргумента, имеют значение- ноль.
2) F1 – функции сохраняющие «1».
В случае,когда все значения аргумента=1,значение фнкции=1.
3) F 2– монотонные функции.
n-местная логическая функция принадлежит классу монотонных функций, если у нас есть 2 набора Т.е. если набор увеличивается, значение функций также должно увеличиваться, поэтому функция монотонная.
4) F 3 – линейные функции.
где C0 ….Cn –являются булевыми константами (0 или 1).
5) F 4– самодвойственные функции. Двойственной функцией называется функция вида:
Самодвойственной функцией называется функция двойственная самой себе.
Теорема Поста. Есть множество функций. Множество функций является полным, если можно выразить все другие функции через функции этого множества. Для того, чтобы множество было полным, необходимо и достаточно, чтобы среди этого множества нашлась хотя бы одна функция, не сохраняющая 0, одна не сохраняющая 1, одна не монотонная, одна нелинейная функция и одна не самодвойственная. Нормальные формы
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 616; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.250.143 (0.008 с.) |


 будет соответствовать словесной формулировке «тогда и только тогда»)
будет соответствовать словесной формулировке «тогда и только тогда»)
 т.к.
т.к.  ,
,  ,
, 
 ,
, 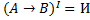
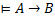



 Г
Г 


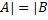
 в любой интерпретации I. В случае логики высказываний формулы равносильны, если их таблицы истинности одинаковы, что используется для доказательства равносильности.
в любой интерпретации I. В случае логики высказываний формулы равносильны, если их таблицы истинности одинаковы, что используется для доказательства равносильности. – идемпотентность
– идемпотентность ,
, 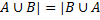 – коммутативность
– коммутативность – ассоциативность
– ассоциативность – дистрибутивность
– дистрибутивность





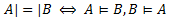







 B
B
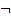 x
x
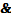

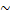





 x – отрицание х
x – отрицание х  - конъюнкция
- конъюнкция  – Дизъюнкция
– Дизъюнкция - Импликация
- Импликация  - эквивалентность
- эквивалентность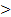 - сравнение x>y
- сравнение x>y 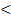 - сравнение x<y
- сравнение x<y - исключающее или
- исключающее или  - обратная импликация
- обратная импликация - стрелка Пирса
- стрелка Пирса

 .
.








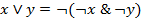







 :
:

 :
:

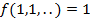




 , причем
, причем  , а это значит, что
, а это значит, что 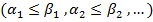 тогда значение
тогда значение  .
.






