
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Некоторые теоремы и формулы теории вероятностей.Содержание книги Поиск на нашем сайте
а) Операции над событиями (как подмножествами из W). Событие B состоящее из элементарных событий пространства W, не принадлежащих A, называется противоположным событию A. Обозначения противоположного события: `A, "не А ". Событие Суммой двух событий A и B называется событие, состоящее из элементарных событий, принадлежащих хотя бы одному из событий A или B. Сумму событий обозначают одним из символов A+B, " A или B ", A È B. Событие A+B происходит в результате опыта, если происходит либо A либо B либо оба вместе. Произведением двух событий A и B называется событие, состоящее из элементарных событий, принадлежащих одновременно и событию A и событию B. Наиболее употребительные обозначения произведения событий: A×B, " A и B ", A Ç B. Событие A B происходит в результате опыта, если происходят вместе оба события A и B. Понятие суммы и произведения легко обобщается на случай любого конечного числа событий. Например, для трех событий A+B+C=(A+B)+C, A×B×C=(A×B) C. Надо иметь в виду следующее: сумма A 1+ A 2 +…+An происходит в результате опыта, если происходит хотя бы одно из событий Ak (k =1, 2, …, n); произведение A 1· A 2· … · An происходит, если в результате опыта происходят все события A 1, A 2 ,… An. Разностью двух событий A и B называется событие A–B, состоящее из элементарных событий, принадлежащих A и не принадлежащих B. Возможные обозначения разности событий: A–B = A \ B. Здесь операция «\» означает теоретико-множественную разность (дополнение множества B в множестве А). В этом плане противоположное событие можно записать в виде Укажем основные свойства операций над событиями: 1. A+A=A, 2. A×A=A, 3. A+W=W, 4. A+Æ=A, 5. A×W=A, 6. A×Æ=Æ, 7. Ниже приведены простейшие свойства вероятности, вытекающие из определения и разобранных операций над событиями. Некоторые из них очевидны, другие формулируются в виде теорем, которые легко доказываются на основе классического определения вероятности. б) Теоремы сложения вероятностей. События A и B называются несовместными, если в их составе нет одних и тех же элементарных событий из W. В результате опыта несовместные события не могут произойти вместе. Несовместность означает, что A B = Æ. Таким же образом вводится понятие несовместности для большего числа событий: события A 1, A 2 ,..., Ak называются попарно несовместными, если любые два из них не могут произойти вместе, т. е. Ai Aj = Æ (i ¹ j, i =1, 2,..., k; j =1, 2,..., k). Теорема 1.1. Вероятность суммы конечного числа несовместных событий из одного и того же пространства W равна сумме вероятностей этих событий: P (A 1 +A 2 +...+Ak) = R (A 1)+ R (A 2)+...+ R (Ak). (1.4) На основании теоремы 1.1, доказанной для равновозможных исходов, можно обобщить определение вероятности события для случая, когда элементарные события пространства W не обязательно равновозможные. Для этого надо предположить, что вероятности P (w P (A) = Пусть событие А является частью события В, т. е. А Ì В. Можно сказать так же, что А влечет В. Тогда В = А+ (В–А), причем А и (В–А) несовместны. Из теоремы 1.1 Р (В) = Р (А) +Р (В–А) Þ P (В–А) = P (В) –P (А). Так как Р (В–А)³0, то Р (А)£ Р (В). Таким образом, если А влечет В, то Р (А)£ Р (В). (1.6) Будем говорить, что события A 1, A 2 ,..., Ak составляют полную группу, если в результате опыта обязательно происходит одно и только одно из этих событий. Из определения следует, что события, составляющие полную группу, попарно несовместны и их сумма равна достоверному событию W. На основании теоремы 1.1 сумма вероятностей событий, составляющих полную группу, равна 1, т.е. R(A 1 ) + R(A 2 ) +...+ R(Ak) =1. (1.7) События A и Рассмотрим случай, когда события A и B могут быть совместными. Для вероятности их суммы справедлива следующая Теорема 1.2. Вероятность суммы двух совместных событий равна сумме вероятностей этих событий минус вероятность их совместного появления. P (A+B) = P (A) + P (B) - P (A×B). (1.8) Теорему 1.2 можно обобщить на случай 3-х, 4-х и т.д. слагаемых. Однако получаемые при этом формулы очень громоздки и неудобны с точки зрения их практического применения. В связи с этим при отыскании вероятности суммы большого числа совместных событий удобнее перейти к противоположному событию. В результате получим формулу P (A 1+ A 2+...+ A k) = 1- P ( в) Условная вероятность. Теоремы умножения вероятностей. Очень часто вероятность события зависит от условий проведения эксперимента. Условной вероятностью события A при условии B (по-другому, при наличии B) называется вероятность события A вычисленная при условии, что событие B произошло. Условная вероятность обозначается символом P (A / B): P (A/B) = Меняя местами A и B, будем иметь P (B/A) = Выражая из этих соотношений P (A × B), приходим к теореме. Теорема 1.3. Вероятность произведения двух событий равна вероятности одного из них, помноженную на условную вероятность второго при наличии первого, т.е. P (A×B) = P (A) ×P (B/A) = P (B) ×P (A/B).(1.10) Формула (2.7) легко обобщается на случай 3-х сомножителей: P (A×B×C)= P ((A×B) ×C) = P (A×B) ×P (C /(A×B)) = P (A) ×P (B / A) ×P (C/ (A×B)). В общем случае P (A×B×C×...×D×E)= P (A) ×P (B / A) ×P (C/ (A×B)) ×...×P (E/ (A×B×C×... ×D)) (1.11) Событие A называется независимым от события B, если его вероятность не зависит от того, произошло событие B или нет, т. е. P (A/B) = P (A). В противном случае, если P (A/B) ¹ P (A), событие A зависит от B. Зависимость и независимость событий взаимны: если A зависит от B, то и B зависит от A. Действительно, если предположить, что A не зависит от B, то из (1.10) P (A) ×P (B/A) =P (B) P (A). Отсюда видно, что и P (B/A) = P (B). Таким образом, для двух независимых событий вероятность их произведения равна произведению вероятностей: P (A×B) = P (A) × P (B). (1.12) Иногда соотношение (1.10) используется для определения независимости событий, т. е. два события считаются независимыми, если вероятность их совместного появления равна произведению вероятностей. Отметим, что если А и В независимы, то независимы так же следующие пары событий: Множество событий A, B, C,..., D, E называется независимым в совокупности, если вероятность каждого из этих событий не зависит от того, происходили или не происходили любые другие события. Всякое множество, образованное из независимых в совокупности событий и противоположных к ним, будет независимо в совокупности. Для независимых в совокупности событий формула (1.11) принимает вид P (A×B×C×...×D×E) = P (A) ×P (B)×P (C) ...×P (D) ×P (E) (1.13) Пример 1.3. Для сигнализации об аварии установлены три независимо работающих сигнализатора, которые срабатывают при аварии с вероятностями 0.6, 0.7, 0.8. Найти вероятности следующих событий: A - при аварии сработали все три сигнализатора; B - при аварии сработал хотя бы один сигнализатор; C - при аварии сработали два сигнализатора. Решение. Введем события: A 1 - при аварии сработал 1-й сигнализатор, A 2 - 2-й, A 3 - 3-й. Тогда A = A 1 ×A 2 ×A 3, B = A 1 +A 2 +A 3, C= A 1 ×A 2 × Так как события A 1, A 2, A 3независимы между собой, то P(A)=P(A 1 ) ×P(A 2 ) ×P(A 3 )= 0.6×0.7×0.8=0.336, P(B)= 1 –P( г) Формула полной вероятности и формула Байеса. Рассмотрим следующую ситуацию. Некоторое событие A может произойти лишь совместно с одним из событий H 1, H 2 ,... Hk, составляющих полную группу. Считаются известными вероятности Р(Н 1 ). Р(Н 2 ),..., Р(Нk) и условные вероятности P(A/H 1 ), P(A/H 2 ),... P(A/Hk). Требуется найти вероятность события А. В этой ситуации событие А можно представить в виде суммы несовместных событий: А = H 1 ×A + H 2 ×A +¼+ Hk×A. По теоремам сложения и умножения вероятность события А определяется по формуле Р(А)=Р (H 1 )×Р(A/H 1 )+Р(H 2 )×P(A/H 2 )+¼+Р(Hk)×P(A/Hk), (1.14) которую называют формулой полной вероятности. Предположим теперь, что произведен опыт и в результате опыта произошло событие А. Поставим следующую задачу: с какой из гипотез вероятнее всего произошло событие А? Для ответа на поставленный вопрос следует найти вероятность каждой из гипотез Н 1, Н 2 ,..., Нk при условии, что событие А произошло, т. е. найти вероятности Р(Нi/А) (i= 1, 2, ...,k). С учетом формулы (1.10) Р(Нi)×Р(А/Нi) = Р(А)×Р(Нi/А). Отсюда получаем формулу Байеса
где Р(А) - вероятность события А, вычисляемая по формуле (1.14). Пример 1.4. В пирамиде 10 винтовок: 3 пристреленные и 7 не пристреленных. Вероятность поражения мишени из пристреленной винтовки равна 0.9, из непристреленной - 0.5. Стрелок поразил мишень из наудачу выбранной винтовки. Какая, вероятнее всего, была выбрана винтовка: пристреленная или не пристреленная? Для решения поставленной задачи введем гипотезы: Н 1 - выбрана пристреленная винтовка, Н 2 - выбрана не пристреленная винтовка и событие А - мишень поражена. По условию задачи Р(Н 1 ) = 3/10 = 0.3, Р(Н 2 ) = 7/10 = 0.7, Р(А/Н 1 ) = 0.9, Р(А/Н 2 ) = 0,5. Найдем сначала вероятность поражения мишени по формуле полной вероятности: Р(А) = 0.3×0.9+0.7×0.5 = 0.62. По формуле Байеса Р(Н 1 /А) =
|
||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 248; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.202.169 (0.008 с.) |

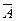
 происходит только в том случае, когда не происходит событие A и наоборот.
происходит только в том случае, когда не происходит событие A и наоборот.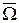 =Æ, 8.
=Æ, 8. 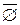 =W, 9. A+
=W, 9. A+ 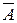 =W, 10. A×`A =Æ, 11. A+B=B+A – перестановочность слагаемых, 12. A×B=B×A – перестановочность сомножителей, 13. (A+B)+C=A+(B+C)=A+B+C – ассоциативность операции сложения, 14. (A×B) ×C = A× (B×C) = A×B×C – ассоциативность операции умножения, 15.
=W, 10. A×`A =Æ, 11. A+B=B+A – перестановочность слагаемых, 12. A×B=B×A – перестановочность сомножителей, 13. (A+B)+C=A+(B+C)=A+B+C – ассоциативность операции сложения, 14. (A×B) ×C = A× (B×C) = A×B×C – ассоциативность операции умножения, 15. 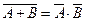 , 16.
, 16. 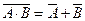 – законы дополнения, 17. A× (B+C) = (A×B) + (A×C), 18. A+ (B×C) = (A+B) × (A+C) – законы дистрибутивности.
– законы дополнения, 17. A× (B+C) = (A×B) + (A×C), 18. A+ (B×C) = (A+B) × (A+C) – законы дистрибутивности.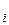 ) элементарных событий пространства W установлены (например, с помощью статистического определения). Так как элементарные события по предположению попарно несовместны, то вероятность произвольного события A Ì W можно определить следующей формулой:
) элементарных событий пространства W установлены (например, с помощью статистического определения). Так как элементарные события по предположению попарно несовместны, то вероятность произвольного события A Ì W можно определить следующей формулой: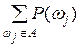 . (1.5)
. (1.5)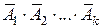 ). (1.9)
). (1.9)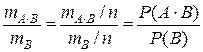 (P (B) ¹ 0).
(P (B) ¹ 0).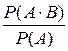 (P (A) ¹ 0).
(P (A) ¹ 0).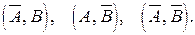
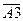 + A 1 ×
+ A 1 × 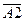 ×A 3 +
×A 3 + 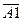 ×A 2 ×A 3. По условию P (A 1)=0.6, P (A 2) = 0.7 ,P (A 3) = 0.8,
×A 2 ×A 3. По условию P (A 1)=0.6, P (A 2) = 0.7 ,P (A 3) = 0.8, 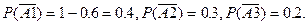
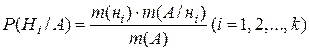 , (1.15)
, (1.15)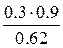 = 0.4355, Р(Н 2 /А) =
= 0.4355, Р(Н 2 /А) = 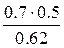 = 0.5645. Как видно, более вероятно, что была выбрана не пристреленная винтовка. Ä
= 0.5645. Как видно, более вероятно, что была выбрана не пристреленная винтовка. Ä


