
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Некоторые сведения из теории вероятностейСодержание книги Поиск на нашем сайте И МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ Тема 1. Основные понятия теории вероятностей.
Ниже будут применяться следующие сокращения: СВ – случайная величина; МО – математическое ожидание; СКВ – среднее квадратическое отклонение; ГС – генеральная совокупность; ДА – дисперсионный анализ; РА – регрессионный анализ. Символом Ä будет обозначаться конец решения или доказательства. 1.1. Случайные события и их вероятности. Повседневный опыт подсказывает, что большинство явлений окружающего нас мира случайны, непредсказуемы. С математической точки зрения, случайное явление – это такое явление, которое при неоднократном воспроизведении одного и того же опыта (испытания, эксперимента) протекает каждый раз несколько по-иному. Теорией вероятностей называют математическую науку, изучающую закономерности в случайных явлениях. Исходными для теории вероятностей являются понятия опыта и события. Под опытом (экспериментом, испытанием) понимается осуществление конкретного комплекса условий, при которых наблюдается то или другое явление, фиксируется тот или другой результат. В теории вероятностей рассматриваются опыты со случайным исходом. Дополнительно предполагается, что условия опыта можно воспроизводить многократно. Примерами опытов со случайным исходом могут быть: стрельба по мишени; подбрасывание игральной кости; физический опыт по измерению какой-либо величины; наблюдения за явлениями в природе или в обществе; акт выборки одного изделия из партии произведенных изделий, и т.д. Всякий мыслимый результат опыта называется элементарным событием и обозначается символом w. С каждым опытом связано некоторое множество элементарных событий. Введем следующее определение. а) Пространством элементарных событий называется множество элементарных событий, связанных с одним и тем же опытом, таких, что: 1) в результате опыта всегда происходит одно из элементарных событий; 2) все элементарные события взаимоисключающие друг друга, т.е. никакие два из них не могут произойти вместе. Пространство элементарных событий обозначается символом W. Если пространство W состоит из конечного или счетного числа элементарных событий, то его можно задавать перечислением: Очень часто опыт состоит в измерении некоторой величины X, которая может принять любое значение из интервала (a; b). В этом случае множество W состоит из несчетного количества элементарных событий. Его можно задать следующим образом: W={ x, x Î (a, b)}. б) Любое подмножество пространства элементарных событий будем называть событием и обозначать символами A, B, C, A Пустое множество Æ является подмножеством любого множества. Событие, соответствующее пустому множеству, называют невозможным событием и обозначают тем же символом Æ. Невозможное событие никогда не происходит в результате опыта. Аналогично, множество W также является подмножеством пространства элементарных событий. Событие, соответствующее W называют достоверным событием и обозначают тем же символом W. Достоверное событие всегда происходит в результате опыта. Все другие события в результате опыта либо происходят, либо не происходят. Их называют случайными событиями. Слово случайное в дальнейшем иногда будет опускаться, и случайные события будут называться просто событиями. Пример 1.1. Множеством всех событий для пространства W, состоящего из трех элементарных событий a, b, c, является F ={Æ, W, { a }, { b }, { c }, { a,b }, { a,c }, { b,c }}. в) Классическое определение вероятности. Рассмотрим пространство W, связанное с каким-либо опытом, состоящее из конечного числа n. элементарных событий. Дополнительно будем предполагать, что все элементарные события равновозможные. Это понятие интуитивное и не подлежит определению. Как правило, равновозможность является следствием симметрии предметов, участвующих в эксперименте. В искусственно организованных экспериментах дополнительно поддерживаются условия, обеспечивающие равновозможность появления любого из элементарных событий. Примеры опытов с равновозможными исходами: вытаскивание карты из колоды карт; выбор товара при покупке; заполнение карточки спортлото и др. Равновозможные элементарные события, образующие пространство W, называют исходами (случаями, шансами) данного опыта. Пусть A - некоторое событие из пространства W. Элементарные события, из которых составлено событие A, будем называть исходами, благоприятствующими событию A. Определение. Вероятностью события A называется число P(A), равное отношению числа исходов, благоприятствующих событию A, к числу всех возможных исходов данного опыта, т.е.
В формуле (1.1) знаменатель n - количество всех исходов рассматриваемого опыта, числитель mA - количество исходов, благоприятствующих событию A. Так как 0 £ mA £ n, то вероятность события - это число, заключенное в пределах от 0 до 1: 0£ R(A) £1, причем P (Æ)=0, P (W)=1. Для равновозможных элементарных событий Пример 1.2. Опыт: подбрасываются две игральные кости. Пусть событие A в этом опыте - сумма очков, выпавших на верхних гранях игральных костей ³ 10. Найти вероятность события A. Решение. Отметим, что исходы данного опыта можно задавать упорядоченными парами чисел (i; j), где i - количество выпавших очков на первой игральной кости, j - на второй. Так как i и j независимо пробегают множество чисел {1,2,...,6}, то количество исходов этого опыта n =6×6 = 36. Событию A (сумма выпавших очков ³ 10) благоприятствуют такие исходы: (4;6), (6;4), (5;5), (5;6), (6;5), (6;6), т.е. mA =6. Тогда P(A)= г) Геометрические вероятности. Если опыт сводится к выбору точки из множества, расположенного на прямой или на плоскости или в пространстве, то применяют геометрическое определение вероятности, которое является разновидностью классического определения вероятности. Множество, из которого выбирается точка, будем обозначать W и отождествлять его с пространством элементарных событий. Событиями в рассматриваемой ситуации будут подмножества из W - интервалы на прямой, геометрические фигуры на плоскости или в пространстве. При дополнительном предположении о равновозможности выбора любых точек из W, вероятности событий будут пропорциональны размерам соответствующих подмножеств. Пусть m(M) - мера множества M (длина, площадь, объем). Тогда формула (1.1) перепишется в виде P(A) = д) Статистическое определение вероятности. Не всегда опыт сводится к системе равновозможных исходов. В таких случаях прибегают к опытному или так называемому статистическому определению вероятности. Для пояснения рассмотрим опыт, при осуществлении которого появляется или не появляется интересующее нас событие A. Повторим опыт n раз. Пусть в m из них событие A произошло. Тогда отношение W=m/n называется относительной частотой появления события A в данной серии из n опытов. Произведем, далее, серию из n 1 опытов, в m 1 из которых появилось событие A. Получим новую относительную частоту W 1 =m 1 /n 1. Вообще говоря, W 1 отлична от W. Однако практикой установлено, что с увеличением числа опытов относительные частоты стабилизируются и начинают колебаться около вероятности события A. В связи с этим за вероятность события A приближенно можно принять его относительную частоту при большом n: P(A) @ В этом и состоит суть статистического определения вероятности. В формуле (1.3) n - количество проведенных опытов (достаточно большое число), m - количество опытов, в которых появилось событие A. Имеется много примеров, когда вероятности событий определяются только статистически: вероятность рождения мальчика (для многих стран эта вероятность равна 0.516); только статистически можно установить вероятность брака при производстве однотипной продукции на предприятии и другие.
|
||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 298; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

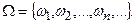
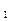 , B
, B 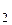 и т.д. Событие A происходит (появляется) в результате опыта, если происходит одно из элементарных событий, принадлежащих A. Будем говорить, что событие A влечет событие B, если A является частью подмножества B. При этом пишут A Ì B. События A и B называются эквивалентными, если A Ì B и B Ì A.
и т.д. Событие A происходит (появляется) в результате опыта, если происходит одно из элементарных событий, принадлежащих A. Будем говорить, что событие A влечет событие B, если A является частью подмножества B. При этом пишут A Ì B. События A и B называются эквивалентными, если A Ì B и B Ì A.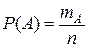 . (1.1)
. (1.1)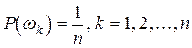 .
.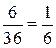 Ä
Ä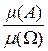 . (1.2)
. (1.2)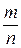 . (1.3)
. (1.3)


