
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Повторные испытания. Формула Бернулли.Содержание книги Поиск на нашем сайте
а) На практике часто приходится встречаться с задачами, в которых один и тот же опыт повторяется многократно. В каждом из этих опытов наблюдается одно и то же событие А. Совокупность опытов (испытаний) называют независимой, если вероятность появления события А в i -м опыте не зависит от исходов предыдущих испытаний. Рассматриваемые ниже совокупности опытов будут предполагаться независимыми. Примером такой ситуации может быть производство однотипных деталей станком-автоматом, который работает в одних и тех же условиях. Однако некоторые из производимых деталей удовлетворяют стандарту (событие А), другие нет. Введем обозначения: p = P (A) - вероятность появления события А в каждом отдельно взятом опыте; q = 1– p - вероятность не появления. Дополнительно предполагается, что 0 < p < 0. Поставим следующую задачу: найти вероятность события Вk, состоящего в том, что в n независимых опытах событие А появится ровно k раз. Обозначим эту вероятность через Pn (k) = Р (Вk). Событие Вk происходит, если в каких то k опытах из n событие А появляется, а в остальных n–k опытах не появляется. Пусть события Аi (i= 1, 2, ...,n), означают тот факт, что А появилось в i -м по счету опыте. Тогда один из вариантов появления события Вk можно задать в виде А 1 ×А 2 ×...×Аk ×
б) Рассмотрим, как распределяются в зависимости от k вероятности, вычисляемые по формуле (1.16). С помощью этой формулы находим, что отношение При больших n формула Бернулли приводит к громоздким вычислениям. Приведем формулировку трех теорем, упрощающих эти вычисления. в) Локальная теорема Муавра – Лапласа. Пусть вероятность наступления некоторого события А в n независимых опытах постоянна и равна p (0< p <1), q = 1– p – вероятность не появления события А в одном опыте. Обозначим
Тогда вероятность Pn (k) того, что событие А наступит ровно k раз в этих опытах удовлетворяет при n ®¥ соотношению
Из локальной теоремы Муавра – Лапласа вытекает следующая приближенная формула. При больших n Pn (k) @ Обычно эта формула применяется при n> 30 и n×p×q ³ 9. Значения функции j (x) можно найти по таблице для x Î[0; 4] (см. приложение 1). При x >4 j (x) @0. При x <0, j (x) = j (-x). г) Интегральная теорема Муавра – Лапласа. Пусть k есть число наступлений события А в n независимых опытах, в каждом из которых эта вероятность постоянна и равна p (0< p <1). Тогда имеет место соотношение
Если выбрать
Тогда при больших n (n> 30, n×p×q ³ 9) вероятность Pn (k 1 £ k£ k 2) приближенно можно найти по формуле
где x 1= Интеграл, определяющий функцию F (x), «не берущийся». Значения F (x)можно найти по таблице для x Î[0; 4] (см. приложение 2). При x > 4 F (x) @ 0.5. Так как функция F (x)нечетная, то для x < 0 F (x) = –F (– x). в) Большой круг задач связан с вычислением вероятностей Pn (k) при малых р (случай редко появляющихся событий). В этих случаях формула (1.17) дает существенные погрешности. Основу для вычисления вероятностей Pn (k) при больших n и малых p дает нижеследующая теорема. Теорема Пуассона. Пусть вероятность события А при каждом опыте в серии из n независимых опытов равна a / n, где a >0 – постоянная, не зависящая от n. Тогда
г) Приведем некоторые следствия из интегральной теоремы Муавра – Лапласа. Предварительно рассмотрим вероятность неравенства
где e – положительная постоянная,
Формула (1.21) устанавливает вероятность того, что в n независимых опытах (при больших n) относительная частота появления события А отклонится от вероятности появления А в одном опыте на величину, меньшую e. С увеличением n эта вероятность стремится к единице.
Простейший поток событий а) Рассмотрим одну ситуацию, где встречается формула (1.19). Введем определение: потоком событий называется последовательность однородных событий, появляющихся в случайные моменты времени. Примеры потоков: приход кораблей в порт, поступление вызовов на станцию скорой помощи, приходы посетителей в магазин и др. Одна из задач, связанных с потоками событий, состоит в определении вероятности P ( t 1, t 2)(k) (1.22) того, что на интервале времени (t 1, t 2) произойдет ровно k событий потока. Отметим следующие свойства потоков. а1) Стационарность. Это свойство означает, что вероятность (1.22) не зависит от начального момента времени t 1, а зависит лишь от длины интервала t = t 2– t 1, т. е. формула (1.22) принимает вид Pt (k). Из этого следует, что среднее число событий, появляющихся в единицу времени, постоянно. Обозначим его l и будем называть интенсивностью потока. а2) Ординарность. Это свойство означает, что за бесконечно малый промежуток времени dt произойдет не более одного события потока. Точнее, вероятность попадания на малый промежуток времени dt двух и более событий Pdt (k) (k =2, 3,...) ничтожно мала по сравнению с Pdt (1). а3) Отсутствие последействия, т. е. вероятность попадания того или другого числа событий на заданный участок оси 0 t не зависит от того, сколько событий попало на любой другой не пересекающийся с ним участок. В частности, «будущее потока не зависит от его прошлого». Поток событий, обладающий указанными тремя свойствами – стационарностью ординарностью и отсутствием последействия, называется простейшим (или стационарным пуассоновским) потоком. Можно доказать, что вероятность Pt (k) того, что за время t произойдет ровно k событий простейшего потока определяется формулой
где l – интенсивность потока (среднее число событий, появляющихся в единицу времени),. k = 0, 1, 2,.... Пример 1.5. На АТС поступает простейший поток событий с интенсивностью 0.2 (вызов/мин). Найти вероятность того, что за пять минут: а) не придет ни одного вызова; б) придет ровно один вызов; в) придет хотя бы один вызов. Решение. По условию l=0.2, t =5, l t =1. Тогда а) в) P 5(k ³1) = 1 – P 5(0) = 1–0.36788=0.73212. Ä
Тема 2.. Случа й ные величины (СВ).
Одномерные дискретные СВ. а). Основные определения. Очень часто в результате эксперимента появляется численное значение, причем заранее (до опыта) нельзя точно предсказать, какое именно значение появится. Математические модели таких экспериментов называются случайными величинами (сокращенно СВ). Примеры СВ: число вызовов, поступивших на станцию скорой помощи в течение суток; величина отклонения точки приземления снаряда от центра цели и др. В одних экспериментах измеряют одну какую то величину - такими экспериментами определяются одномерные СВ; в других экспериментах сразу измеряют несколько величин, образующих комплекс - случайные величины в таких экспериментах называют многомерными (векторными) СВ или системами СВ. Обозначения: X, Y, Z,... - одномерные СВ; (U,V) - двумерная СВ; (X( 1 ) , X( 2 ) ,..., X(n)) - n -мерная СВ. Одномерные СВ, из которых составлена система, называют ее компонентами. При задании многомерной СВ компоненты должны быть упорядочены. Пример 2.1. Станок изготавливает детали цилиндрической формы. Контролируются следующие размеры детали: L – длина детали; D – ее диаметр; M – масса. СВ (L, D, M) является трехмерной. По множеству принимаемых значений одномерные СВ делятся на дискретные и непрерывные. СВ называется дискретной, если множество ее значений конечное или счетное, и непрерывной - если множество значений заполняет некоторый интервал действительных чисел. Обозначения: W X = { x 1, x 2 ,...,xn,... } - множество значений одномерной дискретной СВ X; W Y = { y, y Î [ a, b ]} - множество значений одномерной непрерывной СВ Y. Законом распределения СВ называется любое правило, позволяющее находить вероятности всевозможных событий, связанных со случайной величиной (например, что она примет какое-то значение или значение из некоторого интервала). Наиболее простую форму можно придать закону распределения дискретной одномерной СВ. Для этого достаточно задать множество ее возможных значений и указать, как часто они появляются в результатах экспериментов, т. е указать вероятности, с которыми эти значения принимаются. Дополнительное предположение: в результате опыта СВ принимает одно и только одно из своих значений. Из этого следует, что сумма вероятностей всех значений равна единице. Эта единица как-то распределяется между значениями СВ (отсюда и термин «распределение»). Дискретную одномерную СВ можно задать таблицей (рядом распределения): Таблица 2.1
В верхней строке таблицы перечисляются в порядке возрастания все возможные значения дискретной СВ, в нижней – вероятности этих значений. Пусть некоторая функция j(x) определена для всех значений дискретной СВ Х. Тогда можно определить функцию Y =j(Х), которая является СВ и задается следующей таблицей: Таблица 2.2
Таблицу 2.2 нельзя считать законом распределения СВ j(Х). Для его получения значения j(хi) в верхней строке следует упорядочить по возрастанию и одинаковые из этих значений записать как одно значение, предварительно сложив соответствующие им вероятности. Обычно случайные величины называют распределениями. б) Числовые характеристики дискретных одномерных СВ. Математическим ожиданием дискретной СВ Х называется сумма произведений всех ее значений на соответствующие вероятности. Математическое ожидание будем обозначать одним из символов М (Х) или mx. Предполагая, что дискретная СВ задана таблицей 2.1, запишем математическое ожидание в виде формулы
Так как математическое ожидание СВ и среднее значение измеряемой величины определяются однотипными формулами, то М (Х) называют центром распределения или средним значением СВ. Центрированной называют СВ Еще одной из характеристик положения является мода. Модой Mo = Мо(Х) дискретной СВ Х называют значение СВ Х, имеющее наибольшую вероятность. Дискретная СВ может иметь несколько мод. Для характеристики разбросанности (рассеивания) значений СВ относительно центра распределения, вводятся понятия дисперсии и среднего квадратического отклонения. Дисперсией
Слово «дисперсия» означает «рассеивание». Отметим, что дисперсия имеет размерность квадрата СВ, что не всегда удобно. Для наглядности в качестве характеристики рассеивания удобнее пользоваться числом, размерность которого совпадает с размерностью СВ. Для этого из дисперсии извлекают квадратный корень и вводят следующее определение. Средним квадратическим отклонением (сокращенно СКО) или стандартом СВ Х называется квадратный корень из дисперсии:
Безразмерную величину
называют коэффициентом вариации. Начальные
На практике эти формулы используются при j = 1, 2, 3, 4. Легко видно, что n 1= M (X), m 1=0, m 2= D (X). С помощью центральных моментов m 3 и m 4 определяются безразмерные коэффициенты асимметрии As и эксцесса ex: As = m 3 /sx 3, ex = (m 4 /sx4) - 3. (2.6)
Одномерные непрерывные СВ. Так как множество значений непрерывной СВ не является счетным, то задать распределение вероятностей непрерывной СВ в виде таблицы невозможно. Необходимы другие способы задания случайных величин. Введем понятие функции распределения, пригодное для задания как дискретных, так и непрерывных СВ. а) Функцией распределения одномерной случайной величины X называется функция F(x) действительного переменного x Î R (R - множество действительных чисел), равная вероятности выполнения неравенства X<x, т. е.: F (x) = P (X < x) = P (X Î (-¥, x)), (2.7) В формуле (2.7) Х - символ случайной величины, х - аргумент функции распределения. Его можно обозначать любой другой буквой. Если в рассмотрениях одновременно участвуют СВ Х, Y,..., то их функции распределения можно обозначать FX (x), FY (у),..., или F 1(x), F 2(у),.... Приведем основные свойства функции F (x), вытекающие из ее определения. а1) Очевидно 0 £ F (x) £1, F (-¥)=0, F (+¥) =1. а2) F (x) неубывающая функция, т. е. если x 1 < x 2, то F (x 1) £ F (x 2 а3) Вероятность попадания СВ в интервал P (a £ X < b) = F (b) –F (a), (2.8) а4) Если множеством значений СВ X является конечный интервал (a, b) или отрезок [ a, b ], то функция распределения такой СВ имеет вид
где F 0(x) – неубывающая функция, причем F 0(a) = 0, F 0(b) = 1. б) Плотностью вероятности одномерной непрерывной СВ X в точке х называется следующий предел (если он существует):
Таким образом, плотность вероятности является производной от функции распределения. Чтобы формула (2.9) имела смысл, вводится дополнительное предположение, что функция распределения непрерывной СВ непрерывна на всей числовой оси и дифференцируема (за исключением, быть может, конечного числа точек). Выпишем свойства плотности вероятности, вытекающие из формулы (2.9). б1) Так как функция распределения не убывающая, то плотность вероятности не отрицательна, т. е. р (х) ³ 0. б2) Так как функция распределения F (x) является одной из первообразных для p (х), то
т. е. вероятность попадания непрерывной СВ в интервал, равна интегралу от плотности вероятности по этому интервалу. Полагая в (2.10) a =–¥, b=+¥, получим соотношение
б3) Если в (2.10) положить a =–¥, b=х, получаем выражение функции распределения через плотность вероятности:
б) Если значения непрерывной СВ X лежат в интервале (a; b), то p (х)=0, при x<a или x>b. б5) При малых Dx вероятность P (x £ X < x+Dx) @p (x) ×Dx, x Î[ x,x+Dx ]. Таким образом, непрерывную СВ можно задать либо функцией распределения, либо плотностью вероятности. В качестве функции распределения может служить любая непрерывная неубывающая функция F (x), удовлетворяющая условиям 0 £ F (x) £ 1, F (-¥) = 0, F (+¥) = 1. В качестве плотности вероятности можно взять любую неотрицательную кусочно-непрерывную функцию, удовлетворяющую условию (2.11). в) Числовые характеристики непрерывных одномерных СВ определяются формулами
Отметим, что
Другие числовые характеристики
Модой непрерывной СВ называется точка глобального максимума плотности вероятности. Для непрерывной СВ вводится понятие медианы Me = Me (X), которая определяется из соотношения: P (X £ Me) = P (X ³ Me)=0.5, т. е. медиана делит множество значений СВ Х на две части, вероятности попадания в которые одинаковы и равны 0.5.
Двумерные СВ. а) Двумерные дискретные СВ. Многомерными СВ называются векторы, координаты (компоненты) которых являются одномерными СВ. По–другому, многомерные СВ называются векторными СВ или системами СВ. В данном пособии будут рассматриваться, в основном, двумерные СВ. Двумерные дискретные СВ (X; Y) задаются таблицами с двумя входами. 1-й столбец содержит значения СВ Х: WX = { x 1, x 2 ,..., xm }; 1-я строка содержит значения СВ Y: WY = { y 1, y 2,, ..., yn }. На пересечениях строк и столбцов стоят вероятности, с которыми каждая пара значений принимается: pi,j = P(X=xi, Y=yj) (таблица 2.3):
Таблица 2.3
Таблицу 2.3 называют так же матрицей распределения вероятностей двумерной СВ. Сумма вероятностей pi,j по всем клеткам таблицы 2.3 должна равняться единице. 1-я задача, связанная с двумерными СВ - найти законы распределения компонент X и Y. Для ее решения отметим, что событие (X=xi) = (Y=y 1, X=xi) + (Y=y 2, X=xi) +…+ (Y=yn, X=xi). Отсюда следует, что P(X=xi) = pi ,1 + pi, 2 +...+ pi,n. Аналогичное соотношение можно записать и для вероятности P(Y=yj). В таблице 2.3 введены дополнительная строка и дополнительный столбец, дающие распределение вероятностей составляющих X и Y двумерной СВ (X,Y). Таким образом, 1-й и последний столбцы таблицы 2.3 дают закон распределения СВ X, 1-я и последняя строки дают закон распределения СВ Y. Выражения p·,j и pi, · означают суммирование:
2-я задача связана с зависимостью и независимостью компонент. Введем определение: компоненты X и Y двумерной дискретной СВ (X,Y) называются независимыми между собой, если для всех индексов i, j выполнено условие P (X=xi, Y=yj) = P (X = xi) × P (Y=yj). Из определения независимости следует, что для независимых СВ Многомерная СВ (X (1) ,X (2) ,...,X ( k )) задается в виде таблицы:
где
б) Двумерные непрерывные СВ. Функцией распределения двумерной СВ называется функция двух переменных F (x,y), равная вероятности того, что одновременно СВ X принимает значение, меньшее x, а СВ Y – значение, меньшее y: F (x,y) =P (X<x; Y<y) =P (XÎ (-¥, x) ;YÎ (-¥, y)). (2.14) Графически P (X<x;Y<y) означает вероятность попадания случайной точки (X,Y) в бесконечный прямой угол с вершиной в точке (x,y) (рис. 2.1).
Из определения вытекают следующие свойства F(x,y): F1) 0 £ F(x,y) £ 1, F (- ¥, y)= F (x, - ¥) = 0, F (+ ¥,+ ¥) =1; F2) F(x,y) - неубывающая функция по каждой переменной; F3) вероятность попадания двумерной СВ в прямоугольник (рис. 2.2) определяется формулой P(a £ X < b, c £ Y < d) = F(b,d) - F(b,c) - F(a,d) + F(a,c); F4) функции распределения компонент X и Y двумерной СВ (X, Y) (маргинальные функции распределения) находятся по формулам FX(x)=P(X<x)= F(x,+ ¥), FY(y)= P(Y<y)= F(+ ¥, y) F5) Компоненты X и Y двумерной СВ называются независимыми, если P(X<x;Y<y)=P(X<x)×P(Y<y). Из определения следует, что для независимых СВ функция распределения представляется в виде произведения двух функций, одна из которых зависит только от x а другая только от y: F (x, y) = FX(x)×FY(y). Плотностью вероятности (плотностью распределения) двумерной непрерывной СВ (X,Y) в точке (x, y) называется предел средней плотности распределения вероятностей в прямоугольнике (x £ X < x + Dx, y£ Y < y + Dy) при условии, что Dx ® 0 и Dy ® 0 (при условии дважды дифференцируемости F (x, y) этот предел существует). Выведем выражение для плотности вероятности через функцию распределения. По определению
Вычисляя пределы, получаем, что плотность вероятности является смешанной производной второго порядка от функции распределения:
Выпишем основные свойства плотности вероятности. P1) p(x, y) ³ 0; P2) вероятность попадания двумерной СВ (X, Y) в область G определяется формулой P((X, Y) Î G) = P3) выражение функции распределения через плотность вероятности имеет вид
P4) при x = +¥, y = +¥
Обычно это свойство называют условием нормировки. P5) если известна совместная плотность распределения p(x, y) двумерной СВ (X, Y), то плотности распределения компонент получаются интегрированием p(x, y):
P6) Если компоненты X и Y двумерной СВ независимы, то плотность распределения представляется в виде произведения двух функций:
в). Числовые характеристики многомерных (двумерных) СВ. Числовые характеристики двумерных СВ, такие как математическое ожидание, дисперсия, среднее квадратическое отклонение, мода, медиана, коэффициенты асимметрии и эксцесса определяются как векторы, составленные из соответствующих числовых характеристик компонент, т. е. M(X, Y) = (mx, my), D(X, Y) =(Dx, Dy) и т. д.. Поэтому рассмотрим лишь числовые характеристики, устанавливающие связи между компонентами. К ним относятся совместные начальные и центральные моменты. Формулы приводятся для дискретных СВ а в скобках - для непрерывных СВ. Из них получаются выражения для математического ожидания, дисперсии и других характеристик компонент. Предполагается, что дискретная СВ задана таблицей 2.3 Начальные
Особую роль играет центральный момент порядка 1+1. Его называют корреляционным моментом или ковариацией и обозначают одним из символов
Отношение
которое является безразмерной величиной, называется линейным коэффициентом корреляции между СВ X и Y.
Тема 3. Примеры распределений СВ.
Для приводимых ниже СВ указаны ряды распределения (в случае дискретных СВ), плотность вероятности с функцией распределения (в случае непрерывных СВ), а так же значения числовых характеристик. 3.1. Биномиальное распределение. Пусть вероятность наступления некоторого события А в каждом из n независимых опытов постоянна и равна p (0< p <1), q =1– p – вероятность не появления события А. Введем СВ Х – число наступлений события А в n независимых опытах. Найдем закон распределения и числовые характеристики СВ Х. Очевидно, что множество значений СВ Х WX={0, 1, 2,..., k,..., n }. Вероятности, с которыми принимаются значения СВ Х, определяются по формуле Бернулли:
Таким образом, СВ Х полностью определена. Отметим, что вероятности
Числовые характеристики:
Модой биномиального распределения является число k 0– наивероятнейшее число наступлений события А в n независимых испытаниях. Если n×p–q не является целым числом, то k 0 – целое число, заключенное между n×p–q и n×p+p. В частном случае, когда n×p–q является целым числом, биномиальное распределение имеет две моды n×p–q и n×p+p. Коэффициенты асимметрии и эксцесса
3.2. Распределение Пуассона. СВ Х имеет распределение Пуассона, если ее возможные значения составляют целые неотрицательные числа 0, 1, 2,..., k,..., а соответствующие вероятности выражаются формулой
Числовые характеристики распределения Пуассона:
Если параметр a является целым числом, то распределение Пуассона имеет две моды a –1 и a. В противном случае Мо есть целое число из промежутка (a –1, a). Равномерное распределение. Будем говорить, что СВ Х имеет равномерное распределение на отрезке [ a, b ] (подчиняется закону R [ a, b ]), если ее плотность вероятности определяется формулой
т. е. равна ненулевой константе на [ a, b ] и нулю вне [ a, b ]. Числовые характеристики:
Равномерное распределение моды не имеет. 3.4. Показательное (экспоненциальное) распределение. Функция распределения и плотность вероятности показательного распределения:
Числовые характеристики:
3.5. Нормальное распределение. СВ X называется нормальным распределением, если множество ее значений совпадает с множеством действительных чисел, а плотность вероятности определяется формулой
Параметру a можно придавать любое действительное значение, параметр s>0. На рис. 3.1 изображен график функции (3.1) при значениях параметров a = 4, s = 1.
Рис. 3.1 При доказательстве многих предложений, связанных с нормальным распределением, используется интеграл Эйлера - Пуассона
Так как
то основное соотношение для (3.1) выполнено Найдем числовые характеристики нормального распределения.
Последний интеграл равен нулю, как интеграл от нечетной функции по симметричному промежутку. Аналогично
С помощью той же замены
Таким образом, найдены основные числовые характеристики нормального распределения:
Точно так же можно показать, что Легко видеть, что функция (3.1) достигает максимума при x=a. Отсюда следует, что Функцию распределения нормального закона можно представить в виде
где F (x) (функция Лапласа, интеграл вероятностей), определяется выражением:
Значения функции Ф(х) можно найти по таблице (приложение 2). Замечание 1.1. Нормальное распределение с параметрами a и s обозначают для краткости символом N (a, s). Вероятность попадания нормально распределенной СВ X в интервал (a, b) определяется формулой
Из (3.3)
При d =3× s из (3.4) получаем, так называемое, правило трех сигм:
т. е. значения нормально распределенной СВ практически не выходят за пределы интервала (а –3× s, а +3× s). Ниже приведены основные (универсальные) распределения, применяемые при проверке статистических гипотез. 3.6. Распределение хи-квадрат( Пусть X 1, X 2 ,...,Xn - независимые в совокупности случайные величины, имеющие нормальное распределение N (0, 1). Сумму квадратов этих СВ называют распределением хи-квадрат с n степенями свободы. Обозначение
Для СВ
где постоянная An выбирается из условия нормировки, т. е.
График плотности распределения хи–квадрат при n=4 изображен на рис. 3.2.
Рис. 3.2 Числовые характеристики распределения хи–квадрат с n степенями свободы: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |

 . Другие варианты появления события Вk отличаются местами, на которых стоят сомножители Аi, например,
. Другие варианты появления события Вk отличаются местами, на которых стоят сомножители Аi, например,  и т. д. Количество таких вариантов равно числу сочетаний из n элементов по k элементов, т. е. равно
и т. д. Количество таких вариантов равно числу сочетаний из n элементов по k элементов, т. е. равно  , причем любые два варианта несовместны между собой. В связи с независимостью опытов, вероятность одного осуществления события В всегда равна
, причем любые два варианта несовместны между собой. В связи с независимостью опытов, вероятность одного осуществления события В всегда равна  . Приведенные рассуждения позволяют записать выражение вероятности Рn (k) в виде формулы, которую называют формулой Бернулли:
. Приведенные рассуждения позволяют записать выражение вероятности Рn (k) в виде формулы, которую называют формулой Бернулли: . (1.16)
. (1.16) . Если
. Если  Û k <n×p–q, то Рn (k+ 1 ) > Pn (k), т. е. вероятности Pn(k) возрастают с увеличением k. Если же k>n×p – q, то вероятности Pn (k) уменьшаются с увеличением k. Из этих соотношений видно, что между n×p–q и n×p–q+ 1 = n×p+p существует целое число k 0, для которого вероятность Pn (k 0) имеет наибольшее значение. Число k 0называется наивероятнейшим числом наступлений события А в независимых испытаниях. В частном случае, когда n×p–q является целым числом, Pn (n×p–q) = Pn (n×p+p), т. е. существует два наивероятнейших числа.
Û k <n×p–q, то Рn (k+ 1 ) > Pn (k), т. е. вероятности Pn(k) возрастают с увеличением k. Если же k>n×p – q, то вероятности Pn (k) уменьшаются с увеличением k. Из этих соотношений видно, что между n×p–q и n×p–q+ 1 = n×p+p существует целое число k 0, для которого вероятность Pn (k 0) имеет наибольшее значение. Число k 0называется наивероятнейшим числом наступлений события А в независимых испытаниях. В частном случае, когда n×p–q является целым числом, Pn (n×p–q) = Pn (n×p+p), т. е. существует два наивероятнейших числа.

 ,
,  ,
,  , k = 0, 1 ,...,n. (1.17)
, k = 0, 1 ,...,n. (1.17)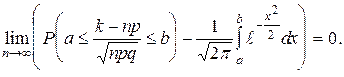
 то
то  .
. , (1.18)
, (1.18) , x 2=
, x 2=  ,
,  .
. . Следствие из теоремы Пуассона. При больших n и малых p (обычно p < 0,1, n×p×q <9)
. Следствие из теоремы Пуассона. При больших n и малых p (обычно p < 0,1, n×p×q <9)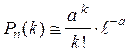 , где a = n×p, k = 0, 1, ...,n. (1.19)
, где a = n×p, k = 0, 1, ...,n. (1.19) , (1.20)
, (1.20) – относительная частота появления некоторого события А в n независимых опытах. Остальные величины в (1.20) имеют тот же смысл, что и в п. а). По интегральной теореме Муавра – Лапласа
– относительная частота появления некоторого события А в n независимых опытах. Остальные величины в (1.20) имеют тот же смысл, что и в п. а). По интегральной теореме Муавра – Лапласа (1.21)
(1.21) (1.23)
(1.23) б)
б) 

 . (2.1)
. (2.1) , множество значений которой (см. таблицу 2.2) { x 1 -mx, x 2 -mx,..., xn-mx,...}, а вероятности
, множество значений которой (см. таблицу 2.2) { x 1 -mx, x 2 -mx,..., xn-mx,...}, а вероятности  . Легко видеть, что
. Легко видеть, что  .
. = Dx СВ Х называют математическое ожидание квадрата центрированной СВ
= Dx СВ Х называют математическое ожидание квадрата центрированной СВ  :
: . (2.2)
. (2.2) . (2.3)
. (2.3) (2.4)
(2.4) и центральные
и центральные  моменты j -го порядка определяются формулами:
моменты j -го порядка определяются формулами: ,
,  . (2.5)
. (2.5)
 . (2.9)
. (2.9) , (2.10)
, (2.10) , (2.11)
, (2.11) . (2.12)
. (2.12) (2.13)
(2.13)

 = P(Y=yj),
= P(Y=yj),  = P(X=xi).
= P(X=xi). . Если же хотя–бы для одной пары индексов (i, j) это условие не выполнено, то СВ X и Y зависимы. Свойство зависимости или независимости легко проверяется по таблице 2.3.
. Если же хотя–бы для одной пары индексов (i, j) это условие не выполнено, то СВ X и Y зависимы. Свойство зависимости или независимости легко проверяется по таблице 2.3.



 (2.15)
(2.15) ;
; ;
; = 1.
= 1.

 , а непрерывная - плотностью распределения p (x,y).
, а непрерывная - плотностью распределения p (x,y). и центральные
и центральные  моменты порядка k+l:
моменты порядка k+l: ;
; .
. (ниже, в зависимости от ситуации, будет использоваться любое из этих обозначений):
(ниже, в зависимости от ситуации, будет использоваться любое из этих обозначений):
 ,
,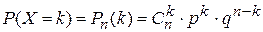 .
. получаются при разложении выражения (q + p) n по формуле бинома Ньютона (отсюда и термин «биномиальное распределение»):
получаются при разложении выражения (q + p) n по формуле бинома Ньютона (отсюда и термин «биномиальное распределение»):






 .
.
 (3.1)
(3.1)
 . (3.2)
. (3.2) ,
,






 ,
,
 (3.3)
(3.3) (3.4)
(3.4)
 ).
). .
.





