Тема 4. Моделирование одномерных временных рядов.
Похожие статьи вашей тематики
Временной ряд – это совокупность значений 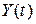 какого либо показателя какого либо показателя 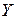 за несколько последовательных моментов времени за несколько последовательных моментов времени 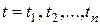 . Каждый уровень . Каждый уровень 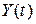 временного ряда формируется под влиянием длительных, кратковременных и случайных факторов. Для удобства временной ряд можно обозначать временного ряда формируется под влиянием длительных, кратковременных и случайных факторов. Для удобства временной ряд можно обозначать  . .
Длительные, постоянно действующие факторы оказывают на изучаемое явление определяющее влияние и формируют основную тенденцию – тренд 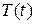 . Кратковременные, периодические факторы формируют сезонные колебания ряда . Кратковременные, периодические факторы формируют сезонные колебания ряда 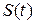 . Случайные факторы отражаются случайными изменениями уровней ряда . Случайные факторы отражаются случайными изменениями уровней ряда 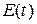 . .
Модель, в которой временной ряд представлен как сумма перечисленных компонент, т. е. 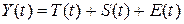 , называется аддитивной. , называется аддитивной.
Модель, в которой временной ряд представлен как произведение перечисленных компонент, т. е. 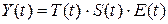 , называется мультипликативной. , называется мультипликативной.
Выбор одной из двух моделей осуществляется на основе анализа структуры сезонных колебаний. Если амплитуда сезонных колебаний приближенно постоянная, используют аддитивную модель. Если же амплитуда возрастает или уменьшается, используют мультипликативную модель.
Основная задача эконометрического исследования временного ряда – выявить каждую из перечисленных компонент ряда.
Исследование временного ряда начинают обычно с построения графика. По графику можно определить наличие тренда, сезонных колебаний а так же аддитивность (мультипликативность) модели (см. файл «Исследование Вр ряда.xls», лист 1). Если по графику трудно установить период сезонных колебаний, то это можно сделать вычислением последовательных коэффициентов автокорреляции, т. е. коэффициентов корреляции между рядом 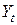 и рядами и рядами  , которые будем обозначать , которые будем обозначать 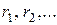 . Если наибольшее значение имеет . Если наибольшее значение имеет 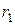 , то ряд содержит только тенденцию и не содержит сезонных колебаний. Если же наибольшее значение имеет , то ряд содержит только тенденцию и не содержит сезонных колебаний. Если же наибольшее значение имеет 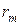 , то ряд содержит сезонные колебания с периодом , то ряд содержит сезонные колебания с периодом 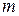 . Например, в файле «Исследование Вр ряда.xls», лист 4 наибольшее значение имеет . Например, в файле «Исследование Вр ряда.xls», лист 4 наибольшее значение имеет 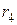 , т. е. рассматриваемый временной ряд содержит сезонные колебания с периодом 4 квартала. , т. е. рассматриваемый временной ряд содержит сезонные колебания с периодом 4 квартала.
Дальнейшее исследование временного ряда проводится по следующим алгоритмам.
АНАЛИЗ АДДИТИВНОЙ МОДЕЛИ
Построение модели 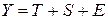 включает в себя следующие шаги: включает в себя следующие шаги:
1) выравнивание исходного ряда методом скользящей средней;
2) расчет значений сезонной компоненты;
3) устранение сезонной компоненты из исходных уровней ряда (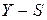 ) и получение выровненных данных ( ) и получение выровненных данных (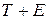 ); );
4) аналитическое выравнивание уровней (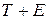 ), т. е. построение тренда ), т. е. построение тренда 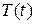 и расчет значений и расчет значений 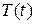 с использованием полученного уравнения тренда; с использованием полученного уравнения тренда;
5) расчет полученных по модели значений (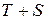 ); );
6) расчет абсолютных ошибок и качества модели.
АНАЛИЗ МУЛЬТИПЛИКАТИВНОЙ МОДЕЛИ
Построение модели  включает в себя следующие шаги: включает в себя следующие шаги:
1) выравнивание исходного ряда методом скользящей средней;
2) расчет значений сезонной компоненты;
3) устранение сезонной компоненты из исходных уровней ряда (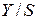 ) и получение выровненных данных ( ) и получение выровненных данных ( ); );
4) аналитическое выравнивание уровней ( ), т. е. построение тренда ), т. е. построение тренда 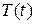 и расчет значений и расчет значений 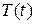 с использованием полученного уравнения тренда; с использованием полученного уравнения тренда;
5) расчет полученных по модели значений (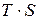 ); );
6) расчет абсолютных ошибок и качества модели.
Тема 5. Системы одновременных уравнений.
Основные понятия. Классификация систем одновременных уравнений.
Построение моделей экономических систем очень часто сводится к системам эконометрических соотношений, являющихся уравнениями и тождествами. Уравнение состоит из эндогенных и экзогенных переменных с неопределенными коэффициентами, которые следует определить по выборочным данным. Тождеством называют уравнение, не содержащее случайного члена и в котором все коэффициенты определены.
Наибольшее распространение получили системы одновременных уравнений. В таких системах одни и те же эндогенные (зависимые) переменные могут входить и в левую, и в правую части уравнений системы. Ниже буквами 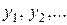 будут обозначаться эндогенные (зависимые) переменные, будут обозначаться эндогенные (зависимые) переменные,  – экзогенные (независимые) переменные. Общий вид системы одновременных уравнений – экзогенные (независимые) переменные. Общий вид системы одновременных уравнений
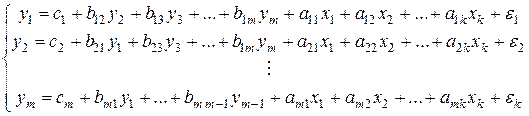 . (5.1) . (5.1)
Систему (5.1) называют так же структурной формой модели (структурной моделью). Коэффициенты структурной формы модели будем называть структурными коэффициентами. Рассмотрим некоторые частные случаи системы(5.1).
1) Система независимых уравнений характеризуется тем, что каждая эндогенная переменная выражена только через экзогенные переменные, т. е. коэффициенты 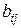 в правых частях (5.1) равны нулю. Вид системы независимых уравнений в правых частях (5.1) равны нулю. Вид системы независимых уравнений
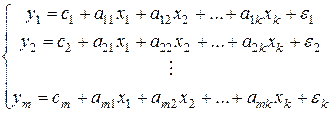 . (5.2) . (5.2)
Систему (5.2) называют так же приведенной формой модели.
2) Система рекурсивных уравнений характеризуется тем, что каждая эндогенная переменная является объясняющей в следующих за ней уравнениях:
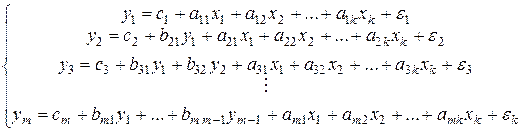 (5.3) (5.3)
Основная задача, связанная с системами одновременных уравнений состоит в определении коэффициентов  , , 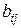 , , 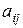 системы (5.1) по выборочным данным. Сложность этой задачи состоит в том, что в общем случае для оценки коэффициентов системы (5.1) неприменим обычный МНК, так как случайные остатки коррелируют с эндогенными переменными. Для приведенной формы модели (5.2) каждое уравнение можно рассматривать самостоятельно и к нему можно применять обычный МНК. системы (5.1) по выборочным данным. Сложность этой задачи состоит в том, что в общем случае для оценки коэффициентов системы (5.1) неприменим обычный МНК, так как случайные остатки коррелируют с эндогенными переменными. Для приведенной формы модели (5.2) каждое уравнение можно рассматривать самостоятельно и к нему можно применять обычный МНК.
Отметим, что во многих случаях систему (5.1) можно привести к (5.2). При этом коэффициенты приведенной формы модели будут нелинейными функциями структурной формы модели. После оценки коэффициентов приведенной формы по МНК возникает проблема идентификации, т. е. задача определения структурных коэффициентов через коэффициенты приведенной формы модели.
5.2. Проблема идентификации.
Возможны следующие ситуации.
1) Структурные коэффициенты однозначно выражаются через коэффициенты приведенной формы модели. В этом случае структурную модель называют точно идентифицируемой.
2) Некоторые из структурных коэффициентов не выражаются через коэффициенты приведенной формы модели. Такую структурную модель называют неидентифицируемой.
1) Структурные коэффициенты неоднозначно выражаются через коэффициенты приведенной формы модели. Тогда структурную модель называют сверхидентифицируемой.
Приведем необходимые и достаточные условия идентифицируемости (сверхидентифицируемости). Эти условия относятся к каждому уравнению структурной модели, т. е. на идентифицируемость проверяется каждое уравнение системы. Если все уравнения системы точно идентифицируемы, то система будет точно идентифицируемой. Если одно или несколько уравнений системы сверхидентифицируемы, а остальные точно идентифицируемы, то и система будет сверхидентифицируемой. Если же хотя бы одно из уравнений неидентифицируемо, то и система неидентифицируема.
Необходимое условие идентификации. Пусть 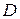 – число не включенных в уравнение, но присутствующих в системе экзогенных переменных, а – число не включенных в уравнение, но присутствующих в системе экзогенных переменных, а 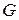 – число включенных в уравнение эндогенных переменных. Если выполнено условие – число включенных в уравнение эндогенных переменных. Если выполнено условие
 , (5.4) , (5.4)
то уравнение в структурной модели может быть идентифицировано.
В частности:
1) если 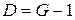 , то уравнение точно идентифицируемо (при выполнении достаточных условий идентификации); , то уравнение точно идентифицируемо (при выполнении достаточных условий идентификации);
2) если 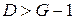 , то уравнение сверхидентифицируемо (при выполнении достаточных условий идентификации); , то уравнение сверхидентифицируемо (при выполнении достаточных условий идентификации);
3) если же 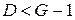 , то уравнение неидентифицируемо. , то уравнение неидентифицируемо.
Достаточное условие идентификации. Пусть для рассматриваемого уравнения выполнено необходимое условие идентификации (5.4). Выбросим (мысленно) это уравнение из системы и составим матрицу из коэффициентов при переменных (эндогенных и экзогенных), отсутствующих в исследуемом уравнении. Если ранг полученной матрицы равен 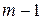 , где , где 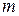 – число экзогенных переменных, то рассматриваемое уравнение идентифицируемо. – число экзогенных переменных, то рассматриваемое уравнение идентифицируемо.
Пример 5.1. Проверить на идентифицируемость каждое уравнение следующей структурной системы
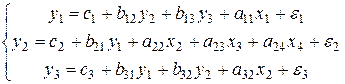 . .
В данной системе 3 эндогенные переменные 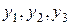 и 4 экзогенные переменные и 4 экзогенные переменные  . Предварительно проверим, удовлетворяет ли каждое из уравнений необходимому условию идентификации. . Предварительно проверим, удовлетворяет ли каждое из уравнений необходимому условию идентификации.
1-е уравнение: 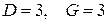 – отсутствуют три экзогенные переменные – отсутствуют три экзогенные переменные 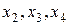 , присутствуют три эндогенные переменные , присутствуют три эндогенные переменные 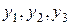 . . 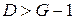 , так как 3>3–1 , так как 3>3–1 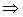 необходимое условие идентификации выполнено. необходимое условие идентификации выполнено.
2-е уравнение:  – отсутствует одна экзогенная переменная – отсутствует одна экзогенная переменная  , присутствуют две эндогенные переменные , присутствуют две эндогенные переменные 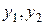 . . 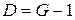 , так как 1=2–1 , так как 1=2–1 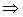 необходимое условие идентификации выполнено. необходимое условие идентификации выполнено.
3-е уравнение: 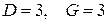 – отсутствуют три экзогенные переменные – отсутствуют три экзогенные переменные 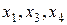 , присутствуют три эндогенные переменные , присутствуют три эндогенные переменные 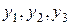 . . 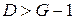 , так как 3>3–1 , так как 3>3–1 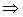 необходимое условие идентификации выполнено. необходимое условие идентификации выполнено.
Проверка выполнения достаточных условий идентификации.
1-е уравнение: матрица из коэффициентов при 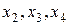 во втором и третьем уравнениях имеет вид во втором и третьем уравнениях имеет вид
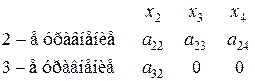 . .
Минор 2-го порядка  , т. е. ранг матрицы равен 2=3–1. Достаточные условия идентификации выполнены для 1-го уравнения. Это уравнение сверхидентифицируемо. , т. е. ранг матрицы равен 2=3–1. Достаточные условия идентификации выполнены для 1-го уравнения. Это уравнение сверхидентифицируемо.
2-е уравнение: матрица из коэффициентов при 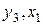 в первом и третьем уравнениях имеет вид в первом и третьем уравнениях имеет вид
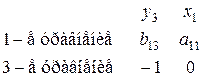 . .
Так как определитель этой матрицы 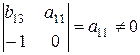 , то ее ранг равен 2=3–1. Достаточные условия идентификации выполнены для 2-го уравнения. Это уравнение точно идентифицируемо. , то ее ранг равен 2=3–1. Достаточные условия идентификации выполнены для 2-го уравнения. Это уравнение точно идентифицируемо.
3-е уравнение: матрица из коэффициентов при 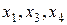 в первом и втором уравнениях имеет вид в первом и втором уравнениях имеет вид
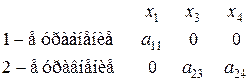 . .
Минор 2-го порядка 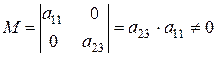 , т. е. ранг матрицы равен 2=3–1. Достаточные условия идентификации выполнены для 3-го уравнения. Это уравнение сверхидентифицируемо. , т. е. ранг матрицы равен 2=3–1. Достаточные условия идентификации выполнены для 3-го уравнения. Это уравнение сверхидентифицируемо.
Так как каждое уравнение системы идентифицируемо, причем первое и третье уравнения сверхидентифицируемы, то система сверхидентифицируема.
Приложения.
Приложение 1. Таблица значений плотности вероятности
нормального закона N(0;1).
| х
| +0.00
| +0.01
| +0.02
| +0.03
| +0.04
| +0.05
| +0.06
| +0.07
| +0.08
| +0.09
| | 0.0
| 0.3989
| .3989
| .3989
| .3988
| .3986
| .3984
| .3982
| .3980
| .3977
| .3973
| | 0.1
| .3970
| .3965
| .3961
| .3956
| .3951
| .3945
| .3939
| .3932
| .3925
| .3918
| | 0.2
| .3910
| .3902
| .3894
| .3885
| .3876
| .3867
| .3857
| .3847
| .3836
| .3825
| | 0.3
| .3814
| .3802
| .3790
| .3778
| .3765
| .3752
| .3739
| .3725
| .3712
| .3697
| | 0.4
| .3683
| .3668
| .3653
| .3637
| .3621
| .3605
| .3589
| .3572
| .3555
| .3538
| | 0.5
| .3521
| .3503
| .3485
| .3467
| .3448
| .3429
| .3410
| .3391
| .3372
| .3352
| | 0.6
| .3332
| .3312
| .3292
| .3271
| .3251
| .3230
| .3209
| .3187
| .3166
| .3144
| | 0.7
| .3123
| .3101
| .3079
| .3056
| .3034
| .3011
| .2989
| .2966
| .2943
| .2920
| | 0.8
| .2897
| .2874
| .2850
| .2827
| .2803
| .2780
| .2756
| .2732
| .2709
| .2685
| | 0.9
| .2661
| .2637
| .2613
| .2589
| .2565
| .2541
| .2516
| .2492
| .2468
| .2444
| | 1.0
| .2420
| .2396
| .2371
| .2347
| .2323
| .2299
| .2275
| .2251
| .2227
| .2203
| | 1.1
| .2179
| .2155
| .2131
| .2107
| .2083
| .2059
| .2036
| .2012
| .1989
| .1965
| | 1.2
| .1942
| .1919
| .1895
| .1872
| .1849
| .1826
| .1804
| .1781
| .1758
| .1736
| | 1.3
| .1714
| .1691
| .1669
| .1647
| .1626
| .1604
| .1582
| .1561
| .1539
| .1518
| | 1.4
| .1497
| .1476
| .1456
| .1435
| .1415
| .1394
| .1374
| .1354
| .1334
| .1315
| | 1.5
| .1295
| .1276
| .1257
| .1238
| .1219
| .1200
| .1182
| .1163
| .1145
| .1127
| | 1.6
| .1109
| .1092
| .1074
| .1057
| .1040
| .1023
| .1006
| .0989
| .0973
| .0957
| | 1.7
| .0940
| .0925
| .0909
| .0893
| .0878
| .0863
| .0848
| .0833
| .0818
| .0804
| | 1.8
| .0790
| .0775
| .0761
| .0748
| .0734
| .0721
| .0707
| .0694
| .0681
| .0669
| | 1.9
| .0656
| .0644
| .0632
| .0620
| .0608
| .0596
| .0584
| .0573
| .0562
| .0551
| | 2.2
| .0540
| .0529
| .0519
| .0508
| .0498
| .0488
| .0478
| .0468
| .0459
| .0449
| | 2.1
| .0440
| .0431
| .0422
| .0413
| .0404
| .0396
| .0387
| .0379
| .0371
| .0363
| | 2.2
| .0355
| .0347
| .0339
| .0332
| .0325
| .0317
| .0310
| .0303
| .0297
| .0290
| | 2.3
| .0283
| .0277
| .0270
| .0264
| .0258
| .0252
| .0246
| .0241
| .0235
| .0229
| | 2.4
| .0224
| .0219
| .0213
| .0208
| .0203
| .0198
| .0194
| .0189
| .0184
| .0180
| | 2.5
| .0175
| .0171
| .0167
| .0163
| .0158
| .0154
| .0151
| .0147
| .0143
| .0139
| | 2.6
| .0136
| .0132
| .0129
| .0126
| .0122
| .0119
| .0116
| .0113
| .0110
| .0107
| | 2.7
| .0104
| .0101
| .0099
| .0096
| .0093
| .0091
| .0088
| .0086
| .0084
| .0081
| | 2.8
| .0079
| .0077
| .0075
| .0073
| .0071
| .0069
| .0067
| .0065
| .0063
| .0061
| | 2.9
| .0060
| .0058
| .0056
| .0055
| .0053
| .0051
| .0050
| .0048
| .0047
| .0046
| | 3.0
| .0044
| .0043
| .0042
| .0040
| .0039
| .0038
| .0037
| .0036
| .0035
| .0034
| | 3.1
| .0033
| .0032
| .0031
| .0030
| .0029
| .0028
| .0027
| .0026
| .0025
| .0025
| | 3.2
| .0024
| .0023
| .0022
| .0022
| .0021
| .0020
| .0020
| .0019
| .0018
| .0018
| | 3.3
| .0017
| .0017
| .0016
| .0016
| .0015
| .0015
| .0014
| .0014
| .0013
| .0013
| | 3.4
| .0012
| .0012
| .0012
| .0011
| .0011
| .0010
| .0010
| .0010
| .0009
| .0009
| | 3.5
| .0009
| .0008
| .0008
| .0008
| .0008
| .0007
| .0007
| .0007
| .0007
| .0006
| | 3.6
| .0006
| .0006
| .0006
| .0005
| .0005
| .0005
| .0005
| .0005
| .0005
| .0004
| | 3.7
| .0004
| .0004
| .0004
| .0004
| .0004
| .0004
| .0003
| .0003
| .0003
| .0003
| | 3.8
| .0003
| .0003
| .0003
| .0003
| .0003
| .0002
| .0002
| .0002
| .0002
| .0002
| | 3.9
| .0002
| .0002
| .0002
| .0002
| .0002
| .0002
| .0002
| .0002
| .0001
| .0001
| | 4.0
| .0001
| .0001
| .0001
| .0001
| .0001
| .0001
| .0001
| .0001
| .00009
| .00009
|
Приложение 2. Таблица значений функции Ф (х)
| х
| Ф (х)
| х
| Ф (х)
| х
| Ф (х)
| х
| Ф (х)
| х
| Ф (х)
| | 0.00
|
| 0.45
| 0.1736
| 0.90
| 0.3159
| 1.35
| 0.4115
| 1.80
| 0.4641
| | 0.01
| 0.0040
| 0.46
| 0.1772
| 0.91
| 0.3186
| 1.36
| 0.4131
| 1.81
| 0.4649
| | 0.02
| 0.0080
| 0.47
| 0.1808
| 0.92
| 0.3212
| 1.37
| 0.4147
| 1.82
| 0.4656
| | 0.03
| 0.0120
| 0.48
| 0.1844
| 0.93
| 0.3238
| 1.38
| 0.4162
| 1.83
| 0.4664
| | 0.04
| 0.0160
| 0.49
| 0.1879
| 0.94
| 0.3264
| 1.39
| 0.4177
| 1.84
| 0.4671
| | 0.05
| 0.0199
| 0.50
| 0.1915
| 0.95
| 0.3289
| 1.40
| 0.4192
| 1.85
| 0.4678
| | 0.06
| 0.0239
| 0.51
| 0.195
| 0.96
| 0.3315
| 1.41
| 0.4207
| 1.86
| 0.4686
| | 0.07
| 0.0279
| 0.52
| 0.1985
| 0.97
| 0.334
| 1.42
| 0.4222
| 1.87
| 0.4693
| | 0.08
| 0.0319
| 0.53
| 0.2019
| 0.98
| 0.3365
| 1.43
| 0.4236
| 1.88
| 0.4699
| | 0.09
| 0.0359
| 0.54
| 0.2054
| 0.99
| 0.3389
| 1.44
| 0.4251
| 1.89
| 0.4706
| | 0.10
| 0.0398
| 0.55
| 0.2088
| 1.00
| 0.3413
| 1.45
| 0.4265
| 1.90
| 0.4713
| | 0.11
| 0.0438
| 0.56
| 0.2123
| 1.01
| 0.3438
| 1.46
| 0.4279
| 1.91
| 0.4719
| | 0.12
| 0.0478
| 0.57
| 0.2157
| 1.02
| 0.3461
| 1.47
| 0.4292
| 1.92
| 0.4726
| | 0.13
| 0.0517
| 0.58
| 0.219
| 1.03
| 0.3485
| 1.48
| 0.4306
| 1.93
| 0.4732
| | 0.14
| 0.0557
| 0.59
| 0.2224
| 1.04
| 0.3508
| 1.49
| 0.4319
| 1.94
| 0.4738
| | 0.15
| 0.0596
| 0.60
| 0.2257
| 1.05
| 0.3531
| 1.50
| 0.4332
| 1.95
| 0.4744
| | 0.16
| 0.0636
| 0.61
| 0.2291
| 1.06
| 0.3554
| 1.51
| 0.4345
| 1.96
| 0.475
| | 0.17
| 0.0675
| 0.62
| 0.2324
| 1.07
| 0.3577
| 1.52
| 0.4357
| 1.97
| 0.4756
| | 0.18
| 0.0714
| 0.63
| 0.2357
| 1.08
| 0.3599
| 1.53
| 0.437
| 1.98
| 0.4761
| | 0.19
| 0.0754
| 0.64
| 0.2389
| 1.09
| 0.3621
| 1.54
| 0.4382
| 1.99
| 0.4767
| | 0.22
| 0.0793
| 0.65
| 0.2422
| 1.10
| 0.3643
| 1.55
| 0.4394
| 2.00
| 0.4772
| | 0.21
| 0.0832
| 0.66
| 0.2454
| 1.11
| 0.3665
| 1.56
| 0.4406
| 2.01
| 0.4778
| | 0.22
| 0.0871
| 0.67
| 0.2486
| 1.12
| 0.3686
| 1.57
| 0.4418
| 2.02
| 0.4783
| | 0.23
| 0.0910
| 0.68
| 0.2517
| 1.13
| 0.3708
| 1.58
| 0.4429
| 2.03
| 0.4788
| | 0.24
| 0.0948
| 0.69
| 0.2549
| 1.14
| 0.3729
| 1.59
| 0.4441
| 2.04
| 0.4793
| | 0.25
| 0.0987
| 0.70
| 0.258
| 1.15
| 0.3749
| 1.60
| 0.4452
| 2.05
| 0.4798
| | 0.26
| 0.1026
| 0.71
| 0.2611
| 1.16
| 0.377
| 1.61
| 0.4463
| 2.06
| 0.4803
| | 0.27
| 0.1064
| 0.72
| 0.2642
| 1.17
| 0.379
| 1.62
| 0.4474
| 2.07
| 0.4808
| | 0.28
| 0.1103
| 0.73
| 0.2673
| 1.18
| 0.381
| 1.63
| 0.4484
| 2.08
| 0.4812
| | 0.29
| 0.1141
| 0.74
| 0.2704
| 1.19
| 0.383
| 1.64
| 0.4495
| 2.09
| 0.4817
| | 0.30
| 0.1179
| 0.75
| 0.2734
| 1.20
| 0.3849
| 1.65
| 0.4505
| 2.10
| 0.4821
| | 0.31
| 0.1217
| 0.76
| 0.2764
| 1.21
| 0.3869
| 1.66
| 0.4515
| 2.11
| 0.4826
| | 0.32
| 0.1255
| 0.77
| 0.2794
| 1.22
| 0.3888
| 1.67
| 0.4525
| 2.12
| 0.483
| | 0.33
| 0.1293
| 0.78
| 0.2823
| 1.23
| 0.3907
| 1.68
| 0.4535
| 2.13
| 0.4834
| | 0.34
| 0.1331
| 0.79
| 0.2852
| 1.24
| 0.3925
| 1.69
| 0.4545
| 2.14
| 0.4838
| | 0.35
| 0.1368
| 0.80
| 0.2881
| 1.25
| 0.3944
| 1.70
| 0.4554
| 2.15
| 0.4842
| | 0.36
| 0.1406
| 0.81
| 0.291
| 1.26
| 0.3962
| 1.71
| 0.4564
| 2.16
| 0.4846
| | 0.37
| 0.1443
| 0.82
| 0.2939
| 1.27
| 0.398
| 1.72
| 0.4573
| 2.17
| 0.485
| | 0.38
| 0.148
| 0.83
| 0.2967
| 1.28
| 0.3997
| 1.73
| 0.4582
| 2.18
| 0.4854
| | 0.39
| 0.1517
| 0.84
| 0.2995
| 1.29
| 0.4015
| 1.74
| 0.4591
| 2.19
| 0.4857
| | 0.40
| 0.1554
| 0.85
| 0.3023
| 1.30
| 0.4032
| 1.75
| 0.4599
| 2.20
| 0.4861
| | 0.41
| 0.1591
| 0.86
| 0.3051
| 1.31
| 0.4049
| 1.76
| 0.4608
| 2.21
| 0.4864
| | 0.42
| 0.1628
| 0.87
| 0.3078
| 1.32
| 0.4066
| 1.77
| 0.4616
| 2.22
| 0.4868
| | 0.43
| 0.1664
| 0.88
| 0.3106
| 1.33
| 0.4082
| 1.78
| 0.4625
| 2.23
| 0.4871
| | 0.44
| 0.1700
| 0.89
| 0.3133
| 1.34
| 0.4099
| 1.79
| 0.4633
| 2.24
| 0.4875
|
Таблица значений функции Ф (х) (продолжение).
| х
| Ф (х)
| х
| Ф (х)
| х
| Ф (х)
| х
| Ф (х)
| х
| Ф (х)
| | 2.25
| 0.4878
| 2.70
| 0.4965
| 3.15
| 0.4992
| 3.60
| 0.499841
| 4.05
| 0.499974
| | 2.26
| 0.4881
| 2.71
| 0.4966
| 3.16
| 0.4992
| 3.61
| 0.499847
| 4.06
| 0.499975
| | 2.27
| 0.4884
| 2.72
| 0.4967
| 3.17
| 0.4992
| 3.62
| 0.499853
| 4.07
| 0.499976
| | 2.28
| 0.4887
| 2.73
| 0.4968
| 3.18
| 0.4993
| 3.63
| 0.499858
| 4.08
| 0.499977
| | 2.29
| 0.489
| 2.74
| 0.4969
| 3.19
| 0.4993
| 3.64
| 0.499864
| 4.09
| 0.499978
| | 2.30
| 0.4893
| 2.75
| 0.4970
| 3.20
| 0.4993
| 3.65
| 0.499869
| 4.10
| 0.499979
| | 2.31
| 0.4896
| 2.76
| 0.4971
| 3.21
| 0.4993
| 3.66
| 0.499874
| 4.11
| 0.499980
| | 2.32
| 0.4898
| 2.77
| 0.4972
| 3.22
| 0.4994
| 3.67
| 0.499879
| 4.12
| 0.499981
| | 2.33
| 0.4901
| 2.78
| 0.4973
| 3.23
| 0.4994
| 3.68
| 0.499883
| 4.13
| 0.499982
| | 2.34
| 0.4904
| 2.79
| 0.4974
| 3.24
| 0.4994
| 3.69
| 0.499888
| 4.14
| 0.499983
| | 2.35
| 0.4906
| 2.80
| 0.4974
| 3.25
| 0.4994
| 3.70
| 0.499892
| 4.15
| 0.499983
| | 2.36
| 0.4909
| 2.81
| 0.4975
| 3.26
| 0.4994
| 3.71
| 0.499896
| 4.16
| 0.499984
| | 2.37
| 0.4911
| 2.82
| 0.4976
| 3.27
| 0.4995
| 3.72
| 0.499900
| 4.17
| 0.499985
| | 2.38
| 0.4913
| 2.83
| 0.4977
| 3.28
| 0.4995
| 3.73
| 0.499904
| 4.18
| 0.499985
| | 2.39
| 0.4916
| 2.84
| 0.4977
| 3.29
| 0.4995
| 3.74
| 0.499908
| 4.19
| 0.499986
| | 2.40
| 0.4918
| 2.85
| 0.4978
| 3.30
| 0.4995
| 3.75
| 0.499912
| 4.20
| 0.499987
| | 2.41
| 0.492
| 2.86
| 0.4979
| 3.31
| 0.4995
| 3.76
| 0.499915
| 4.21
| 0.499987
| | 2.42
| 0.4922
| 2.87
| 0.4979
| 3.32
| 0.4995
| 3.77
| 0.499918
| 4.22
| 0.499988
| | 2.43
| 0.4925
| 2.88
| 0.4980
| 3.33
| 0.4996
| 3.78
| 0.499922
| 4.23
| 0.499988
| | 2.44
| 0.4927
| 2.89
| 0.4981
| 3.34
| 0.4996
| 3.79
| 0.499925
| 4.24
| 0.499989
| | 2.45
| 0.4929
| 2.90
| 0.4981
| 3.35
| 0.4996
| 3.80
| 0.499928
| 4.25
| 0.499989
| | 2.46
| 0.4931
| 2.91
| 0.4982
| 3.36
| 0.4996
| 3.81
| 0.499931
| 4.26
| 0.499990
| | 2.47
| 0.4932
| 2.92
| 0.4982
| 3.37
| 0.4996
| 3.82
| 0.499933
| 4.27
| 0.499990
| | 2.48
| 0.4934
| 2.93
| 0.4983
| 3.38
| 0.4996
| 3.83
| 0.499936
| 4.28
| 0.499991
| | 2.49
| 0.4936
| 2.94
| 0.4984
| 3.39
| 0.4997
| 3.84
| 0.499938
| 4.29
| 0.499991
| | 2.50
| 0.4938
| 2.95
| 0.4984
| 3.40
| 0.4997
| 3.85
| 0.499941
| 4.30
| 0.499991
| | 2.51
| 0.494
| 2.96
| 0.4985
| 3.41
| 0.4997
| 3.86
| 0.499943
| 4.31
| 0.499992
| | 2.52
| 0.4941
| 2.97
| 0.4985
| 3.42
| 0.4997
| 3.87
| 0.499946
| 4.32
| 0.499992
| | 2.53
| 0.4943
| 2.98
| 0.4986
| 3.43
| 0.4997
| 3.88
| 0.499948
| 4.33
| 0.499993
| | 2.54
| 0.4945
| 2.99
| 0.4986
| 3.44
| 0.4997
| 3.89
| 0.499950
| 4.34
| 0.499993
| | 2.55
| 0.4946
| 3.00
| 0.4987
| 3.45
| 0.4997
| 3.90
| 0.499952
| 4.35
| 0.499993
| | 2.56
| 0.4948
| 3.01
| 0.4987
| 3.46
| 0.4997
| 3.91
| 0.499954
| 4.36
| 0.499993
| | 2.57
| 0.4949
| 3.02
| 0.4987
| 3.47
| 0.4997
| 3.92
| 0.499956
| 4.37
| 0.499994
| | 2.58
| 0.4951
| 3.03
| 0.4988
| 3.48
| 0.4997
| 3.93
| 0.499958
| 4.38
| 0.499994
| | 2.59
| 0.4952
| 3.04
| 0.4988
| 3.49
| 0.4998
| 3.94
| 0.499959
| 4.39
| 0.499994
| | 2.60
| 0.4953
| 3.05
| 0.4989
| 3.50
| 0.4998
| 3.95
| 0.499961
| 4.40
| 0.499995
| | 2.61
| 0.4955
| 3.06
| 0.4989
| 3.51
| 0.4998
| 3.96
| 0.499963
| 4.41
| 0.499995
| | 2.62
| 0.4956
| 3.07
| 0.4989
| 3.52
| 0.4998
| 3.97
| 0.499964
| 4.42
| 0.499995
| | 2.63
| 0.4957
| 3.08
| 0.4990
| 3.53
| 0.4998
| 3.98
| 0.499966
| 4.43
| 0.499995
| | 2.64
| 0.4959
| 3.09
| 0.4990
| 3.54
| 0.4998
| 3.99
| 0.499967
| 4.44
| 0.499996
| | 2.65
| 0.496
| 3.10
| 0.4990
| 3.55
| 0.4998
| 4.00
| 0.499968
| 4.45
| 0.499996
| | 2.66
| 0.4961
| 3.11
| 0.4991
| 3.56
| 0.4998
| 4.01
| 0.499970
| 4.46
| 0.499996
| | 2.67
| 0.4962
| 3.12
| 0.4991
| 3.57
| 0.4998
| 4.02
| 0.499971
| 4.47
| 0.499996
| | 2.68
| 0.4963
| 3.13
| 0.4991
| 3.58
| 0.4998
| 4.03
| 0.499972
| 4.48
| 0.499996
| | 2.69
| 0.4964
| 3.14
| 0.4992
| 3.59
| 0.4998
| 4.04
| 0.499973
| 4.49
| 0.499996
|
Приложение 3. Квантили  . .
| P
n
| 0.025
| 0.05
| 0.9
| 0.95
| 0.975
|
| P
n
| 0.025
| 0.05
| 0.9
| 0.95
| 0.975
| |
| 0.9×10–3
| 0.4×10–2
| 2.696
| 3.856
| 5.035
|
|
| 33.22
| 35.63
| 64.31
| 68.56
| 72.73
| |
| 0.0506
| 0.103
| 4.593
| 5.991
| 7.367
|
|
| 34.08
| 36.41
| 65.47
| 69.81
| 73.68
| |
| 0.216
| 0.352
| 6.249
| 7.795
| 9.309
|
|
| 34.78
| 37.27
| 66.55
| 71.04
|
| |
| 0.484
| 0.711
| 7.759
| 9.464
| 11.11
|
|
| 35.63
| 38.07
| 67.65
| 72.16
| 76.09
| |
| 0.831
| 1.15
| 9.234
| 11.06
| 12.82
|
|
| 36.35
| 38.97
| 68.79
| 73.34
| 77.32
| |
| 1.24
| 1.64
| 10.64
| 12.57
| 14.42
|
|
| 37.2
| 39.8
| 69.94
| 74.45
| 78.39
| |
| 1.65
| 2.17
| 12.02
| 14.02
| 15.97
|
|
| 37.94
| 40.61
| 71.04
| 75.6
| 79.72
| |
| 2.18
| 2.73
| 13.36
| 15.45
| 17.48
|
|
| 38.89
| 41.47
| 72.18
| 76.76
| 80.85
| |
| 2.70
| 3.33
| 14.69
| 16.87
| 18.98
|
|
| 39.63
| 42.35
| 73.25
| 77.85
| 81.96
| |
| 3.25
| 4.57
| 15.98
| 18.29
| 20.46
|
|
| 40.46
| 43.18
| 74.39
| 79.07
| 83.27
| |
| 3.823
| 4.578
| 17.28
| 19.72
| 21.86
|
|
| 41.44
| 44.04
| 75.47
| 80.34
| 84.43
| |
| 4.418
| 5.239
| 18.53
| 21.05
| 23.35
|
|
| 42.18
| 44.96
| 76.59
| 81.39
| 85.75
| |
| 5.009
| 5.889
| 19.83
| 22.35
| 24.78
|
|
| 43.06
| 45.7
| 77.74
| 82.55
| 86.85
| |
| 5.6
| 6.576
| 21.08
| 23.63
|
|
|
| 43.78
| 46.59
| 78.89
| 83.62
| 88.06
| |
| 6.212
| 7.252
| 22.3
| 24.98
| 27.46
|
|
| 44.64
| 47.4
| 79.98
| 84.81
| 89.12
| |
| 6.893
| 7.938
| 23.51
| 26.29
| 28.77
|
|
| 45.4
| 48.32
| 81.1
|
| 90.34
| |
| 7.573
| 8.696
| 24.76
| 27.57
| 30.16
|
|
| 46.25
| 49.23
| 82.2
| 87.24
| 91.38
| |
| 8.223
| 9.398
| 25.96
| 28.82
| 31.41
|
|
| 47.03
|
| 83.29
| 88.28
| 92.62
| |
| 8.86
| 10.14
| 27.2
| 30.14
| 32.82
|
|
| 47.95
| 50.87
| 84.41
| 89.36
| 93.67
| |
| 9.573
| 10.85
| 28.4
| 31.4
| 34.08
|
|
| 48.9
| 51.66
| 85.55
| 90.52
| 94.99
| |
| 10.31
| 11.63
| 29.63
| 32.68
| 35.46
|
|
| 49.68
| 52.63
| 86.64
| 91.68
| 96.1
| |
|
| 12.35
| 30.8
| 33.94
| 36.73
|
|
| 50.46
| 53.44
| 87.71
| 92.86
| 97.31
| |
| 11.7
| 13.1
| 32.03
| 35.17
| 38.06
|
|
| 51.32
| 54.32
| 88.84
| 93.87
| 98.37
| |
| 12.43
| 13.87
| 33.2
| 36.39
| 39.29
|
|
| 52.1
| 55.17
|
| 95.08
| 99.66
| |
| 13.13
| 14.63
| 34.35
| 37.65
| 40.63
|
|
| 53.03
| 55.97
| 91.07
| 96.14
| 100.8
| |
| 13.88
| 15.4
| 35.54
| 38.86
| 41.87
|
|
| 53.72
| 56.94
| 92.24
| 97.32
| 101.9
| |
| 14.6
| 16.11
| 36.72
| 40.04
| 43.09
|
|
| 54.61
| 57.78
| 93.29
| 98.38
|
| |
| 15.32
| 16.91
| 37.91
| 41.32
| 44.44
|
|
| 55.39
| 58.62
| 94.35
| 99.61
| 104.3
| |
|
| 17.72
| 39.07
| 42.53
| 45.69
|
|
| 56.34
| 59.51
| 95.47
| 100.7
| 105.4
| |
| 16.76
| 18.48
| 40.22
| 43.72
| 46.92
|
|
| 57.3
| 60.31
| 96.57
| 101.8
| 106.5
| |
| 17.56
| 19.29
| 41.42
| 44.91
| 48.3
|
|
| 58.05
| 61.25
| 97.66
|
| 107.7
| |
| 18.37
| 20.07
| 42.59
| 46.29
| 49.45
|
|
| 58.96
| 62.07
| 98.78
| 104.1
| 108.8
| |
| 19.06
| 20.86
| 43.75
| 47.41
| 50.68
|
|
| 59.7
| 62.99
| 99.92
| 105.3
| 110.1
| |
| 19.81
| 21.66
| 44.88
| 48.63
| 51.91
|
|
| 60.56
| 63.83
|
| 106.3
| 111.2
| |
| 20.62
| 22.42
| 46.11
| 49.8
| 53.19
|
|
| 61.37
| 64.76
| 102.2
| 107.5
| 112.3
| |
| 21.26
| 23.29
| 47.22
| 50.93
| 54.39
|
|
| 62.13
| 65.67
| 103.2
| 108.5
| 113.3
| |
| 22.06
| 24.06
| 48.39
| 52.14
| 55.55
|
|
| 63.06
| 66.49
| 104.2
| 109.8
| 114.7
| |
| 22.91
| 24.88
| 49.49
| 53.37
| 56.87
|
|
| 63.82
| 67.31
| 105.4
| 110.9
| 115.8
| |
| 23.62
| 25.7
| 50.63
| 54.54
| 58.07
|
|
| 64.84
| 68.23
| 106.4
|
| 116.9
| |
| 24.38
| 26.5
| 51.79
| 55.68
| 59.24
|
|
| 65.63
| 69.13
| 107.5
| 113.1
|
| |
| 25.23
| 27.37
| 52.96
| 56.96
| 60.54
|
|
| 66.51
|
| 108.7
| 114.4
| 119.2
| |
| 26.09
| 28.15
| 54.05
| 58.18
| 61.74
|
|
| 67.45
| 70.93
| 109.8
| 115.4
| 120.4
| |
| 26.81
| 28.95
| 55.23
| 59.26
| 62.85
|
|
| 68.24
| 71.73
| 110.9
| 116.5
| 121.4
| |
| 27.6
| 29.78
| 56.39
| 60.47
| 64.17
|
|
| 69.14
| 72.53
| 111.9
| 117.7
| 122.7
| |
| 28.38
| 30.58
| 57.51
| 61.64
| 65.33
|
|
| 69.93
| 73.5
|
| 118.7
| 123.7
| |
| 29.13
| 31.45
| 58.65
| 62.74
| 66.45
|
|
| 70.83
| 74.33
| 114.2
| 119.9
|
| |
| 29.94
| 32.34
| 59.77
| 63.99
| 67.79
|
|
| 71.61
| 75.3
| 115.2
| 120.9
| 126.1
| |
| 30.66
| 33.06
| 60.86
| 65.13
| 68.96
|
|
| 72.37
| 76.22
| 116.3
| 122.1
| 127.2
| |
| 31.61
| 33.91
| 62.01
| 66.26
| 70.11
|
|
| 73.33
| 77.03
| 117.4
| 123.2
| 128.3
| |
| 32.31
| 34.78
| 63.16
| 67.5
| 71.24
|
|
| 74.1
| 77.87
| 118.5
| 124.2
| 129.3
|
|



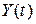 какого либо показателя
какого либо показателя 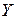 за несколько последовательных моментов времени
за несколько последовательных моментов времени 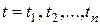 . Каждый уровень
. Каждый уровень  .
.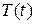 . Кратковременные, периодические факторы формируют сезонные колебания ряда
. Кратковременные, периодические факторы формируют сезонные колебания ряда 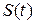 . Случайные факторы отражаются случайными изменениями уровней ряда
. Случайные факторы отражаются случайными изменениями уровней ряда 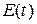 .
.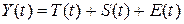 , называется аддитивной.
, называется аддитивной.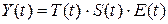 , называется мультипликативной.
, называется мультипликативной.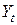 и рядами
и рядами  , которые будем обозначать
, которые будем обозначать 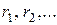 . Если наибольшее значение имеет
. Если наибольшее значение имеет 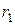 , то ряд содержит только тенденцию и не содержит сезонных колебаний. Если же наибольшее значение имеет
, то ряд содержит только тенденцию и не содержит сезонных колебаний. Если же наибольшее значение имеет 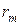 , то ряд содержит сезонные колебания с периодом
, то ряд содержит сезонные колебания с периодом 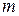 . Например, в файле «Исследование Вр ряда.xls», лист 4 наибольшее значение имеет
. Например, в файле «Исследование Вр ряда.xls», лист 4 наибольшее значение имеет 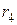 , т. е. рассматриваемый временной ряд содержит сезонные колебания с периодом 4 квартала.
, т. е. рассматриваемый временной ряд содержит сезонные колебания с периодом 4 квартала.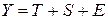 включает в себя следующие шаги:
включает в себя следующие шаги: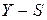 ) и получение выровненных данных (
) и получение выровненных данных (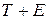 );
);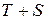 );
); включает в себя следующие шаги:
включает в себя следующие шаги: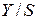 ) и получение выровненных данных (
) и получение выровненных данных ( );
);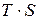 );
);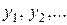 будут обозначаться эндогенные (зависимые) переменные,
будут обозначаться эндогенные (зависимые) переменные,  – экзогенные (независимые) переменные. Общий вид системы одновременных уравнений
– экзогенные (независимые) переменные. Общий вид системы одновременных уравнений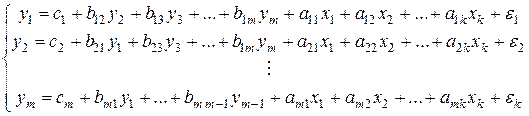 . (5.1)
. (5.1)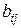 в правых частях (5.1) равны нулю. Вид системы независимых уравнений
в правых частях (5.1) равны нулю. Вид системы независимых уравнений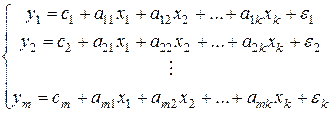 . (5.2)
. (5.2)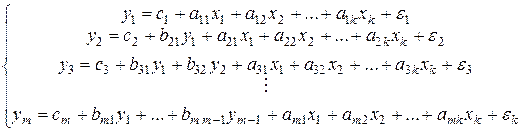 (5.3)
(5.3) ,
, 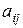 системы (5.1) по выборочным данным. Сложность этой задачи состоит в том, что в общем случае для оценки коэффициентов системы (5.1) неприменим обычный МНК, так как случайные остатки коррелируют с эндогенными переменными. Для приведенной формы модели (5.2) каждое уравнение можно рассматривать самостоятельно и к нему можно применять обычный МНК.
системы (5.1) по выборочным данным. Сложность этой задачи состоит в том, что в общем случае для оценки коэффициентов системы (5.1) неприменим обычный МНК, так как случайные остатки коррелируют с эндогенными переменными. Для приведенной формы модели (5.2) каждое уравнение можно рассматривать самостоятельно и к нему можно применять обычный МНК.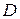 – число не включенных в уравнение, но присутствующих в системе экзогенных переменных, а
– число не включенных в уравнение, но присутствующих в системе экзогенных переменных, а 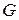 – число включенных в уравнение эндогенных переменных. Если выполнено условие
– число включенных в уравнение эндогенных переменных. Если выполнено условие , (5.4)
, (5.4)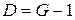 , то уравнение точно идентифицируемо (при выполнении достаточных условий идентификации);
, то уравнение точно идентифицируемо (при выполнении достаточных условий идентификации);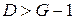 , то уравнение сверхидентифицируемо (при выполнении достаточных условий идентификации);
, то уравнение сверхидентифицируемо (при выполнении достаточных условий идентификации);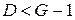 , то уравнение неидентифицируемо.
, то уравнение неидентифицируемо.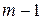 , где
, где 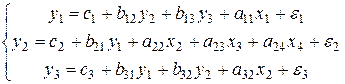 .
.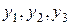 и 4 экзогенные переменные
и 4 экзогенные переменные  . Предварительно проверим, удовлетворяет ли каждое из уравнений необходимому условию идентификации.
. Предварительно проверим, удовлетворяет ли каждое из уравнений необходимому условию идентификации.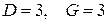 – отсутствуют три экзогенные переменные
– отсутствуют три экзогенные переменные 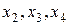 , присутствуют три эндогенные переменные
, присутствуют три эндогенные переменные 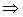 необходимое условие идентификации выполнено.
необходимое условие идентификации выполнено. – отсутствует одна экзогенная переменная
– отсутствует одна экзогенная переменная 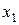 , присутствуют две эндогенные переменные
, присутствуют две эндогенные переменные 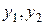 .
. 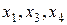 , присутствуют три эндогенные переменные
, присутствуют три эндогенные переменные 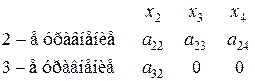 .
. , т. е. ранг матрицы равен 2=3–1. Достаточные условия идентификации выполнены для 1-го уравнения. Это уравнение сверхидентифицируемо.
, т. е. ранг матрицы равен 2=3–1. Достаточные условия идентификации выполнены для 1-го уравнения. Это уравнение сверхидентифицируемо. в первом и третьем уравнениях имеет вид
в первом и третьем уравнениях имеет вид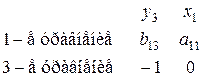 .
.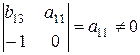 , то ее ранг равен 2=3–1. Достаточные условия идентификации выполнены для 2-го уравнения. Это уравнение точно идентифицируемо.
, то ее ранг равен 2=3–1. Достаточные условия идентификации выполнены для 2-го уравнения. Это уравнение точно идентифицируемо.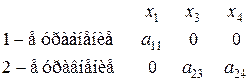 .
.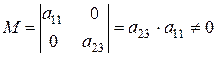 , т. е. ранг матрицы равен 2=3–1. Достаточные условия идентификации выполнены для 3-го уравнения. Это уравнение сверхидентифицируемо.
, т. е. ранг матрицы равен 2=3–1. Достаточные условия идентификации выполнены для 3-го уравнения. Это уравнение сверхидентифицируемо. .
.


