
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Эконометрические модели их свойства и классификация.Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте ЭКОНОМЕТРИКА
Введение. Модель и моделирование. Эконометрические модели их свойства и классификация. Переменные в моделях и их типы. Этапы моделирования. Эконометрика – наука, изучающая количественные закономерности и взаимозависимости в экономике методами математической статистики. Можно считать, что эконометрика – «экономика» + «метрика». Это наука об измерении и анализе экономических явлений, о количественных выражениях тех связей и соотношений, которые раскрыты и обоснованы экономической теорией. Это сплав четырех компонент: экономической теории, статистических и математических методов, компьютерных вычислений. Основная задача курса «Эконометрика» – обучение будущих экономистов методам исследования экономических процессов, основанных на использовании реальных статистических данных и на положениях экономической теории. При изучении взаимосвязей между экономическими показателями применяются положения экономической теории, затем на основе выборочных (статистических) данных строятся модели, проводится оценка их составляющих. Итоговые результаты используются для прогнозирования, принятия решений и уточнения первоначальных положений. Основной особенностью эконометрических моделей является наличие в них случайных составляющих, обусловленное неучтенными факторами, ошибками измерений и др. При этом особую важность приобретает использование основ теории вероятностей и статистики. Модель – объект любой природы, который создается исследователем с целью получения новых знаний об объекте-оригинале и отражает только существенные (с точки зрения разработчика) свойства оригинала. Эконометрическая модель – вероятностно – статистическая модель, описывающая механизм функционирования экономической или социально – экономической системы. Можно выделить три основных класса эконометрических моделей: регрессионные модели с одним уравнением, модели временных рядов и системы одновременных уравнений. В регрессионных моделях с одним уравнением объясняемая переменная представляется в виде функции от объясняющих переменных. По виду функции регрессионные модели делятся на линейные и нелинейные. К моделям временных рядов относятся модели тренда и модели сезонности. Тренд представляет собой устойчивое изменение уровня показателя в течение длительного периода времени. Сезонность характеризует устойчивые колебания уровня показателя в течение небольшого промежутка времени (месяца, квартала, года). Системы одновременных уравнений описываются системами уравнений, состоящими из тождеств и регрессионных уравнений, в каждом из которых аргументы содержат не только объясняющие переменные, но и объясняемые из других уравнений системы. Моделирование – процесс построения, изучения и применения моделей. Экзогенные переменные в модели – переменные, задаваемые «извне», автономно от модели, управляемые и планируемые. Эндогенные переменные модели – переменные, значения которых формируются в процессе и внутри функционирования анализируемой социально – экономической системы в существенной мере под воздействием экзогенных переменных и во взаимодействии друг с другом. В эконометрическом моделировании являются предметом объяснения. Лаговые переменные – это те переменные (экзогенные или эндогенные), значения которых рассматриваются в различные моменты времени, разделенные некоторым промежутком (лагом). Значения эндогенных переменных в предыдущие моменты времени могут заранее задаваться или вычисляться по уравнениям модели. Тогда эти эндогенные переменные играют роль экзогенных (объясняющих). Предопределенные переменные модели – все экзогенные переменные модели и лаговые значения эндогенных переменных, которые служат для нахождения значений эндогенных переменных в данный момент времени. Укажем основные этапы эконометрического исследования. 1. Постановочный. Формулируется цель исследования, определяется набор участвующих в модели экономических переменных. Целью исследования могут быть анализ процесса, прогноз экономических показателей, анализ возможного развития явления при различных значениях экзогенных переменных, выработка управленческих решений. При выборе переменных необходимо теоретическое обоснование каждой экономической переменной. 2. Априорный. Проводится анализ сущности изучаемого объекта, формирование и формализация известной до начала исследования информации. 3. Информационный. Осуществляется сбор необходимой статистической информации, значений экономических переменных. 4. Спецификация модели. В математической форме выражаются обнаруженные связи и соотношения, устанавливается состав экзогенных и эндогенных переменных; формируются исходные предпосылки и ограничения модели. Успех эконометрического моделирования зависит от точности выполненной задачи спецификации. 5. Параметризация. Оцениваются параметры (коэффициенты) выбранной зависимости на основе имеющихся статистических данных. 6. Идентификация. Осуществляется статистический анализ модели и оценка ее параметров. 7. Верификация. Проводится проверка адекватности модели, выясняется, насколько удачно решены проблемы спецификации, идентификации, какова точность расчетов по данной модели, насколько соответствует построенная модель реальному экономическому процессу.
Тема 1. Выборки и оценки. 1.1. Генеральная совокупность и выборка. Основные соглашения Под генеральной совокупностью (ГС) понимают множество элементов произвольной природы, подлежащих обследованию по одному или нескольким признакам. Каждый из признаков является СВ, распределенной по некоторому закону. Примером обследования ГС может служить республиканская перепись населения. В этом примере каждый объект (человек) обследовался по многим признакам (возраст, образование, социальное положение и др.). Современная МС оформилась и развивалась под давлением практических потребностей. При решении многочисленных практических задач статистики столкнулись с необходимостью изучения полных ГС с большим числом составляющих ее элементов, не имея реальной возможности изучать каждый элемент в отдельности. Например, современное промышленное предприятие, производящее в массовом масштабе различные типы промышленных изделий, не располагает возможностью установить качество производимой продукции, изучая каждое изделие в отдельности при его изготовлении или при передаче потребителю. В подобных случаях установили, что выходом для заинтересованного лица является изучение ограниченного числа элементов – части всей ГС – в надежде, что полученная таким путем информация будет полезной и достаточно точной для того, чтобы судить о качестве всей совокупности изделий. Во многих случаях, например, при статистическом контроле качества выпускаемой продукции, когда обследование каждого элемента приводит к его полному уничтожению, обследование всей ГС не имеет смысла. Часть элементов ГС, отобранных для обследования, называется выборкой. Количество отобранных элементов называют объемом выборки. Обычно n – объем выборки (количество наблюдений). В результате обследования выборки по некоторому признаку X получаем n значений исследуемого признака: x 1, x 2 ,...,xn. В МС рассматривают конкретную и математическую выборки. Конкретная выборка представляет собой совокупность из n чисел, с которыми можно производить различные вычислительные операции. Для объяснения понятия математической выборки мысленно представим себе, что из одной и той же ГС произведены другие выборки объема n. В результате обследования выборок получаем таблицу значений (верхний индекс означает номер выборки): x 1(1), x 2(1) ,...,xn (1) x 1(2), x 2(2) ,...,xn (2) ... x 1 (k), x 2 (k),...,xn(k) ... Из таблицы видно, что i -е число конкретной выборки является значением некоторой СВ Xi, так как в разных выборках на i -м месте могут стоять, вообще говоря, различные числа. В связи с этим под математической выборкой будем понимать систему СВ (X 1, X 2 ,..., Xn),компоненты которой Xi, i = 1,2,..., n удовлетворяют нижеследующим условиям А) и Б). А) Компонента Xi имеет такое же распределение, как и признак в ГС. Б) Xi - взаимно независимые СВ. Условие А) означает следующее: каждое выборочное значение является опытной реализацией одной и той же СВ X - изучаемого признака ГС. Поэтому нет оснований считать, что условие А) не выполняется. Принятие условия Б) обусловлено удобством различных теоретических выводов. На практике оно не всегда выполнено.
1.2. Способы оценивания и их свойства. Как правило, на практике мы не знаем точного вероятностного распределения (дискретного признака) или плотности распределения вероятностей (непрерывного признака). Это означает, что неизвестны также и теоретическое среднее и дисперсия. Мы, тем не менее, можем нуждаться в оценках этих или других характеристик ГС. Обычно способ оценивания представляет собой формулу для оценивания параметров ГС: Естественно потребовать, чтобы значения оценки по каждой выборке были близки к истинному значению оцениваемого параметра, которое будем обозначать q и которого мы не знаем. Обычно к оценкам параметров ГС, которые являются случайными величинами, выдвигаются следующие требования. а1) Несмещенность. q* называется несмещенной оценкой q, если М (q*) = q. (1.1) а2) Эффективность. Можно получить несколько несмещенных оценок одного и того же параметра. Среди них следует выбрать оценку с наименьшей дисперсией, которую называют эффективной. а3) Состоятельность. q* называется состоятельной оценкой q, если с увеличением объема выборки оценка q* приближается к истинному значению q. Формально это записывается с помощью предела по вероятности: для любого e>0
Соотношения (1.2) можно записать так же в виде равенства
левая часть которого и означает предел по вероятности. Отметим, что предел по вероятности обладает свойствами обычного предела функции: постоянную можно выносить за знак предела Очень часто, для проверки состоятельности оценок используются теорема Чебышева (закон больших чисел) и центральная предельная теорема. Теорема Чебышева (частный случай). Пусть
Центральная предельная теорема. Пусть
Тогда закон распределения СВ
Примеры построения оценок. Пример 1.1. Оценка математического ожидания
Рассмотрим далее свойство эффективности оценок. Для этого предположим, что найдено несколько несмещенных независимых оценок
= Из условия минимальности дисперсии получаем
= В результате получаем задачу на условный экстремум для функции
Для решения задачи по методу Лагранжа, составляем функцию Лагранжа
Необходимые условия экстремума
Так как Проведенные рассуждения позволяют сделать следующее заключение. Дисперсия оценки Применим теорему Чебышева к выборке
Отсюда следует, что оценка Пример 1.2. Оценка дисперсии
Для проверки несмещенности найдем математическое ожидание оценки:
Таким образом, оценка генеральной дисперсии с помощью выборочной дисперсии является смещенной. Чтобы получить несмещенную оценку дисперсии, выборочную дисперсию следует умножить на поправочный коэффициент Для проверки состоятельности оценки Пример 1.3. Оценка ковариации
где сумма берется по всем элементам ГС,
Покажем, что несмещенной оценкой ковариации является выборочный корреляционный момент
Предварительно преобразуем это выражение
Заменяя
Из (1.6) следует, что математическое ожидание каждого слагаемого 1-й суммы равно
т. е. Состоятельность оценки
Предел по вероятности 1-й суммы в (1.7) равен
АНАЛИЗ АДДИТИВНОЙ МОДЕЛИ Построение модели 1) выравнивание исходного ряда методом скользящей средней; 2) расчет значений сезонной компоненты; 3) устранение сезонной компоненты из исходных уровней ряда ( 4) аналитическое выравнивание уровней ( 5) расчет полученных по модели значений ( 6) расчет абсолютных ошибок и качества модели.
Основные понятия. Классификация систем одновременных уравнений. Построение моделей экономических систем очень часто сводится к системам эконометрических соотношений, являющихся уравнениями и тождествами. Уравнение состоит из эндогенных и экзогенных переменных с неопределенными коэффициентами, которые следует определить по выборочным данным. Тождеством называют уравнение, не содержащее случайного члена и в котором все коэффициенты определены. Наибольшее распространение получили системы одновременных уравнений. В таких системах одни и те же эндогенные (зависимые) переменные могут входить и в левую, и в правую части уравнений системы. Ниже буквами
Систему (5.1) называют так же структурной формой модели (структурной моделью). Коэффициенты структурной формы модели будем называть структурными коэффициентами. Рассмотрим некоторые частные случаи системы(5.1). 1) Система независимых уравнений характеризуется тем, что каждая эндогенная переменная выражена только через экзогенные переменные, т. е. коэффициенты
Систему (5.2) называют так же приведенной формой модели. 2) Система рекурсивных уравнений характеризуется тем, что каждая эндогенная переменная является объясняющей в следующих за ней уравнениях:
Основная задача, связанная с системами одновременных уравнений состоит в определении коэффициентов Отметим, что во многих случаях систему (5.1) можно привести к (5.2). При этом коэффициенты приведенной формы модели будут нелинейными функциями структурной формы модели. После оценки коэффициентов приведенной формы по МНК возникает проблема идентификации, т. е. задача определения структурных коэффициентов через коэффициенты приведенной формы модели.
5.2. Проблема идентификации. Возможны следующие ситуации. 1) Структурные коэффициенты однозначно выражаются через коэффициенты приведенной формы модели. В этом случае структурную модель называют точно идентифицируемой. 2) Некоторые из структурных коэффициентов не выражаются через коэффициенты приведенной формы модели. Такую структурную модель называют неидентифицируемой. 1) Структурные коэффициенты неоднозначно выражаются через коэффициенты приведенной формы модели. Тогда структурную модель называют сверхидентифицируемой. Приведем необходимые и достаточные условия идентифицируемости (сверхидентифицируемости). Эти условия относятся к каждому уравнению структурной модели, т. е. на идентифицируемость проверяется каждое уравнение системы. Если все уравнения системы точно идентифицируемы, то система будет точно идентифицируемой. Если одно или несколько уравнений системы сверхидентифицируемы, а остальные точно идентифицируемы, то и система будет сверхидентифицируемой. Если же хотя бы одно из уравнений неидентифицируемо, то и система неидентифицируема. Необходимое условие идентификации. Пусть
то уравнение в структурной модели может быть идентифицировано. В частности: 1) если 2) если 3) если же Достаточное условие идентификации. Пусть для рассматриваемого уравнения выполнено необходимое условие идентификации (5.4). Выбросим (мысленно) это уравнение из системы и составим матрицу из коэффициентов при переменных (эндогенных и экзогенных), отсутствующих в исследуемом уравнении. Если ранг полученной матрицы равен Пример 5.1. Проверить на идентифицируемость каждое уравнение следующей структурной системы
В данной системе 3 эндогенные переменные 1-е уравнение: 2-е уравнение: 3-е уравнение: Проверка выполнения достаточных условий идентификации. 1-е уравнение: матрица из коэффициентов при
Минор 2-го порядка 2-е уравнение: матрица из коэффициентов при
Так как определитель этой матрицы 3-е уравнение: матрица из коэффициентов при
Минор 2-го порядка Так как каждое уравнение системы идентифицируемо, причем первое и третье уравнения сверхидентифицируемы, то система сверхидентифицируема.
Приложения. Приложение 1. Таблица значений плотности вероятности нормального закона N(0;1).
Приложение 2. Таблица значений функции Ф (х)
|

 . Более конкретно, оценкой параметра q по выборке
. Более конкретно, оценкой параметра q по выборке  называется произвольная функция
называется произвольная функция  от выборочных значений. Так как предполагаемые выборочные значения
от выборочных значений. Так как предполагаемые выборочные значения  , которые будут использованы для получения численной оценки параметра q. Таким образом, метод оценивания – формула, оценка – число. Если будут извлекаться другие выборки, то метод оценивания будет один и тот же, а оценки могут меняться от выборки к выборке.
, которые будут использованы для получения численной оценки параметра q. Таким образом, метод оценивания – формула, оценка – число. Если будут извлекаться другие выборки, то метод оценивания будет один и тот же, а оценки могут меняться от выборки к выборке. или
или  . (1.2)
. (1.2) ,
, ; пределы арифметических операций (суммы, произведения, частного нескольких СВ) находятся по обычным формулам.
; пределы арифметических операций (суммы, произведения, частного нескольких СВ) находятся по обычным формулам. – независимые и одинаково распределенные СВ с математическими ожиданиями
– независимые и одинаково распределенные СВ с математическими ожиданиями  и дисперсиями
и дисперсиями  . Тогда
. Тогда . (1.3)
. (1.3) и
и  :
: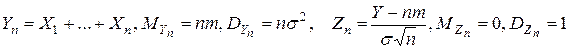 .
. к нормальному закону с параметрами 0 и 1.
к нормальному закону с параметрами 0 и 1. признака
признака  в ГС. Пусть
в ГС. Пусть  равно
равно 
 , т. е. каждая выборочная компонента может служить несмещенной оценкой неизвестной величины
, т. е. каждая выборочная компонента может служить несмещенной оценкой неизвестной величины  .
. параметра
параметра  , т. е. равна дисперсии признака
, т. е. равна дисперсии признака  , удовлетворяющую условиям несмещенности и минимальности дисперсии параметра
, удовлетворяющую условиям несмещенности и минимальности дисперсии параметра  . Из требования несмещенности
. Из требования несмещенности =
= .
.

 переменных:
переменных: при условии
при условии  .
. .
.
 , то точка
, то точка  является точкой условного минимума функции
является точкой условного минимума функции  , т.е. оценка
, т.е. оценка  , равную
, равную  .
. , равная
, равная  , обладает свойством минимальности, т. е.
, обладает свойством минимальности, т. е.  . (1.4)
. (1.4) признака
признака 


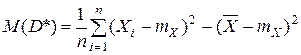 . (1.5)
. (1.5) .
. , т. е. вместо выборочной дисперсии
, т. е. вместо выборочной дисперсии  для оценки следует взять исправленную выборочную дисперсию
для оценки следует взять исправленную выборочную дисперсию  .
.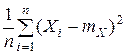 является средним арифметическим
является средним арифметическим  независимых, одинаково распределенных СВ
независимых, одинаково распределенных СВ  . По закону больших чисел
. По закону больших чисел  . Для второго слагаемого
. Для второго слагаемого  . Отсюда следует, что
. Отсюда следует, что  , т. е.
, т. е.  , то
, то  =
= 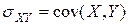 признаков
признаков  в ГС. Ковариация (корреляционный момент) между СВ
в ГС. Ковариация (корреляционный момент) между СВ  определяется как математическое ожидание произведения центрированных СВ:
определяется как математическое ожидание произведения центрированных СВ: ,
, – объем ГС. Рассмотрим выборку объема
– объем ГС. Рассмотрим выборку объема  . По основным соглашениям
. По основным соглашениям . (1.6)
. (1.6) .
.

 . (1.7)
. (1.7) ,
,  , получаем
, получаем .
. . Так как в 1-й сумме
. Так как в 1-й сумме  . Во второй сумме
. Во второй сумме  слагаемых, причем для
слагаемых, причем для  ) математическое ожидание равно
) математическое ожидание равно  и
и ,
, является несмещенной оценкой для
является несмещенной оценкой для  при оценке дисперсии. Выражение
при оценке дисперсии. Выражение  является средним арифметическим
является средним арифметическим  . По закону больших чисел
. По закону больших чисел .
. . Пределы по вероятности остальных слагаемых в (1.7) равны нулю.
. Пределы по вероятности остальных слагаемых в (1.7) равны нулю.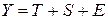 включает в себя следующие шаги:
включает в себя следующие шаги: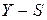 ) и получение выровненных данных (
) и получение выровненных данных (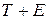 );
);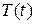 и расчет значений
и расчет значений 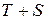 );
);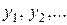 будут обозначаться эндогенные (зависимые) переменные,
будут обозначаться эндогенные (зависимые) переменные,  – экзогенные (независимые) переменные. Общий вид системы одновременных уравнений
– экзогенные (независимые) переменные. Общий вид системы одновременных уравнений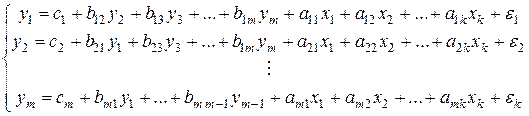 . (5.1)
. (5.1)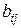 в правых частях (5.1) равны нулю. Вид системы независимых уравнений
в правых частях (5.1) равны нулю. Вид системы независимых уравнений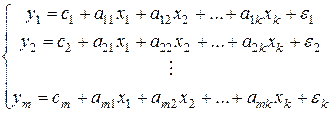 . (5.2)
. (5.2)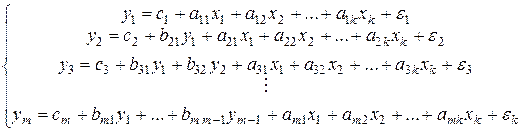 (5.3)
(5.3) ,
, 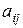 системы (5.1) по выборочным данным. Сложность этой задачи состоит в том, что в общем случае для оценки коэффициентов системы (5.1) неприменим обычный МНК, так как случайные остатки коррелируют с эндогенными переменными. Для приведенной формы модели (5.2) каждое уравнение можно рассматривать самостоятельно и к нему можно применять обычный МНК.
системы (5.1) по выборочным данным. Сложность этой задачи состоит в том, что в общем случае для оценки коэффициентов системы (5.1) неприменим обычный МНК, так как случайные остатки коррелируют с эндогенными переменными. Для приведенной формы модели (5.2) каждое уравнение можно рассматривать самостоятельно и к нему можно применять обычный МНК.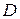 – число не включенных в уравнение, но присутствующих в системе экзогенных переменных, а
– число не включенных в уравнение, но присутствующих в системе экзогенных переменных, а 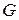 – число включенных в уравнение эндогенных переменных. Если выполнено условие
– число включенных в уравнение эндогенных переменных. Если выполнено условие , (5.4)
, (5.4)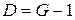 , то уравнение точно идентифицируемо (при выполнении достаточных условий идентификации);
, то уравнение точно идентифицируемо (при выполнении достаточных условий идентификации);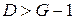 , то уравнение сверхидентифицируемо (при выполнении достаточных условий идентификации);
, то уравнение сверхидентифицируемо (при выполнении достаточных условий идентификации);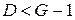 , то уравнение неидентифицируемо.
, то уравнение неидентифицируемо.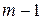 , где
, где 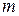 – число экзогенных переменных, то рассматриваемое уравнение идентифицируемо.
– число экзогенных переменных, то рассматриваемое уравнение идентифицируемо.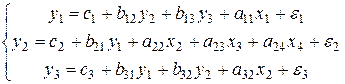 .
.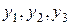 и 4 экзогенные переменные
и 4 экзогенные переменные  . Предварительно проверим, удовлетворяет ли каждое из уравнений необходимому условию идентификации.
. Предварительно проверим, удовлетворяет ли каждое из уравнений необходимому условию идентификации.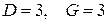 – отсутствуют три экзогенные переменные
– отсутствуют три экзогенные переменные 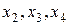 , присутствуют три эндогенные переменные
, присутствуют три эндогенные переменные 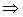 необходимое условие идентификации выполнено.
необходимое условие идентификации выполнено. – отсутствует одна экзогенная переменная
– отсутствует одна экзогенная переменная 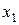 , присутствуют две эндогенные переменные
, присутствуют две эндогенные переменные 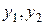 .
. 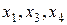 , присутствуют три эндогенные переменные
, присутствуют три эндогенные переменные 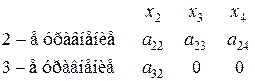 .
. , т. е. ранг матрицы равен 2=3–1. Достаточные условия идентификации выполнены для 1-го уравнения. Это уравнение сверхидентифицируемо.
, т. е. ранг матрицы равен 2=3–1. Достаточные условия идентификации выполнены для 1-го уравнения. Это уравнение сверхидентифицируемо.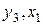 в первом и третьем уравнениях имеет вид
в первом и третьем уравнениях имеет вид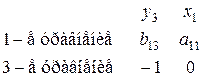 .
.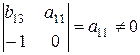 , то ее ранг равен 2=3–1. Достаточные условия идентификации выполнены для 2-го уравнения. Это уравнение точно идентифицируемо.
, то ее ранг равен 2=3–1. Достаточные условия идентификации выполнены для 2-го уравнения. Это уравнение точно идентифицируемо.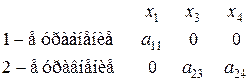 .
.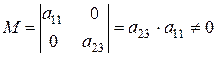 , т. е. ранг матрицы равен 2=3–1. Достаточные условия идентификации выполнены для 3-го уравнения. Это уравнение сверхидентифицируемо.
, т. е. ранг матрицы равен 2=3–1. Достаточные условия идентификации выполнены для 3-го уравнения. Это уравнение сверхидентифицируемо.


