
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Раздел 3. Моделирование в экологииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В каждой естественной науке заключено столько истины, сколько в ней есть математики. И. Кант
Глава 9. Динамические модели Глава 10. Стохастические модели Глава 11. Оптимизационные и игровые модели Глава 12. Системный анализ и управление в экологии
Глава 9. Динамические модели
Понятие моделирования
Прежде всего, следует дать определение модели. Однако это не так просто, поэтому сначала приведем несколько примеров, поясняющих, что такое модель, а затем, когда некоторое интуитивное представление о понятии «модель» сформируется, дадим определение, а также коротко опишем математические методы, с которыми связано рассмотрение тех или иных моделей. Исходным пунктом исследования, его отправной точкой, служит некоторая задача из той или иной предметной области (в данном случае из экологии или безопасности жизнедеятельности). Процесс построения модели называется моделированием. Существует несколько приемов моделирования, которые можно условно разделить на две большие группы: материальное и идеальное моделирование. К материальным относятся такие способы моделирования, при которых исследование ведется по модели, воспроизводящей основные геометрические, физические, динамические и функциональные характеристики изучаемого объекта. Из разновидностей материального моделирования выделим физическое и аналоговое моделирование. Физическим принято называть моделирование, при котором реальному объекту противопоставляется его уменьшенная (реже увеличенная) копия, допускающая лабораторное исследование и позволяющая переносить установленные свойства на реальный объект с помощью теории подобия. Типичный пример физического моделирования – исследование уменьшенной копии летательного аппарата в аэродинамической трубе. Аналоговое моделирование основано на аналогии процессов и явлений, имеющих различную физическую природу, но описываемую формально (одними и теми же математическими уравнениями, логическими схемами и т.п.). Типичный пример – изучение механических колебаний с помощью электрической схемы. Другой пример – макет системы кровообращения, на котором стрелочками изображены направления движения крови. По своей сути материальное (предметное) моделирование является экспериментальным. От него принципиальным образом отличается идеальное моделирование, которое основано не на материальной аналогии объекта и модели, а на аналогии идеальной (мыслимой). Идеальное моделирование носит теоретический характер. Важнейшим его видом является математическое моделирование, при котором исследование объекта осуществляется посредством модели, сформулированной на языке математики и с использованием тех или иных математических методов. Классический пример математического моделирования – описание и исследование основных законов механики И. Ньютоном средствами математики. Использование различных моделей и методологии моделирования необходимо для того, чтобы: · понять, как устроен конкретный объект, каковы его структура, основные свойства, законы развития и взаимодействия с окружающим миром; · научиться управлять объектом (процессом) и определить наилучшие способы управления при заданных целях и критериях; · прогнозировать прямые и косвенные последствия реализации разных способов и форм воздействия на объект. Хорошо построенная модель, как правило, дает новые знания об объекте-оригинале. Это, безусловно, очень важное свойство, стимулирующее развитие методов моделирования. Более подробно о моделях и моделировании можно узнать из литературы, например [10]. Далее приведем несколько простейших моделей из экологии и безопасности жизнедеятельности.
Динамика популяций
В современной экологии часто возникает вопрос: как определить численность той или иной популяции через определенное время? Ответ на него не только представляет теоретический, интерес, но и имеет большое практическое значение. Действительно, не зная этого, нельзя правильно планировать эксплуатацию различных возобновляемых природных ресурсов – промысловых рыб, охотничьих угодий и т.п. Может ли в решении этого вопроса помочь математика? Оказывается, да. Рассмотрим здесь некоторые простейшие модели, на которых проиллюстрируем подход к данному вопросу. Пусть некоторая популяция имеет в момент времени t0 биомассу x0. Предположим, что в каждый момент времени скорость увеличения биомассы пропорциональна уже имеющейся биомассе, а возникающие явления конкуренции за источниками питания и самоотравления снижают биомассу пропорционально квадрату наличной биомассы. Если обозначить биомассу в момент времени t через х(t), а изменение ее за время
где α и k – положительные постоянные (параметры). В дифференциальной форме это соотношение имеет вид:
Оно и представляет собой математическую модель процесса изменения биомассы популяций. В экологической литературе уравнение (9.2) часто называют логистическим. Если теперь поставить вопрос о том, какова же будет биомасса в момент времени Т, то на него можно ответить экспериментально – дождаться этого момента и определить биомассу непосредственным измерением (вообще говоря, такое измерение может быть физически неосуществимым). Другой путь – воспользоваться математической моделью, решая задачу Коши для уравнения (9.2) с начальным условием (9.3): x(t0)=x0. (9.3)
Разделяя в уравнении (9.2) переменные, получим уравнение в дифференциалах
Для дальнейшего удобно ввести новую переменную z=αх, (9.5)
тогда (9.4) можно переписать в виде
Возвращаясь к исходному уравнению (9.2), заметим, что если x0 = ln z – ln(k-z)=ln z0- ln (k-z0)+k(t-t0), откуда
значит,
Если x0 >
откуда вытекает, что при x0 < Мы рассмотрели весьма упрощенную ситуацию, так как предполагали, что популяция не взаимодействует ни с какими другими популяциями, учет же этого обстоятельства, конечно, значительно усложняет модель.
Рассмотрим одну из таких моделей. Будем обозначать биомассы двух популяций через х и у соответственно. Предположим, что обе популяции потребляют один и тот же корм, количество которого ограничено, и из-за этого находятся в конкурентной борьбе друг с другом. Французский математик В. Вольтерра в 1926 г. показал, что при таком предположении динамика популяций достаточно хорошо описывается следующей системой дифференциальных уравнений:
где Первые члены правых частей системы (9.10) характеризуют скорость роста популяций при отсутствии ограничивающих факторов. Вторые члены учитывают те изменения в скоростях, которые вызываются ограниченностью корма. Задавая различные значения параметров, с помощью системы (9.10) можно описать взаимодействие двух популяций, одна из которых – хищник, а другая – жертва [36]. В литературе [47] более подробно описаны математические аспекты исследования системы (9.10). Прежде чем исследовать, как будет вести себя система (9.10), заметим, что в любой момент времени t ее состояние полностью описывается значениями х и у: каждому состоянию системы соответствует некоторая точка (х, у) на плоскости хОу, называемой «фазовой плоскостью». Каждой точке фазовой плоскости можно поставить в соответствие вектор (стрелку на рис. 9.2) с координатами, которые являются правыми частями системы, указывающий направление движения в этой точке. Проведя из начальной точки линии, касательные этим векторам, получим траектории, по которым будет происходить движение системы, т. е. решения задачи Коши для системы (9.10) с начальными условиями x(t0)=x0, y(t0)=y0, (х0,у0)Î х0у. (9.11)
Чтобы составить представление о траекториях движения системы, построим линии, на которых х=0 (здесь векторы параллельны оси Оу) и у = 0 (здесь векторы параллельны оси Ох). Для краткости обозначим производную х=0, когда у=0, когда т. е. х = 0 на двух прямых в фазовой плоскости: х=0 и а у=0 также на двух прямых: у=0 и По этим рисункам можно сделать следующие выводы. В обоих случаях имеем три стационарные точки, в которых одновременно х=0 и у=0, а именно: (0,0), (0,
В дальнейших рассмотрениях будем для простоты считать, что k1=k2=k и ε1= ε2= ε. Тогда, деля второе уравнение системы (9.10) на первое, получим
т. е. траекториями являются отрезки прямых, выходящих из начала координат (рис. 9.4). Обе популяции не вымирают и численность их стабилизируется к значениям, которые можно найти как координаты пересечения прямых
Простейшая модель эпидемии
За многие годы существования человечества огромное число людей погибло от разных эпидемий. Для того чтобы уметь бороться с эпидемиями, т. е. своевременно проводить тот или иной комплекс мероприятий (прививки, вакцины, карантин и т.д.), необходимо уметь оценить эффективность каждого такого комплекса и выбрать наиболее оптимальный для данного вида эпидемии (холера, чума, грипп, СПИД и т.д.). Оценка эффективности базируется, как правило, на прогнозе о протекании эпидемии. Отсюда вытекает задача построения модели, которая могла бы служить целям прогноза. Самой простой моделью является описание естественного хода эпидемии без применения каких-либо профилактических мероприятий. Итак, пусть имеется N здоровых людей, и в момент времени t = 0 в эту группу попадает один заболевший человек (источник инфекции). Предположим, что удаления заболевших из группы не происходит и человек становится источником инфекции сразу же, как заразился сам. Обозначим через x(t) число источников инфекции в момент времени t, а через y(t) – число еще не заболевших (часть из них, естественно, может заболеть с течением времени). Очевидно, что х(t) + y(t) = N + 1 в любой момент времени t, причем при t = 0 выполняется условие х(0) = 1. Рассмотрим интервал времени t, t +∆ t, где ∆ t достаточно мало. Естественно, что число больных ∆ х, появившихся за этот интервал, пропорционально ∆ t (∆ x≈ ∆ t). Естественно также предположить, что это число пропорционально числу контактов между больными и здоровыми, т.е. произведению x(t)y(t). Таким образом, ∆x≈ αx(t)y(t)dt, где α – коэффициент пропорциональности. Устремляя ∆ t к нулю из последнего соотношения, получим дифференциальное уравнение
которое вместе с начальным условием х(0)=1 (9.15) определяет функцию x(t). Уравнение (9.14) по виду является логистическим, оно рассмотрено в предыдущем параграфе. Поэтому сразу можно записать решение x(t) задачи Коши (9.14), (9.15) в удобном виде
Итак, число заболевших – функция времени. Проанализируем эту функцию. Из уравнения (9.16) вытекает, что с течением времени число заболевших может только увеличиваться, а все здоровые люди заболеют, так как Интересно выяснить, как меняется скорость увеличения числа больных, т. е. величина
Для решения этого вопроса нужно изучить величину Дифференцируя уравнение (9.17), получаем
Из этого уравнения вытекает, что при t Для сравнения приведем результаты использования более сложных моделей развития гриппозной эпидемии в Москве [22], где население составляет 8,5 млн человек. Это позволит нам также определить численные значения параметров N и α, при которых наша модель более реалистична. Началу эпидемии соответствует число заболевших 79,1 тыс. человек, откуда N = 8,5 млн./79,1 тыс. ≈1100 человек. Пик заболеваемости приходится на 46-й день, т. е. 46
Матричные модели
Матричную модель можно рассматривать как конечно-разностный аналог динамической модели. Один из ранних вариантов матричной модели был разработан Льюисом и Лесли [30] как детерминистская модель, предсказывающая будущую возрастную структуру популяции самок по известной структуре в настоящий момент времени и гипотетическим коэффициентам выживания и плодовитости. Популяцию разбивают на n +1 возрастную группу (т. е. 0, 1, 2,..., п, причем каждая группа состоит из особей одного возраста), так что самая старшая группа, или группа, в которой все доживающие до данного возраста животные вымирают, имеет номер п. Обозначая через xn число особей в каждой возрастной группе, получаем вектор Модель описывается матричным уравнением
которое запишем в развернутом виде:
где величины fi,(i=0, 1,..., n) представляют число самок, производимых самкой i -го возраста, р, (i = 0,1,..., п -1) – вероятность того, что самка i -го возраста доживет до возраста i +1. Покажем, что поведение модели можно предсказать, анализируя некоторые формальные свойства матрицы А. Во-первых, последовательно умножая уравнение (9.19) на матрицу А, легко получить более общие уравнения для численности возрастных групп к моменту времени
Во-вторых, поскольку матрица А квадратная с (n +1) строками и столбцами, она имеет n +1 собственных чисел (с учетом кратности) и (n +1) собственных (и присоединенных) векторов. Элементы А являются либо положительными числами, либо нулями, поэтому наибольшее (по абсолютной величине) собственное число и координаты отвечающего ему собственного вектора положительны и при этом имеют определенный экологический смысл. Проиллюстрируем это на одной из простейших моделей, предложенных Уильямсоном [54]. Исходная популяция имеет вектор, представляющий возрастную структуру а0 = (0,0,1), т. е. популяция состоит из одной самки старшего возраста. Матрица А имеет вид:
По прошествии одного временного интервала имеем
т. е. a 1 = (12, 0, 0) и в популяции уже будет 12 самок младшего возраста. Повторное применение модели дает следующие результаты:
и т.д. Главное собственное число и собственный вектор матрицы А можно найти известными методами, имея
или полагая
определитель которой
Следовательно, главное собственное число λ1 = 2 и собственный вектор в силу (9.23) имеет вид

Нетрудно проверить, что система (9.25) допускает решение
где α0, β0, γ0 – некоторые положительные числа (например, если Тогда уравнение (9.21) примет вид:
Так как
Главное собственное число λ1 дает скорость, с которой возрастает размер популяции (в нашем примере за каждый временной интервал популяция удваивается), а собственный вектор Матричные модели очень удобны для расчета на ЭВМ и находят все более широкое применение, например, для анализа круговорота питательных веществ в экосистемах, в различных стохастических моделях [54] (в марковских моделях и т.д.).
Контрольные задания
1. Показать, что график логистического уравнения имеет единственную точку перегиба. Найти ее и дать биологическую интерпретацию. 2. Рассмотреть систему Вольтерра в случае 3. Построить и исследовать модель эпидемии в городе с 300-тысячным населением. 4. Исходная популяция имеет следующую возрастную структуру a0 = (0,6,12) и матрица Лесли А – следующий вид:
Найти (приближенно) численность популяции через достаточно большое число п лет и ее устойчивую возрастную структуру.
|
||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 671; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.123.240 (0.014 с.) |

 t через
t через 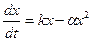 . (9.2)
. (9.2)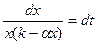 . (9.4)
. (9.4)
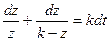 (9.6)
(9.6) (т. е. z0=k), то задача Коши имеет решение x(t)
(т. е. z0=k), то задача Коши имеет решение x(t)  x0 (рис. 9.1). Если x0 <
x0 (рис. 9.1). Если x0 < 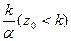 , то уравнение (9.6) интегрируется следующим образом
, то уравнение (9.6) интегрируется следующим образом , (9.7)
, (9.7)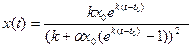 , t > 0 (9.8)
, t > 0 (9.8)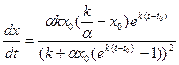 , (9.9)
, (9.9)
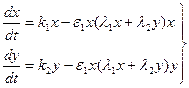 , (9.10)
, (9.10) – определенные положительные числа.
– определенные положительные числа.
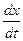 – через х, а
– через х, а 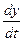 – через у. Имеем
– через у. Имеем ,
, ,
, =
= 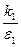 ,
, (рис. 9.2, 9.3).
(рис. 9.2, 9.3). ) и (0,
) и (0, 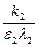 ), которые по известной классификации являются узлами. При этом, если
), которые по известной классификации являются узлами. При этом, если  , а первая стабилизируется, x(t) →
, а первая стабилизируется, x(t) →  , то кроме неустойчивого узла (0,0) имеем линию стационарных точек – отрезок прямой
, то кроме неустойчивого узла (0,0) имеем линию стационарных точек – отрезок прямой 
 =
=  , откуда
, откуда , (9.12)
, (9.12)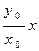 , откуда
, откуда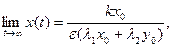
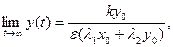 (9.13)
(9.13)
 , t
, t 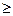 0. (9.16)
0. (9.16) =N+1. Конечно, это грубая модель, не учитывающая естественного иммунитета у здоровых людей к данному заболеванию.
=N+1. Конечно, это грубая модель, не учитывающая естественного иммунитета у здоровых людей к данному заболеванию.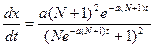 , t
, t  .
.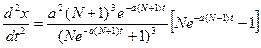 , t
, t  и
и  . Следовательно, скорость возрастания заболевших – функция
. Следовательно, скорость возрастания заболевших – функция  , а затем убывает. Несмотря на грубость модели, этот результат совпадает с экспериментальными данными: в начале эпидемии число заболевших резко возрастает, а впоследствии скорость распространения инфекции снижается.
, а затем убывает. Несмотря на грубость модели, этот результат совпадает с экспериментальными данными: в начале эпидемии число заболевших резко возрастает, а впоследствии скорость распространения инфекции снижается. , откуда
, откуда  . По формуле (9.16) находим число больных
. По формуле (9.16) находим число больных  . По отношению к 1100 чел. это составляет 11%, что согласуется с экспериментальными данными [22], где число больных равно 981 тыс. человек и составляет 11,5%. Конечно, применение соответствующих профилактических мер дает значительный положительный эффект, пик числа больных снижается с 981тыс. до 122 тыс. человек, однако создание соответствующей математической модели – существенно более трудная задача.
. По отношению к 1100 чел. это составляет 11%, что согласуется с экспериментальными данными [22], где число больных равно 981 тыс. человек и составляет 11,5%. Конечно, применение соответствующих профилактических мер дает значительный положительный эффект, пик числа больных снижается с 981тыс. до 122 тыс. человек, однако создание соответствующей математической модели – существенно более трудная задача. представляющий возрастную структуру в момент времени t.
представляющий возрастную структуру в момент времени t.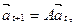 (9.19)
(9.19)
 (9.21)
(9.21)


 (9.22)
(9.22) – систему линейных алгебраических уравнений
– систему линейных алгебраических уравнений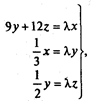

 = (24, 4,1). Остальные собственные числа в силу (9.24) имеют вид λ2 =-1, λ3 =-1. В силу (9.23) собственный вектор
= (24, 4,1). Остальные собственные числа в силу (9.24) имеют вид λ2 =-1, λ3 =-1. В силу (9.23) собственный вектор  имеет вид
имеет вид  (называемого присоединенным), решаем систему уравнений ( A- λ2)
(называемого присоединенным), решаем систему уравнений ( A- λ2)  = (0, - 2, 2) – базисные, т. е.
= (0, - 2, 2) – базисные, т. е.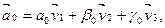 (9.26)
(9.26) = (258, 30, 17), то α0=10, β0=3, γ0=2).
= (258, 30, 17), то α0=10, β0=3, γ0=2). (9.27)
(9.27) → 0, k → ∞, то при t=+k → ∞популяция возрастает по экспоненциальному закону
→ 0, k → ∞, то при t=+k → ∞популяция возрастает по экспоненциальному закону (9.28)
(9.28) .
. . Найти отношения
. Найти отношения  .
.



