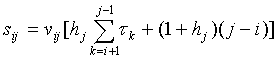Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция: Эволюционное моделирование и генетические алгоритмыСодержание книги
Поиск на нашем сайте Рассматриваются основные понятия и принципы эволюционного моделирования систем, а также генетических алгоритмов - адекватного аппарата его проведения. Цель лекции: ввести в суть проблемы, сформулировать основные положения и принципы, цели эволюционного моделирования и дать общее понятие о генетических алгоритмах и их возможностях в эволюционном моделировании.
Потребность в прогнозе и адекватной оценке последствий осуществляемых человеком мероприятий (особенно негативных) приводит к необходимости моделирования динамики изменения основных параметров системы, динамики взаимодействия открытой системы с его окружением (ресурсы, потенциал, условия, технологии и т.д.), с которым осуществляется обмен ресурсами в условиях враждебных, конкурентных, кооперативных или же безразличных взаимоотношений. Здесь необходимы системный подход, эффективные методы и критерии оценки адекватности моделей, которые направлены не только (не столько) на максимизацию критериев типа "прибыль", "рентабельность", но и на оптимизацию отношений с окружающей средой. Если критерии первого типа важны, например, для кратко- и среднесрочного прогнозирования и тактического администрирования, то второго типа - для средне- и долгосрочного прогноза, для стратегического администрирования. При этом необходимо выделить и изучить достаточно полную и информативную систему параметров исследуемой системы и его окружения, разработать методику введения мер информативности и близости состояний системы. Важно отметить, что при этом некоторые критерии и меры могут часто конфликтовать друг с другом. Многие такие социально-экономические системы можно описывать с единых позиций, средствами и методами единой теории - эволюционной. При эволюционном моделировании процесс моделирования сложной социально-экономической системы сводится к созданию модели его эволюции или к поиску допустимых состояний системы, к процедуре (алгоритму) отслеживания множества допустимых состояний (траекторий). При этом актуализируются такие атрибуты биологической эволюционной динамики (в скобках даны возможные социально-экономические интерпретации этих атрибутов для эволюционного моделирования) как, например:
При исследовании эволюции системы необходима ее декомпозиция на подсистемы с целью обеспечения:
Пусть имеется некоторая система S с N подсистемами. Для каждой i-й подсистемы определим вектор x(i)=(x1(i),x2(i),:,xni(i)) основных параметров (т.е. параметров, без которых нельзя описать и изучить функционирование подсистемы в соответствии с целями и доступными ресурсами системы) и функцию s(i)=s(x(i)), которую назовем функцией активности или просто активностью этой подсистемы. Пример. В бизнес-процессах это понятие близко к понятию деловой активности. Для всей системы определены вектор состояния системы x и активность системы s(x), а также понятие общего потенциала системы. Пример. Потенциал активности может быть определен аналогично биологическому потенциалу популяции, например, с помощью интеграла от активности на задаваемом временном промежутке моделирования. Эти функции отражают интенсивность процессов как в подсистемах, так и в системе в целом. Важными для задач моделирования являются три значения s(i)max, s(i)min, s(i)opt - максимальные, минимальные и оптимальные значения активности i-й подсистемы, а также аналогичные значения для всей системы (smax, smin, sopt). В качестве показателя экономического состояния можно брать также отношение значения этого показателя к его нормированному значению, а для комплексного учета влияния параметров на состояние системы можно использовать аналоги меры информационной близости, например, по К. Шеннону. Если дана открытая экономическая система (процесс), а Н0, Н1 - энтропия системы в начальном и конечном состояниях процесса, то мера информации определяется как разность вида: ΔН=Н0-Н1.Уменьшение ΔН свидетельствует о приближении системы к состоянию статического равновесия (при доступных ресурсах), а увеличение - об удалении. Величина ΔН - количество информации, необходимой для перехода от одного уровня организации системы к другой (при ΔН>0 - более высокой, при ΔН<0 - более низкой организации). Возможен подход и с использованием меры по Н. Моисееву. Пусть дана некоторая управляемая система, о состояниях которой известны лишь некоторые оценки - нижняя smin и верхняя smax. Известна целевая функция управления F(s(t),u(t)), где s(t) - состояние системы в момент времени t, а u(t) - управление из некоторого множества допустимых управлений, причем считаем, что достижимо uopt - некоторое оптимальное управление из пространства U, t0<t<T, smin  [t0;T], s [t0;T], s  [smin;smax]. [smin;smax]. Увеличение Н свидетельствует об успешности управления системой (успешности принятого управляющего решения). Активности подсистем прямо или опосредованно взаимодействуют с помощью системной активности s(x), например, по простой схеме вида
Функции j(i), y(i) должны отражать эволюционируемость системы, в частности, удовлетворять условиям:
 0<T<∞, 0<T<∞,  t: t:  (i)(s; s(i), t)= (i)(s; s(i), t)=  (i)(s; s(i), t+T), (i)(s; s(i), t+T),  (i)(s; s(i), t)= (i)(s; s(i), t)=  (i)(s; s(i), t+T)); (i)(s; s(i), t+T));
 0 0  i=1, 2,..., n) => ( i=1, 2,..., n) => ( (i) (i)  0, 0,  (i) (i)  0); 0);
Взаимные активности
В таких функциях важен параметр Функционирование системы удовлетворяет на каждом временном интервале (t; t+τ) ограничениям вида
При этом отметим, что выполнение для τ>0 одного из двух условий
приводит к разрушению (катастрофе) системы. Пример. Пусть имеется некоторая социально-экономическая среда, которая возобновляет с коэффициентом возобновления
Обозначим
Задача всегда имеет решение x
Чем выше темп Пример. Пусть umax - максимальный уровень синтаксических ошибок в программе Р, u(t) - их оставшееся количество к моменту времени t. Исходя из простейшей эволюционной модели du/dt+λumax=0, u(t0)=u0, можно заключить, что уровень ошибок убывает при λ(c-t0) Отметим, что если ds/dt - общее изменение энтропии системы при воздействии на систему, ds1/dt - изменение энтропии за счет необратимых изменений структуры, потоков внутри системы (рассматриваемой как открытая система), ds2/dt - изменение энтропии за счет усилий по улучшению обстановки (например, экономической, экологической, социальной), то справедливо уравнение И. Пригожина: ds/dt = ds1/dt + ds2/dt.При эволюционном моделировании социально-экономических систем полезно использовать и классические математические модели, и неклассические, в частности, учитывающие пространственную структуру системы (например, клеточные автоматы и фракталы), структуру и иерархию подсистем (например, графы и структуры данных), опыт и интуицию (например, эвристические, экспертные процедуры). Пример. Пусть дана некоторая экологическая система Ω, в которой имеются точки загрязнения (выбросов загрязнителей) xi, i=1, 2,:, n. Каждый загрязнитель xi загрязняет последовательно экосистему в промежутке времени (ti-1; ti], ti=ti-ti-1. Каждый загрязнитель может оказать воздействие на активность другого загрязнителя (например, уменьшить, нейтрализовать или усилить по известному эффекту суммирования воздействия загрязнителей). Силу (меру) такого влияния можно определить через rij, R={rij: i=1,2,:, n-1; j=2,3,:, n}. Структура задаётся графом: вершины - загрязнители, ребра - меры. Найдём подстановку минимизирующую функционал вида:
где F - суммарное загрязнение системы с данной структурой S. Чем быстрее (медленнее) будет произведен учёт загрязнения в точке xi, тем быстрее (медленнее) осуществимы социо-экономические мероприятия по его нейтрализации (усилению воздействия). Чем меньше будет загрязнителей до загрязнителя xi, тем меньше будет загрязнение среды. В качестве меры rij может быть взята мера, учитывающая как время начала воздействия загрязнителей (предшествующих данной xj), так и число, а также интенсивность этих загрязнителей:
где vij - весовой коэффициент, определяющий степень влияния загрязнителя xi на загрязнитель xj (эффект суммирования), hj - весовой коэффициент, учитывающий удельную интенсивность действия загрязнителя xj или интервал τi, в течение которого уменьшается интенсивность (концентрация) загрязнителя. Весовые коэффициенты устанавливаются экспертно или экспериментально. Принцип эволюционного моделирования предполагает необходимость и эффективность использования методов и технологии искусственного интеллекта, в частности, экспертных систем. Основная трудность при построении и использовании эволюционных моделей: в Природе и Познании, в которых эти модели и цели явно или неявно существуют, результаты функционирования системы и достижения цели прослеживаемы часто лишь по прошествии длительного периода времени, хотя в Обществе и Экономике Человек стремится получить результаты в соответствии с целью явно и быстро, с минимальными затратами Ресурсов. Адекватным средством реализации процедур эволюционного моделирования являются генетические алгоритмы. Идея генетических алгоритмов "подсмотрена" у систем живой природы, у систем, эволюция которых развертывается в сложных системах достаточно быстро. Генетический алгоритм - это алгоритм, основанный на имитации генетических процедур развития популяции в соответствии с принципами эволюционной динамики, приведенными выше. Часто используется для решения задач оптимизации (многокритериальной), поиска, управления. Данные алгоритмы адаптивны, развивают решения, развиваются сами. Особенность этих алгоритмов - их успешное использование при решении NP-сложных проблем (проблем, для которых невозможно построить алгоритм с полиномиально возрастающей алгоритмической сложностью). Пример. Рассмотрим задачу безусловной целочисленной оптимизации (размещения): найти максимум f(i), i - набор из n нулей и единиц, например, при n=5, i=(1,0,0,1,0). Это очень сложная комбинаторная задача для обычных, "негенетических" алгоритмов. Генетический алгоритм может быть построен следующей укрупненной процедурой:
кц Указанные процедуры определяются с использованием аналогичных процедур живой природы (на том уровне знаний о них, что мы имеем). Например, процедура СЕЛЕКЦИЯ может из случайных элементов популяции выбирать элемент с наибольшим значением f(i). Процедура СКРЕЩИВАНИЕ (кроссовер) может по векторам i1, i2 строить вектор i, присваивая с вероятностью 0,5 соответствующую координату каждого из этих векторов-родителей. Это самая простая процедура. Используют и более сложные процедуры, реализующие более полные аналоги генетических механизмов. Процедура МУТАЦИЯ также может быть простой или сложной. Например, простая процедура с задаваемой вероятностью для каждого вектора меняет его координаты на противоположные (0 на 1, и наоборот). Процедура ОБНОВИТЬ заключается в обновлении всех элементов популяции в соответствии с указанными процедурами. Пример. Работу банка можно моделировать на основе генетических алгоритмов. С их помощью можно выбирать оптимальные банковские проценты (вкладов, кредитов) некоторого банка в условиях конкуренции с тем, чтобы привлечь больше клиентов (средств). Тот банк, который сможет привлечь больше вкладов, клиентов и средств, и выработает более привлекательную стратегию поведения (эволюции) - тот и выживет в условиях естественного отбора. Филиалы такого банка (гены) будут лучше приспосабливаться и укрепляться в экономической нише, а, возможно, и увеличиваться с каждым новым поколением. Каждый филиал банка (индивид популяции) может быть оценен мерой его приспособленности. В основе таких мер могут лежать различные критерии, например, аналог экономического потенциала - рейтинг надежности банка или соотношение привлеченных и собственных средств банка. Такая оценка эквивалентна оценке того, насколько эффективен организм при конкуренции за ресурсы, т.е. его выживаемости, биологическому потенциалу. При этом особи (филиалы) могут приводить к появлению потомства (новых банков, получаемых в результате слияния или распада), сочетающего те или иные (экономические) характеристики родителей. Например, если один банк имел качественную политику кредитования, а другой - эффективную инвестиционную политику, то новый банк может приобрести и то, и другое. Наименее приспособленные особи (филиалы) совсем могут исчезнуть в результате эволюции. Таким образом, отрабатывается генетическая процедура воспроизводства новых банков (нового поколения), более приспособленных и способных к выживанию в процессе эволюции банковской системы. Эта политика со временем пронизывает всю банковскую "популяцию", обеспечивая достижение цели - появления эффективно работающей, надежной и устойчивой банковской системы. Приведем соответствующий генетический алгоритм (укрупненный и упрощенный): алг ГЕНЕТИЧЕСКИЙ_АЛГОРИТМ_БАНКОВСКОЙ_СИСТЕМЫ ввод Начальная структура банка (начальная популяция); СТРУКТУРА | процедура оценки структуры по приспособлению Стоп:=0 | флаг для завершения эволюционного процесса нц пока (Стоп=0) СЕЛЕКЦИЯ | процедура генетического отбора нового поколения нц пока (МЕРА) | цикл воспроизводства с критерием МЕРА | мерой эффективности банковской системы РОДИТЕЛИ | процедура выбора двух структур (филиалов) | объединяемых (скрещиваемых) на новом шаге ОБЪЕДИНЕНИЕ | процедура образования (объединения) | нового банка (филиала) ОЦЕНКА | процедура оценки устойчивости нового банка, | образования (рейтинга, устойчивости) ВКЛЮЧЕНИЕ | процедура включения (не включения) в новое | поколение (в банковскую систему) кц МУТАЦИЯ | процедура эволюции (мутации) нового поколения если (ПРОЦЕСС) | проверка функционала завершаемости эволюции то Стоп:=1 кцкон.Мы не конкретизируем структуру процедур СЕЛЕКЦИЯ, МЕРА, РОДИТЕЛИ, ОБЪЕДИНЕНИЕ, ОЦЕНКА, ВКЛЮЧЕНИЕ, МУТАЦИЯ, ПРОЦЕСС, хотя даже на интуитивном уровне ясно, что в этом алгоритме они играют решающую роль для эволюционного процесса. Не менее важен и правильный (эффективный) выбор структуры, а также представления (описания) этой структуры. Часто ее выбирают по аналогии со структурой хромосом, например, в виде битовых строк. Каждая строка (хромосома) представляет собой конкатенацию ряда подстрок (генная комбинация). Гены располагаются в различных позициях строки (локусах хромосомы). Они могут принимать некоторые значения (аллели), например, для битового представления - 0 и 1. Структура данных в генетическом алгоритме (генотип) отражает генетическую модель особи. Окружающая среда, окружение определяется вектором в пространстве параметров и соответствует термину "фенотип". Мера качества (процедура МЕРА) структуры часто определяется целевой функцией (приспособленности). Для каждого нового поколения генетический алгоритм осуществляет отбор пропорционально приспособленности (процедура ОТБОР), модификацию (процедуры РОДИТЕЛИ, ОБЪЕДИНЕНИЕ, ВКЛЮЧЕНИЕ) и мутацию (процедура МУТАЦИЯ). Например, в процедуре ОТБОР каждой структуре ставится в соответствие отношение ее приспособленности к суммарной приспособленности популяции и затем происходит отбор (с замещением) всех особей для дальнейшей генетической обработки в соответствии с этой величиной. Размер отбираемой комбинации можно брать пропорциональным приспосабливаемости, и поэтому особи (кластеры) с более высокой приспособленностью с большей вероятностью будут чаще выбираться, чем особи с низкой приспособленностью. После отбора выбранные особи подвергаются кроссоверу (рекомбинации), т.е. разбиваются на пары. Для каждой пары может применяться кроссовер. Неизмененные особи переходят к стадии мутации. Если кроссовер происходит, полученные потомки заменяют собой родителей и переходят к мутации. Хотя генетические алгоритмы и могут быть использованы для решения задач, которые, видимо, нельзя решать другими методами, они не гарантируют нахождение оптимального решения (по крайней мере, - за приемлемое время; полиномиальные оценки здесь часто неприменимы). Здесь более уместны критерии типа "достаточно хорошо и достаточно быстро". Главное же преимущество в другом: они позволяют решать сложные задачи, для которых не разработаны пока устойчивые и приемлемые методы, особенно на этапе формализации и структурирования системы, в когнитивных системах. Генетические алгоритмы эффективны в комбинации с другими классическими алгоритмами, эвристическими процедурами, а также в тех случаях, когда о множестве решений есть некоторая дополнительная информация, позволяющая настраивать параметры модели, корректировать критерии отбора, эволюции. Вопросы для самоконтроля
Задачи и упражнения
|
||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 471; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.01 с.) |



 s
s 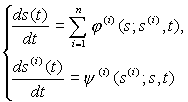
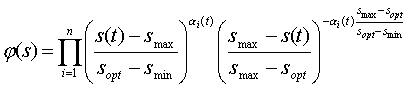
 i, отражающий степень саморегуляции, адаптации системы. Как правило, его нужно идентифицировать.
i, отражающий степень саморегуляции, адаптации системы. Как правило, его нужно идентифицировать.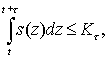
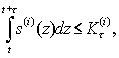
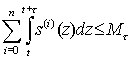
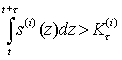
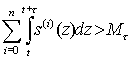
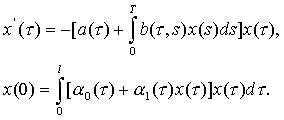
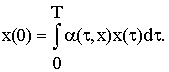
 0. Тогда эволюционный потенциал системы можно определить как величину:
0. Тогда эволюционный потенциал системы можно определить как величину: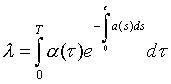
 -1 (t0<c<T) по закону: u(t) = u0(1+ λ(c-t))/(1+λ(c-t0)). Если задать дополнительно u(t*)=u*, (umax - неизвестная величина, t*
-1 (t0<c<T) по закону: u(t) = u0(1+ λ(c-t))/(1+λ(c-t0)). Если задать дополнительно u(t*)=u*, (umax - неизвестная величина, t*