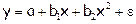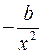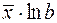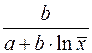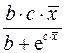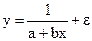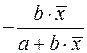Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
И 19) Идентификация модели системы эконометрических уравненийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Вопросы
Определение эконометрики Эконометрика — наука, изучающая количественные и качественные экономические взаимосвязи с помощью математических и статистических методов и моделей. Эконометрика — наука, позволяющая качественным социальным процессам присвоить количественные характеристики и дать их экономическую интерпретацию. Эта наука возникла в результате взаимодействия и объединения трех компонент: экономической теории, статистических и экономических методов. Термин "эконометрика" впервые был введен бухгалтером П. Цьемой (Австро-Венгрия, 1910 г.). Термин «эконометрика» состоит из двух частей: «эконо» — от «экономика» и «метрика» — от «измерение». Современное определение предмета эконометрики было выработано в уставе Эконометрического общества, которое главными целями назвало использование статистики и математики для развития экономической теории. Теоретическая эконометрика рассматривает статистические свойства оценок и испытаний, в то время как прикладная эконометрика занимается применением эконометрических методов для оценки экономических теорий. Эконометрика дает инструментарий для экономических измерений, а также методологию оценки параметров моделей микро- и макроэкономики. Кроме того, эконометрика активно используется для прогнозирования экономических процессов как в масштабах экономики в целом, так и на уровне отдельных предприятий. При этом эконометрика является частью экономической теории, наряду с макро- и микроэкономикой.
Эконометрика входит в обширное семейство дисциплин, посвященных измерениям и применению статистических методов в различных областях науки и практики. К этому семейству относятся, в частности, биометрия, технометрика, наукометрия, психометрия, хемометрия, квалиметрия. Особняком стоит социометрия — этот термин закрепился за статистическими методами анализа взаимоотношений в малых группах, то есть за небольшой частью такой дисциплины, как статистический анализ в социологии.
Объект изучения эконометрики - экономико-математические модели, которые строятся с учетом случайных факторов. Такие модели называются эконометрическими моделями.
Основные задачами эконометрики: - выявление связей между количественными характеристиками экономических объектов в целях построения математических правил прогноза - определить значения всех числовых параметров, входящих в модель и обеспечить соответствие ее реальному поведению объекта - получение наилучших оценок параметров экономико-математических моделей, конструируемых в прикладных целях; - проверка теоретико-экономических положений и выводов на фактическом (эмпирическом) материале; - создание универсальных и специальных методов для обнаружения статистических закономерностей в экономике.
Основная цель эконометрики дать исследователям инструмент для прогнозирования поведения экономического объекта в различных ситуациях и на базе прогнозирования решать практические задачи по оптимальному управлению объектом, выбору стратегии поведения на рынке и т.п.
Измерения в экономике Теория измерений является одной из составных частей эконометрики. Она входит в состав статистики объектов нечисловой природы. Измерение понимается по-разному. Прежде всего, признаками измерения называют получение, сравнение и упорядочение информации. Это определение исходит из того, что измерение предполагает выделение некоторого свойства, по которому производится сравнение объектов в определенном отношении. Так определяется измерение в широком смысле. Другое понимание измерения исходит из числового выражения результата, т.е. измерение трактуется как операция, в результате которой получается численное значение величины, причем числа должны соответствовать наблюдаемым свойствам, фактам, качествам, законам науки и т. д. Третий подход к измерению связан с обязательным наличием единицы измерения (эталона). Это определение измерения в узком смысле. Первый, низший, уровень измерения предполагает сравнение объектов по наличию или по отсутствию исследуемого свойства. На этом уровне измерения используются термины «номинация», «классификация», «нумерация». Второй уровень предполагает сравнение объектов по интенсивности проявляемых свойств. На этом уровне используются термины «шкалирование», «топология», «упорядочение». Третий, высший, уровень измерения предполагает сравнение объектов с эталоном (в контексте физического измерения). На этом уровне используются термины «измерение», «квантификация». Все понятия измерения могут быть объединены на базе определения шкалы измерения. Тип шкалы определяется допустимым преобразованием. Допустимое преобразование – это преобразование, при котором сохраняются неизменными отношения между элементами системы. Для определения любой шкалы измерения необходимо дать название объекта, отождествить объект с некоторым свойством или группой свойств. Если это требование оказывается единственным, то шкала называется шкалой наименований или номинальной шкалой. Измерением в номинальной шкале можно считать любую классификацию, по которой класс получает числовое наименование. Шкала, в которой порядок элементов по уровню проявления некоторого свойства существенен, а количественное выражение различия несущественно или плохо осуществимо, называется порядковой, или ранговой. Шкала порядка, или ординальная шкала, допускает операции «равенство-неравенство», «больше-меньше». Порядковые данные возникают, например, при определении предпочтений избирателей и рейтинга того или иного кандидата, экспертиз качества, при оценке силы землетрясений, измерении полезности, оценке уровня интеллекта, а также при определении потенциала человеческого развития и т. д. Кроме номинальной и порядковой шкал для определения измерения используются интервальные шкалы. Измерения в интервальных шкалах в известном смысле более совершенны, чем в порядковых. Применение этих шкал дает возможность не только упорядочить объекты по количеству свойства, но и сравнить между собой разности количеств. Таким образом, мы получаем возможность не только указать категорию, к которой относится объект по данному признаку, установить его место в ранжированном ряде, но и описать его отличие от других объектов, рассчитав разность (интервал) между соответствующими позициями на шкале. Примерами интервальных шкал могут служить измерения большинства экономических параметров (производительность труда, себестоимость, рентабельность, ликвидность и т. д.). Формально интервальная шкала определяется как единственная до линейного преобразования шкала вида y=kx+b, где a и b ‑ числа, для которых определены операции сложения и умножения, соответственно a>0, b¹0. Параметр a называется масштабом, а параметр b – началом отсчета. По шкале отношений начало отсчета нельзя выбрать произвольно и параметр b=0. Можно сказать, что шкала отношений – это интервальная шкала с естественным началом. Шкала отношений – это единственная с точностью до линейных преобразований шкала вида y=ax при a¹0, где a ‑ масштаб. Пропорциональная шкала допускает операции «равенство-неравенство интервалов», «меньше-больше», операцию деления, на основе которой устанавливается равенство-неравенство отношений. Если в интервальной шкале масштаб зафиксирован, то измерение происходит в шкале разностей. Шкала разностей допускает операции «равенство-неравенство», «больше-меньше», «равенство-неравенство интервалов» и операцию вычитания, на основе которой устанавливается величина интервала в фиксированном масштабе. К шкале разностей относятся логарифмические шкалы, а также процентные и аналогичные им шкалы измерений, задающие безразмерные величины. Например, указание года рождения – это представление возраста в шкале разностей. Шкала разностей существенна с точностью до линейного преобразования вида y=x+a, где b¹0. Такое преобразование называется сдвигом. Если зафиксированы масштаб и точка отсчета, то переменная изменяется в абсолютной шкале с точностью до тождественного преобразования вида y=x. Эта шкала допускает все операции. В абсолютной шкале изменяются, например, вероятность, число работников и т. д. Таким образом, в определении шкал участвуют понятия равенства, порядка, дистанции между пунктами шкалы (интервалы), начала отсчета и единицы измерения. В зависимости от наличия или отсутствия этих элементов возникают различные типы шкал. Представления о точности измерений могут быть получены из анализа погрешностей. Точность измерения – это его адекватность. Универсальные критерии точности отсутствуют. Критерий точности каждого вида измерения определяется в соответствии с целями этого измерения. Погрешности измерения не сводятся к арифметическим погрешностям. Поиск измерителя исследуемого признака может происходить в трех направлениях: - выбор показателя, который может служить индикатором исследуемого признака (латенты); - определение функциональной зависимости значения исследуемого признака от значений наблюдаемых признаков; - построение системы признаков, характеризующей исследуемый признак. Множественная регрессия. Требования, предъявляемые к факторам, включенным в модель. При рассмотрении экономических процессов чаще всего приходится обращаться к моделям, содержащим более одного фактора-признака. Таким образом, следует включить в модель не один фактор, а несколько, т.е. построить уравнение множественной регрессии. Уравнение множественной регрессии имеет вид: y=f(x1,x2,…,xk) Простейшая функция для построения множественной регрессионной модели – линейная: y = a + b1x1 + b2x2 +…+ bkxk +ε. Множественная регрессия широко используется в решении проблем спроса, доходности акций, при изучении функции издержек производства, в макроэкономических расчетах и целого ряда других вопросов эконометрики. В настоящее время множественная регрессия – один из наиболее распространенных методов в эконометрике. Основная цель – построить модель с большим числом факторов, определив при этом влияние каждого из них в отдельности, а также их совокупное воздействие на моделируемый показатель. Требования, предъявляемые к факторам, для включения в модель: 1. Они должны быть количественно измеримы. Если необходимо включить в модель качественный фактор, не имеющий количественного измерения, то ему нужно придать количественную определенность. 2. Факторы не должны быть интеркоррелированы и тем более находиться в точной функциональной связи. Включение в модель факторов с высокой интеркорреляцией, когда Ryx1<Rx1x2 для зависимости y = a + b1x1 + b2x2 + ε может привести к нежелательным последствиям - система нормальных уравнений может оказаться плохо обусловленной и повлечь за собой неустойчивость и ненадежность оценок коэффициентов регрессии. Если между факторами существует высокая корреляция, то нельзя определить их изолированное влияние на результативный показатель и параметры уравнения регрессии оказываются неинтерпретируемыми. 3. Включаемые во множественную регрессию факторы должны объяснить вариацию независимой переменной. Если строится модель с набором р факторов, то для нее рассчитывается показатель детерминации R2, который фиксирует долю объясненной вариации результативного признака за счет рассматриваемых в регрессии р факторов. Влияние других, не учтенных в модели факторов, оценивается как 1— R2 с соответствующей остаточной дисперсией S2. При дополнительном включении в регрессию р+1 фактора коэффициент детерминации должен возрастать, а остаточная дисперсия уменьшаться: R2p+1 Если же этого не происходит и данные показатели практически мало отличаются друг от друга, то включаемый в анализ фактор xp+1 не улучшает модель и практически является лишним фактором. Отбор факторов обычно осуществляется в две стадии: - отбираются факторы, исходя из сущности проблемы - на основе матрицы показателей корреляции определяют t-статистики для параметров регрессии.
Коэффициенты интеркорреляции (т.е. корреляции между объясняющими переменными) позволяют исключать из модели дублирующие факторы. Считается, что две переменные явно коллинеарны, т.е. находятся между собой в линейной зависимости, если rxixj³0,7. Поскольку одним из условий построения уравнения множественной регрессии является независимость действия факторов, т.е. Rxixj=0, то коллинеарность факторов нарушает это условие. Если факторы явно коллинеарны, то они дублируют друг друга и один из них рекомендуется исключить из регрессии. Предпочтение при этом отдается тому фактору, который при достаточно тесной связи с результатом имеет наименьшую тесноту связи с другими факторами.
Основой измерения показателей тесноты связей является матрица парных коэффициентов корреляции
По этой матрице можно судить о тесноте связи факторов с результативным признаком и между собой. Хотя все эти показатели относятся к парным связям, все же матрицу можно использовать для предварительного отбора факторов для включения в уравнение регрессии. Не рекомендуется включать в уравнение факторы слабо связанные с результативными признаками, но тесно связанные с другими факторами. По величине парных коэффициентов корреляции обнаруживается лишь явная коллинеарность факторов. Наибольшие трудности в использовании аппарата множественной регрессии возникают при наличии мультиколлинеарности факторов, когда более чем два фактора связаны между собой линейной зависимостью, т.е. имеет место совокупное воздействие факторов друг на друга. Наличие мультиколлинеарности факторов может означать, что некоторые факторы будут всегда действовать в унисон. Включение в модель мультиколлинеарных факторов нежелательно в силу следующих последствий: - затрудняется интерпретация параметров множественной регрессии как характеристик действия факторов в «чистом» виде, ибо факторы коррелированны; параметры линейной регрессии теряют экономический смысл; - оценки параметров ненадежны, обнаруживают большие стандартные ошибки и меняются с изменением объема наблюдений (не только по величине, но и по знаку), что делает модель непригодной для анализа и прогнозирования. Для оценки мультиколлинеарности факторов может использоваться определитель матрицы парных коэффициентов корреляции между факторами.
Чем det|R| ближе к нулю, тем сильнее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии. Фиктивные переменные До сих пор в качестве факторов рассматривались экономические переменные, принимающие количественные значения в некотором интервале. Вместе с тем может оказаться необходимым включить в модель фактор, имеющий два или более качественных уровней. Это могут быть разного рода атрибутивные признаки, такие, например, как профессия, пол, образование, климатические условия, принадлежность к определенному региону. Чтобы ввести такие переменные в регрессионную модель, им должны быть присвоены те или иные цифровые метки, т.е. качественные переменные преобразованы в количественные. Такого вида сконструированные переменные в эконометрике принято называть фиктивными переменными. Рассмотрим применение фиктивных переменных для функции спроса. Предположим, что по группе лиц мужского и женского пола изучается линейная зависимость потребления кофе от цены. В общем виде для совокупности обследуемых уравнение регрессии имеет вид: y=a+bx+e, где y – количество потребляемого кофе; x– цена. Аналогичные уравнения могут быть найдены отдельно для лиц мужского пола: y1=a1+b1x1+e1 и женского пола: y2=a2+b2x2+e2. Различия в потреблении кофе проявятся в различии средних y=a1z1+a2z2+bx+e, где z1и z2 – фиктивные переменные, принимающие значения:
В общем уравнении регрессии зависимая переменная y рассматривается как функция не только цены yx, но и пола (z1,z2). Переменная z рассматривается как дихотомическая переменная, принимающая всего два значения: 1 и 0. При этом когда z1=1, то z2=0, и наоборот. Для лиц мужского пола, когда z1=1 и z2=0, объединенное уравнение регрессии составит: Однако при введении двух фиктивных переменных z1 и z2 в модель y=a1z1+a2z2+bx+e применение МНК для оценивания параметров a1 и a2 приведет к вырожденной матрице исходных данных, а следовательно, и к невозможности получения их оценок. Объясняется это тем, что при использовании МНК в данном уравнении появляется свободный член, т.е. уравнение примет вид y=A+a1z1+a2z2+bx+e. Предполагая при параметре A независимую переменную, равную 1, имеем следующую матрицу исходных данных:
В рассматриваемой матрице существует линейная зависимость между первым, вторым и третьим столбцами: первый равен сумме второго и третьего столбцов. Поэтому матрица исходных факторов вырождена. Выходом из создавшегося затруднения может явиться переход к уравнениям y=A+A1z1+bx+e или y=A+A2z2+bx+e, т.е. каждое уравнение включает только одну фиктивную переменную z1 или z2. Предположим, что определено уравнение y=A+A1z1+bx+e, где z1 принимает значения 1 для мужчин и 0 для женщин. Теоретические значения размера потребления кофе для мужчин будут получены из уравнения
Для женщин соответствующие значения получим из уравнения
Сопоставляя эти результаты, видим, что различия в уровне потребления мужчин и женщин состоят в различии свободных членов данных уравнений: A– для женщин и A+A1 – для мужчин. Теперь качественный фактор принимает только два состояния, которым соответствуют значения 1 и 0. Если же число градаций качественного признака-фактора превышает два, то в модель вводится несколько фиктивных переменных, число которых должно быть меньше числа качественных градаций. Только при соблюдении этого положения матрица исходных фиктивных переменных не будет линейно зависима и возможна оценка параметров модели. Мы рассмотрели модели с фиктивными переменными, в которых последние выступают факторами. Может возникнуть необходимость построить модель, в которой дихотомический признак, т.е. признак, который может принимать только два значения, играет роль результата. Подобного вида модели применяются, например, при обработке данных социологических опросов. В качестве зависимой переменной y рассматриваются ответы на вопросы, данные в альтернативной форме: «да» или «нет». Поэтому зависимая переменная имеет два значения: 1, когда имеет место ответ «да», и 0 – во всех остальных случаях. Модель такой зависимой переменной имеет вид: y=a=b1x1+…+bmxm+e Модель является вероятностной линейной моделью. В ней y принимает значения 1 и 0, которым соответствуют вероятности p и 1-p. Поэтому при решении модели находят оценку условной вероятности события y при фиксированных значениях x. Для оценки параметров линейно-вероятностной модели применяются методы Logit-, Probit- и Tobit-анализа. Такого рода модели используют при работе с неколичественными переменными. Как правило, это модели выбора из заданного набора альтернатив. Зависимая переменная y представлена дискретными значениями (набор альтернатив), объясняющие переменные xi – характеристики альтернатив (время, цена), zj – характеристики индивидов (возраст, доход, уровень образования). Модель такого рода позволяет предсказать долю индивидов в генеральной совокупности, которые выбирают данную альтернативу. Среди моделей с фиктивными переменными наибольшими прогностическими возможностями обладают модели, в которых зависимая переменная y рассматривается как функция ряда экономических факторов xi и фиктивных переменных zj. Последние обычно отражают различия в формировании результативного признака по отдельным группам единиц совокупности, т.е. в результате неоднородной структуры пространственного или временного характера.
Коэффициент эластичности Коэффициент эластичности показывает относительное изменение исследуемого экономического показателя под действием единичного относительного изменения экономического фактора, от которого он зависит при неизменных остальных влияющих на него факторов. Коэффициент эластичности показывает, на сколько процентов измениться в среднем результат, если фактор изменится на 1%. Формула для расчета коэффициента эластичности имеет вид: Обычно рассчитывается средний коэффициент эластичности: Формулы для расчета средних коэффициентов эластичности для наиболее часто используемых типов уравнений регрессии:
Несмотря на широкое применения в эконометрике коэффициентов эластичности, возможны случаи, когда расчет коэффициента эластичности не имеет смысла. Это происходит тогда, когда для рассматриваемых признаков бессмысленно определение изменения в процентах.
Вопросы
Определение эконометрики Эконометрика — наука, изучающая количественные и качественные экономические взаимосвязи с помощью математических и статистических методов и моделей. Эконометрика — наука, позволяющая качественным социальным процессам присвоить количественные характеристики и дать их экономическую интерпретацию. Эта наука возникла в результате взаимодействия и объединения трех компонент: экономической теории, статистических и экономических методов. Термин "эконометрика" впервые был введен бухгалтером П. Цьемой (Австро-Венгрия, 1910 г.). Термин «эконометрика» состоит из двух частей: «эконо» — от «экономика» и «метрика» — от «измерение». Современное определение предмета эконометрики было выработано в уставе Эконометрического общества, которое главными целями назвало использование статистики и математики для развития экономической теории. Теоретическая эконометрика рассматривает статистические свойства оценок и испытаний, в то время как прикладная эконометрика занимается применением эконометрических методов для оценки экономических теорий. Эконометрика дает инструментарий для экономических измерений, а также методологию оценки параметров моделей микро- и макроэкономики. Кроме того, эконометрика активно используется для прогнозирования экономических процессов как в масштабах экономики в целом, так и на уровне отдельных предприятий. При этом эконометрика является частью экономической теории, наряду с макро- и микроэкономикой.
Эконометрика входит в обширное семейство дисциплин, посвященных измерениям и применению статистических методов в различных областях науки и практики. К этому семейству относятся, в частности, биометрия, технометрика, наукометрия, психометрия, хемометрия, квалиметрия. Особняком стоит социометрия — этот термин закрепился за статистическими методами анализа взаимоотношений в малых группах, то есть за небольшой частью такой дисциплины, как статистический анализ в социологии.
Объект изучения эконометрики - экономико-математические модели, которые строятся с учетом случайных факторов. Такие модели называются эконометрическими моделями.
Основные задачами эконометрики: - выявление связей между количественными характеристиками экономических объектов в целях построения математических правил прогноза - определить значения всех числовых параметров, входящих в модель и обеспечить соответствие ее реальному поведению объекта - получение наилучших оценок параметров экономико-математических моделей, конструируемых в прикладных целях; - проверка теоретико-экономических положений и выводов на фактическом (эмпирическом) материале; - создание универсальных и специальных методов для обнаружения статистических закономерностей в экономике.
Основная цель эконометрики дать исследователям инструмент для прогнозирования поведения экономического объекта в различных ситуациях и на базе прогнозирования решать практические задачи по оптимальному управлению объектом, выбору стратегии поведения на рынке и т.п.
и 19) Идентификация модели системы эконометрических уравнений При переходе от приведенной формы модели к структурной эконометрист сталкивается с проблемой идентификации. Идентификация – это единственность соответствия между приведенной и структурной формами модели. Структурная модель
в полном виде содержит m×(m+n-1) параметров, а приведенная форма модели в полном виде содержит (m×n) параметров. Т.е. в полном виде структурная модель содержит большее число параметров, чем приведенная форма модели. Соответственно m×(m+n-1) параметров структурной модели не могут быть однозначно определены из (m×n) параметров приведенной формы модели.
Чтобы получить единственно возможное решение для структурной модели, необходимо предположить, что некоторые из структурных коэффициентов модели ввиду слабой взаимосвязи признаков с эндогенной переменной из левой части системы равны нулю. Тем самым уменьшится число структурных коэффициентов модели. Уменьшение числа структурных коэффициентов модели возможно и другим путем: например, путем приравнивания некоторых коэффициентов друг к другу, т.е. путем предположений, что их воздействие на формируемую эндогенную переменную одинаково. С позиции идентифицируемости структурные модели можно подразделить на три вида: 1) идентифицируемые; 2) неидентифицируемые; 3) сверхидентифицируемые.
Модель идентифицируема, если все структурные ее коэффициенты определяются однозначно, единственным образом по коэффициентам приведенной формы модели, т. е. если число параметров структурной модели равно числу параметров приведенной формы модели. В этом случае структурные коэффициенты модели оцениваются через параметры приведенной формы модели и модель идентифицируема. Модель неидентифицируема, если число приведенных коэффициентов меньше числа структурных коэффициентов, и в результате структурные коэффициенты не могут быть оценены через коэффициенты приведенной формы модели. Модель сверхидентифицируема, если число приведенных коэффициентов больше числа структурных коэффициентов. В этом случае на основе коэффициентов приведенной формы можно получить два или более значений одного структурного коэффициента. В этой модели число структурных коэффициентов меньше числа коэффициентов приведенной формы. Сверхидентифицируемая модель в отличие от неидентифицируемой модели практически решаема, но требует для этого специальных методов исчисления параметров.
Структурная модель всегда представляет собой систему совместных уравнений, каждое из которых требуется проверять на идентификацию. Если хотя бы одно из уравнений системы неидентифицируемо, то и вся модель считается неидентифицируемой. Модель считается идентифицируемой, если каждое уравнение системы идентифицируемо. Сверхидентифицируемая модель содержит хотя бы одно сверхидентифицируемое уравнение.
Выполнение условия идентифицируемости модели проверяется для каждого уравнения системы. Если обозначить число эндогенных переменных в i-м уравнении системы через H, а число экзогенных (предопределенных) переменных, которые содержатся в системе, но не входят в данное уравнение, — через D, то необходимое условие идентифицируемости модели может быть записано в виде: D+1<H уравнение неидентифицируемо D+1=H уравнение идентифицируемо D+1>H уравнение сверхидентифицируемо
Для оценки параметров структурной модели система должна быть идентифицируема или сверхидентифицируема.
Более точно условия идентификации определяются, если накладывать ограничения на коэффициенты матриц параметров структурной модели. Уравнение идентифицируемо, если по отсутствующим в нем переменным (эндогенным и экзогенным) можно из коэффициентов при них в других уравнениях системы получить матрицу, определитель которой не равен нулю, а ранг матрицы не меньше, чем число эндогенных переменных в системе без одного. Целесообразность проверки условия идентификации модели через определитель матрицы коэффициентов, отсутствующих в данном уравнении, но присутствующих в других, объясняется тем, что возможна ситуация, когда для каждого уравнения системы выполнено необходимое условие идентифицируемости модели, а о
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 680; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.018 с.) |

 R2p и S2p+1
R2p и S2p+1  S2p.
S2p.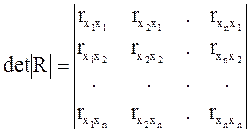
 и
и 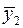 . Вместе с тем сила влияния x на x может быть одинаковой, т.е. b»b1»b2. В этом случае возможно построение общего уравнения регрессии с включением в него фактора «пол» в виде фиктивной переменной. Объединяя уравнения y1 и y2 и, вводя фиктивные переменные, можно прийти к следующему выражению:
. Вместе с тем сила влияния x на x может быть одинаковой, т.е. b»b1»b2. В этом случае возможно построение общего уравнения регрессии с включением в него фактора «пол» в виде фиктивной переменной. Объединяя уравнения y1 и y2 и, вводя фиктивные переменные, можно прийти к следующему выражению: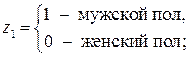
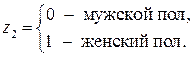
 , а для лиц женского пола, когда z1=0 и z2=1:
, а для лиц женского пола, когда z1=0 и z2=1:  . Иными словами, различия в потреблении для лиц мужского и женского пола вызваны различиями свободных членов уравнения регрессии: a1¹a2. Параметр b является общим для всей совокупности лиц, как для мужчин, так и для женщин.
. Иными словами, различия в потреблении для лиц мужского и женского пола вызваны различиями свободных членов уравнения регрессии: a1¹a2. Параметр b является общим для всей совокупности лиц, как для мужчин, так и для женщин. .
. .
. .
.
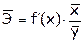 .
.