
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Конспект лекций по моделированию системСодержание книги Поиск на нашем сайте
Конспект лекций по моделированию систем
Выполнил студент: группы ИТ-424 Вафина И. А. Преподаватель: Замыслов В.Е.
2007 г. Содержание: § 1. Основные понятия. 3 § 2. Классификация моделей. 5 § 3. Этапы составления и исследования моделей. 6 § 4. Имитационное моделирование. 8 § 5.Элементы теории вероятности. 10 Способы вычисления вероятности. 10 § 6.Примеры основных случайных величин и их характеристик. 14 § 7.Построение датчика псевдослучайных чисел. 16 § 7.1 Датчики для равномерного закона распределения. 16 § 7.2 Построение датчика псевдослучайных чисел для любого закона распределения 16 § 7.3 Построение датчика по показательному закону распределения. 17 § 7.4 Построение датчика с помощью таблицы квантилей. 18 § 8. Потоки случайных событий. Пуассоновский поток. 19 § 9.Связь потока Пуассона с показательным законом распределения. 21 § 11. Моделирование работы конечного автомата. 24 §12. Моделирование работы системы массового обслуживания. 27 § 13. Двумерные случайные величины и их законы распределения. 34 § 14.Понятие зависимых и независимых случайных величин. 36 §15 Условное математическое ожидание линии регрессии. 38 §16 Числовые характеристики двумерных случайных величин. 39 Корреляционный момент. 39 §17 Виды зависимости между случайными величинами. 42 §18 Нахождение на практике линейной регрессии. 45
Понятия модели и моделирования. Для определения этих понятий необходимо рассмотреть следующие задачи: Задача №1 По рельсу катиться колесо, нужно определить какие силы действуют на колесо
Fупр=-k1·y(t) жесткость пружины- закон Гука Fс=-k2·y’(t) 2 закон Ньютона my’(t)= k1·y(t)-k2·y’(t)-mg+Fвын my’’(t)+k2·y’(t)-k1·y(t)=-mg+Fвын
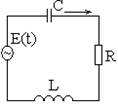
Задача №2 Происходит колебание тока, ток идет в двух направлениях
По закону Ома:
Эти уравнения фактически одинаковы, т.е. для двух разных систем уравнения, описывающие колебания фактически одинаковы. Следовательно, механическую систему можно изучить при помощи элементарных систем и наоборот. Принцип позволяющий представлять сложные системы при помощи простых – это и есть моделирование. Пусть есть система А, которая обладает набором свойств S, моделью данной системы будем называть А’. Она будет обладать аналогичным набором свойств S’ похожих на S. При изучении мы можем заменить А с S на А’ с S’ – эту систему называют моделью.
Процесс моделирования – это построение модели для механических систем и изучение свойств модели. Классификация моделей
Рабочие модели (искусственное сердце, печень, почки – это модели копирующие основные свойства органов) – это системы обладающие теми же свойствами, предназначены не для изучения, а для замены. Исследовательские модели – созданы для изучения свойств исходного объекта, которого сложно изучать. Экспериментальные модели – это реальные системы, которые обладают свойствами исходной системы. Подобие (по внешним признакам) для изучения свойств зависящих от внешних признаков (моделируется только форма, например, самолет). Аналогия – системы внешне разные, но обладают аналогичными свойствами. Гибридные – такие модели сочетают и аналогию и подобие (например, обучение пилота перед монитором, т.е. подобие – кабина, аналогия – реакция модели на действие пилота). Теоретические модели – модель существует теоретически на бумаге или в компьютерном виде. Общего вида – глобальные теории (всемирного тяготения и т.д.) охватывают общие свойства окружающего мира. Специальные теории – теории в отдельных областях знаний. Детерминированные – эти модели описываются при помощи дифференциальных уравнений. Стохастические – это модели, в которых применяются методы теории вероятности поведения таких систем на постоянное воздействие и присутствуют различные результаты. Агрегативные модели – это модели, которые допускают декомпозицию на более простые модели. Примеры основных случайных величин и их характеристик 1) Случайная величина X, закон Бернулли
X – число появлений события А из n независимых опытов.
2) Закон распределения Пуассона
λ – среднее число соединений в единицу времени. 3)
4) Равномерный закон распределения
5) Нормальный закон распределения (f (x, m, σ))
X=x1+x2+x3+…+xn, Если n достаточно велико, то X имеет нормальный закон распределения. При моделировании достаточно n=12. 6) Закон треугольника.
Площадь под кривой для плотности распределения равна единице.
Применяют в тех случаях, если кривая похожа на треугольник. Корреляционный момент Двумерная случайная величина X(ξ, η), Начальным моментом порядка k,l – называется мат ожидание от произведения.
Центральные моменты – это мат ожидание центрированных величин.
Корреляционный момент.
Дисперсия корреляционного момента:
Теорема: Если две случайные величины независимы между собой, то их корреляционный момент равен 0. Доказательство: Дано: Две независимые случайные величины.
Теорема доказана. Обратное утверждение неуместно! Если корреляционный момент двух случайных величин отличен от нуля, то они называются коррелированными. Корреляционный момент служит для определения являются ли две случайные величины зависимы между собой. На практике если определили, что k≠0 то случайные величины зависимы, а если k=0, то либо независимы, либо коррелированны. Коэффициент корреляции:
Конспект лекций по моделированию систем
Выполнил студент: группы ИТ-424 Вафина И. А. Преподаватель: Замыслов В.Е.
2007 г. Содержание: § 1. Основные понятия. 3 § 2. Классификация моделей. 5 § 3. Этапы составления и исследования моделей. 6 § 4. Имитационное моделирование. 8 § 5.Элементы теории вероятности. 10 Способы вычисления вероятности. 10 § 6.Примеры основных случайных величин и их характеристик. 14 § 7.Построение датчика псевдослучайных чисел. 16 § 7.1 Датчики для равномерного закона распределения. 16 § 7.2 Построение датчика псевдослучайных чисел для любого закона распределения 16 § 7.3 Построение датчика по показательному закону распределения. 17 § 7.4 Построение датчика с помощью таблицы квантилей. 18 § 8. Потоки случайных событий. Пуассоновский поток. 19 § 9.Связь потока Пуассона с показательным законом распределения. 21 § 11. Моделирование работы конечного автомата. 24 §12. Моделирование работы системы массового обслуживания. 27 § 13. Двумерные случайные величины и их законы распределения. 34 § 14.Понятие зависимых и независимых случайных величин. 36 §15 Условное математическое ожидание линии регрессии. 38 §16 Числовые характеристики двумерных случайных величин. 39 Корреляционный момент. 39 §17 Виды зависимости между случайными величинами. 42 §18 Нахождение на практике линейной регрессии. 45
Понятия модели и моделирования. Для определения этих понятий необходимо рассмотреть следующие задачи: Задача №1 По рельсу катиться колесо, нужно определить какие силы действуют на колесо
Fупр=-k1·y(t) жесткость пружины- закон Гука Fс=-k2·y’(t) 2 закон Ньютона my’(t)= k1·y(t)-k2·y’(t)-mg+Fвын my’’(t)+k2·y’(t)-k1·y(t)=-mg+Fвын
Задача №2 Происходит колебание тока, ток идет в двух направлениях
По закону Ома:
Эти уравнения фактически одинаковы, т.е. для двух разных систем уравнения, описывающие колебания фактически одинаковы. Следовательно, механическую систему можно изучить при помощи элементарных систем и наоборот. Принцип позволяющий представлять сложные системы при помощи простых – это и есть моделирование.
Пусть есть система А, которая обладает набором свойств S, моделью данной системы будем называть А’. Она будет обладать аналогичным набором свойств S’ похожих на S. При изучении мы можем заменить А с S на А’ с S’ – эту систему называют моделью. Процесс моделирования – это построение модели для механических систем и изучение свойств модели. Классификация моделей
Рабочие модели (искусственное сердце, печень, почки – это модели копирующие основные свойства органов) – это системы обладающие теми же свойствами, предназначены не для изучения, а для замены. Исследовательские модели – созданы для изучения свойств исходного объекта, которого сложно изучать. Экспериментальные модели – это реальные системы, которые обладают свойствами исходной системы. Подобие (по внешним признакам) для изучения свойств зависящих от внешних признаков (моделируется только форма, например, самолет). Аналогия – системы внешне разные, но обладают аналогичными свойствами. Гибридные – такие модели сочетают и аналогию и подобие (например, обучение пилота перед монитором, т.е. подобие – кабина, аналогия – реакция модели на действие пилота). Теоретические модели – модель существует теоретически на бумаге или в компьютерном виде. Общего вида – глобальные теории (всемирного тяготения и т.д.) охватывают общие свойства окружающего мира. Специальные теории – теории в отдельных областях знаний. Детерминированные – эти модели описываются при помощи дифференциальных уравнений. Стохастические – это модели, в которых применяются методы теории вероятности поведения таких систем на постоянное воздействие и присутствуют различные результаты. Агрегативные модели – это модели, которые допускают декомпозицию на более простые модели.
|
|||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 369; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.129.119 (0.009 с.) |








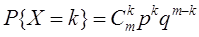


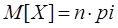
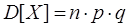
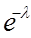





 Показательный закон распределения непрерывной случайной величины.
Показательный закон распределения непрерывной случайной величины.
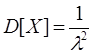

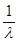 - среднее время ожидания, f(x) – функция плотности.
- среднее время ожидания, f(x) – функция плотности.
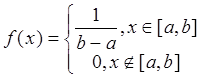



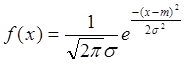
 ,
, 



 ,
, 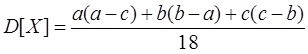
 ,
, 

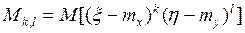
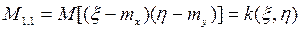
 - основная формула корреляционного момента.
- основная формула корреляционного момента.

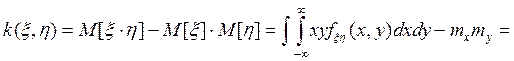

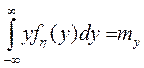


 - среднеквадратические отклонения.
- среднеквадратические отклонения.



