
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Двумерные случайные величины и их законы распределенияСодержание книги
Поиск на нашем сайте
Пусть есть опыт, в котором несколько случайных величин
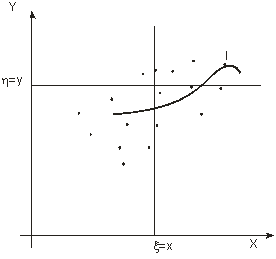
X(S, h, Δτ, r) – многомерные случайные величины Будем рассматривать только двумерные случайные величины X(ξ, η), где ξ и η - случайные величины со своими законами распределения. Геометрическая интерпретация:
y– значение η
Двумерные случайные величины подразделяются на непрерывные и дискретные случайные величины. Дискретная случайная величина – это такая случайная величина (точка), вокруг которой, сколько бы раз ни проводили опыт, не никаких других точек, т.е. все точки изолированы друг от друга. Непрерывная случайная величина – это такая случайная величина, значения которой заполняют сплошь некоторую область на плоскости.
Закон распределения дискретной случайной величины (если задана таблица):
Закон распределения непрерывной случайной величины задается в виде функции распределения – вероятность происхождения двух событий одновременно.
Механический смысл ≈ масса плоскости (D)
Функция плотности распределения:
Понятие зависимых и независимых случайных величин Пусть в опыте есть двумерная случайная величина X(ξ, η)
Рассмотрим
Измеряем вес и рост определенного человека, затем фиксируем рост => люди будут иметь разный вес
Условный закон распределения – это закон распределения, когда какая-нибудь компонента известна.
Случайная величина ξ независима от η, если для любого значения
Это понятие взаимное, т.е. если ξ не зависитот η, то и η не зависитот ξ. Если условие не выполняется Теорема: Две случайные величины ξ и η в одном и том же опыте будут являтся независимыми случайными величинами тогда и только тогда, когда их двумерный закон распределения равен произведению одномерного закона.
Если нарушаются эти условия, то ξ и η – зависимы. Доказательство: Дано ξ и η –независимые случайные величины =>
Если не зависимы
Теорема доказана. Условное математическое ожидание линии регрессии.
Условное мат. ожидание
Мат. Ожидание, посчитанное при условии, что одна координата зафиксирована
l – линия регрессии, состоящая из условных мат. ожиданий (регрессия y по х). l: Вид зависимости между двумя случайными величинами определяется формой линии регрессии. Пример:
Числовые характеристики двумерных случайных величин Корреляционный момент Двумерная случайная величина X(ξ, η), Начальным моментом порядка k,l – называется мат ожидание от произведения.
Центральные моменты – это мат ожидание центрированных величин.
Корреляционный момент.
Дисперсия корреляционного момента:
Теорема: Если две случайные величины независимы между собой, то их корреляционный момент равен 0. Доказательство: Дано: Две независимые случайные величины.
Теорема доказана. Обратное утверждение неуместно! Если корреляционный момент двух случайных величин отличен от нуля, то они называются коррелированными. Корреляционный момент служит для определения являются ли две случайные величины зависимы между собой. На практике если определили, что k≠0 то случайные величины зависимы, а если k=0, то либо независимы, либо коррелированны. Коэффициент корреляции:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 244; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.140.253.240 (0.01 с.) |


 x – значение ξ
x – значение ξ




 x,y – не включаются в интервал
x,y – не включаются в интервал

 - плотность, с которой единичная масса распре делена на плоскости.
- плотность, с которой единичная масса распре делена на плоскости.
 - закон распределения для случайной величины ξ
- закон распределения для случайной величины ξ - закон распределения для случайной величины η
- закон распределения для случайной величины η


 - рост
- рост - вес
- вес - закон распределения веса. Он будет один и тот же для разного роста.
- закон распределения веса. Он будет один и тот же для разного роста.

 , то случайные величины зависимы.
, то случайные величины зависимы.

 Рассмотрим прямоугольник с бесконечно малыми сторонами. Р – вероятность попадания в эту область.
Рассмотрим прямоугольник с бесконечно малыми сторонами. Р – вероятность попадания в эту область.



 Рассмотрим векторную величину Х(ξ,η).
Рассмотрим векторную величину Х(ξ,η).
 зафиксирована η.
зафиксирована η. - условное мат ожидание.
- условное мат ожидание. Линия регрессии – ориентировочный средний вес в данном примере.
Линия регрессии – ориентировочный средний вес в данном примере. ,
, 

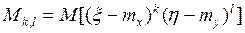
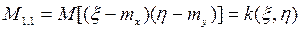
 - основная формула корреляционного момента.
- основная формула корреляционного момента.

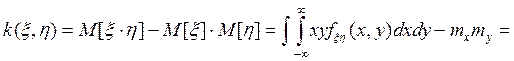

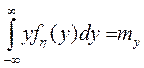


 - среднеквадратические отклонения.
- среднеквадратические отклонения.



