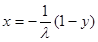Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Способы вычисления вероятностиСодержание книги Поиск на нашем сайте
1) Схема случаев. Опыт сводится к схеме случаев, если обладает свойствами: - число элементарных исходов конечно; - элементарные исходы попарно несовместны; - все исходы равновозможные.
P(А)=m/n, где n – число элементарных исходов m – число исходов благоприятного появления А
2) Статистическое определение вероятности. Опыт: случайное событие А, N – число проведенных опытов, n – появлений событий А. PN*(А) = n/m - частота появления события А.
Замечание: Частота стремится в основном к вероятности. Будут отклонения, но с ростом число таких отклонений в процентном состоянии стремится к 0
Случайная величина – это любая числовая функция на множестве Ω, областью определения которой является множество Ω, а область значений множество действительных чисел. Пространство элементарных исходов есть некоторое множество, в которое входят все элементарные исходы.
Для описания случайных величин используют законы распределения случайных величин. Представление дискретной случайной величины:
Пример: для кубика выглядит так
Представление непрерывной случайной величины: Функция распределения Механический смысл закона распределения длядискретной случайной величины:
Для непрерывной случайной величины:
x1<x2, F(x1)≤ F(x2)
F(x) – монотонно возрастающая функция
Механическая аналогия – это плотность массы, с которой вероятность размазана по всей числовой оси
Числовые характеристики 1) X – случайная дискретная величина
Математическое ожидание – это средняя точка, около которой разбросаны значения вероятностей
X – непрерывная случайная величина
Здесь M[X] – центр тяжести системы материальных точек.
2) Дисперсия – характеризует величину разброса случайных значений вокруг математического ожидания.
3) Среднеквадратическое отклонение от математического ожидания
Примеры основных случайных величин и их характеристик 1) Случайная величина X, закон Бернулли
X – число появлений события А из n независимых опытов.
2) Закон распределения Пуассона
λ – среднее число соединений в единицу времени. 3)
4) Равномерный закон распределения
5) Нормальный закон распределения (f (x, m, σ))
X=x1+x2+x3+…+xn, Если n достаточно велико, то X имеет нормальный закон распределения. При моделировании достаточно n=12. 6) Закон треугольника.
Площадь под кривой для плотности распределения равна единице.
Применяют в тех случаях, если кривая похожа на треугольник. Построение датчика псевдослучайных чисел. Те числа, которые получаются с помощью датчика – псевдослучайные числа. Массивы чисел, которые получаются с помощью генераторов - псевдослучайны, т.к. они получены с помощью определенных алгоритмов. x=rand(m,n), 0≤xij≤1 распределена по равномерному закону.
Датчики для равномерного закона распределения
x1=0,5 {} – другая часть числа x2={11x1+π} {π} = 0,1415926… x3={11x2+π} Если увеличивать закон выборки
Чтобы построить гистограмму нужно использовать команду hist(x,100), где x – выборка, 100 – количество интервалов, на которых находится выборка.
Построение датчика псевдослучайных чисел для любого закона распределения Теорема: Пусть ξ – случайная величина распределенная по закону y=Fξ(x).
Утверждается, что случайная величина η распределена по равномерному закону. Доказательство: ξ – равномерный закон распределения
Возьмем произвольный интервал и найдем вероятность попадания в этот интервал, причем вероятность зависит от длины интервала. Это и будет означать, что случайная величина η распределена по равномерному закону.
Следствие: Если
Построение датчика по показательному закону распределения ξ – показательный закон распределения, если
При x ≥ 0,
1. Генерируем 2.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 248; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.146.107.223 (0.009 с.) |

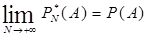


 Ω={w}
Ω={w}

 mi=1/6, где i – это каждая точка.
mi=1/6, где i – это каждая точка.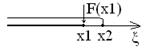
 ,
, 

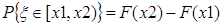


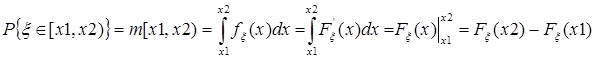






 Механический смысл – координаты точки, момент инерции.
Механический смысл – координаты точки, момент инерции.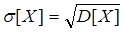

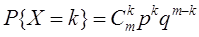


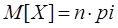
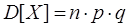
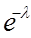





 Показательный закон распределения непрерывной случайной величины.
Показательный закон распределения непрерывной случайной величины.
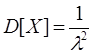

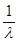 - среднее время ожидания, f(x) – функция плотности.
- среднее время ожидания, f(x) – функция плотности.
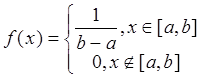



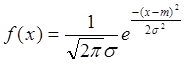
 ,
, 



 ,
, 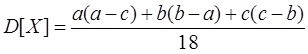



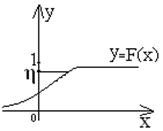
 , η - случайная величина, распределенная от 0 до 1.
, η - случайная величина, распределенная от 0 до 1.



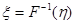 .
.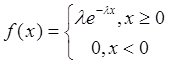

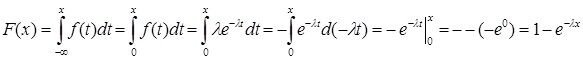
 .
.


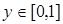 по равномерному закону распределения
по равномерному закону распределения