Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Построение датчика с помощью таблицы квантилейСодержание книги
Поиск на нашем сайте
Очень часто при построении датчиков обратную функцию для функции распределения найти невозможно или очень трудно. Тогда используют квантили.
Квантиль значения Р – это значение функции в точке
Построение таблицы квантилей: Отрезок [0,1] разбивается на равных N частей
Алгоритм построения квантилей: 1) Генерируется случайное число 2) Определяется номер интервала. Положим
3) Находим пару квантилей, которые являются границами найденного интервала
4) Генерируем случайную величину t по равномерному закону
Потоки случайных событий. Пуассоновский поток.
Поток событий – это последовательность псевдослучайных однотипных событий в случайные моменты времени. Поток называется простейшим или Пуассоновским, если он обладает следующими свойствами: 1) одинарность – события потока следуют по одиночке; 2) стационарность – вероятность того, что за промежуток Δt произойдет ровно m событий потока, одно и тоже независимо от того, где Δt берется; 3)
Теорема:
где λ – среднее число событий потока за единицу времени M – математическое ожидание,
Доказательство: Формула Бернулли А – случайное событие, Р(А),
Докажем, что простейший поток всегда будет Пуассоновским. Рассмотрим ΔT
Рассмотрим случайную величину ξ – число событий потока на интервале
В силу одинарности таблица ограничена двумя значениями. Определим q, p
Эксперимент в силу стационарности повторяется n – раз.
=[Пусть: n→∞. В пределе формула Бернулли перейдет в формулу Пуассона. λΔT=a.]=
=[Поделим на n]=
Теорема доказана. Связь потока Пуассона с показательным законом распределения Пусть существует Пуассоновский поток
Теорема: Промежуток времени между двумя соседними событиями Пуассоновского потока есть случайная величина, имеющая показательный закон распределения с тем же показателем λ – что и Пуассоновского потока и наоборот. Дано: поток простейший. Доказательство: Δt - промежуток времени между двумя соседними событиями имеет показательный закон распределения с тем же параметром λ.
Теорема доказана. Минимизация конечных автоматов.
Алгоритм эквивалентных пар Алгоритм начинается с построения таблицы эквивалентных пар Автоматная таблица:
По автоматной таблице составляем таблицу пар: Таблица 1.
(2,9), (4,9), (6,9) дальше не будут давать эквивалентные значения на выходе. Таблица 2.
Алгоритм минимизации:
1) Составление таблицы пар, для которых выходные сигналы одинаковы, и заполнение этой таблицы парами, которые переходят в пары первого столбца при первом входном сигнале. 2) Отмечаются строчки таблицы, в которых есть различимые пары, отсутствующие в первом столбце. Различимая пара – это пара, в которой два разных состояния. Отметить строчку – это, значит, отметить пару первого столбца этой строки. (Этот шаг повторяется в цикле)
3) Отмечают строчки, в которых есть пары отмеченные в первом столбце. Эквивалентными будут те пары, которые остались не отмеченные. Составим автоматную таблицу для состояний 1-5. Таблица. 3
1) Берем ст. 1 из строящейся табл. 3 2) Смотрим из табл.2 какие цифры соответствуют. 3) Из табл.1 выбираем по полученным цифрам строки и по табл.2 в табл.3 записываем полученные состояния.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 202; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.84.179 (0.008 с.) |

 P – это обозначение некоторой вероятности, она выражается числом на промежутке (0,1)
P – это обозначение некоторой вероятности, она выражается числом на промежутке (0,1) .
. всего (N+1) точек
всего (N+1) точек Из-за практических соображений а и b выбирают такие, что все случайные значения заключены между ними.
Из-за практических соображений а и b выбирают такие, что все случайные значения заключены между ними.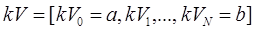
 по равномерному закону
по равномерному закону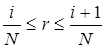 , находим i – номер интервала
, находим i – номер интервала



 , где r1 – равномерно распределенная случайная величина на промежутке [0,1].
, где r1 – равномерно распределенная случайная величина на промежутке [0,1].
 отсутствие последействия – число событий на промежутке ΔT2 не зависит от того сколько событий произошло на промежутке ΔT1 (нынешняя ситуация не влияет на последующую)
отсутствие последействия – число событий на промежутке ΔT2 не зависит от того сколько событий произошло на промежутке ΔT1 (нынешняя ситуация не влияет на последующую)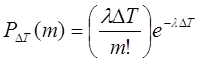 ,
, ,
, - вероятность того, что за ΔT произойдет m событий.
- вероятность того, что за ΔT произойдет m событий.


 - среднее число событий за
- среднее число событий за 
 ;
; 
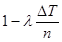



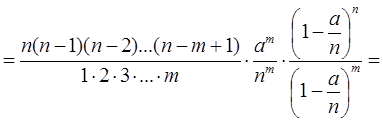
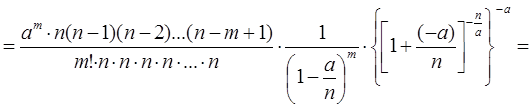


 Δt – непрерывная случайная величина
Δt – непрерывная случайная величина
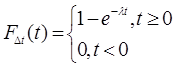

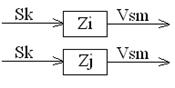
 - два состояния конечного автомата эквивалентны, если при воздействии на автомат любой последовательности входных сигналов получаем одинаковую последовательность выходных сигналов.
- два состояния конечного автомата эквивалентны, если при воздействии на автомат любой последовательности входных сигналов получаем одинаковую последовательность выходных сигналов.