
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ступенчатая матрица. Теорема о приведении матрицы к ступенчатой матрице.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Ступенчатая матрица. Теорема о приведении матрицы к ступенчатой матрице. Опр. Матрица А наз. ступенчатой если выполнены условия: Если i -тая строка нулевая, i +1 – нулевая. Если лидеры строк i и i+ 1 находятся в столбцах k и l, то k < l. Всякая нулевая матрица явл. ступенчатой. Если в ступенчатой матрице удалить или дописать нулевые строки то она остается ступенчатой. Теорема. Пусть в матрице А, а ik ≠ 0, тогда если к j-той строке прибавить i-тую умн. (- Теорема. Всякую матрицу можно привести к ступенчатой матрице за конечное число элементарных преобразований. Д- во: Если А=0, то А – ступенчатая. Пусть А ≠ 0, тогда матрица содержит хотя-бы одну строку с ненулевым эл-том. (лидер ≠ 0) Если таких стр. несколько, то выберем ту стр. у которой лидер имеет меньший порядковый номер. Зафиксируем строку поменяем с первой. Поступаем аналогично для строк начиная со 2-ой стр. и т.д.
3°. Системы линейных уравнений (СЛУ). Решение СЛУ. Эквивалентные СЛУ. Однородные СЛУ. СЛУ с m-уравнениями и n-переменными наз. совокупность m-уравнений с n-неизвестными.
(1)
Здесь x1, x2, …, x n — неизвестные, которые надо определить. a 11, a 12, …, a mn — коэффициенты системы; b1, b2, … b m — свободные члены — предполагаются известными. Индексы коэффициентов (a ij) системы обозначают номера уравнения (i) и неизвестного (j), при котором стоит этот коэффициент, соответственно. Система (1) называется однородной, если все её свободные члены равны нулю (b1 = b2 = … = bm = 0), иначе — неоднородной. Решением СЛУ (1) наз. Строка (α1, …, α2) которая является решением каждого из n-ур-ний. Решить СЛУ – значит найти все решения или доказать что их нет. Две СЛУ наз. эквивалентными если множество их решений совпадает.
Миноры и их алгебраические дополнения. Теорема Лапласа. Определителем (или детерминантом) n -го порядка называется число D, равное алгебраической сумме n членов, составленных определенным образом из элементов
Алгебраическим дополнением Минором
Теорема Лаплпса: Если в определителе зафиксировать k-строк, то определитель равен сумме всевозможных произведений миноров k-го порядка, стоящих в k-тых строках на их алгебраич. Дополнения.
8°. Обратная матрица. Обра́тная ма́трица — такая матрица A−1, при умножении на которую исходная матрица A даёт в результате единичную матрицу E:
Для матрицы А существует обратная тогда и только тогда, когда она невырожденная, то есть её определитель не равен нулю. Для неквадратных матриц и вырожденных матриц обратных матриц не существует. Обратная матрица вычисляется по формуле:
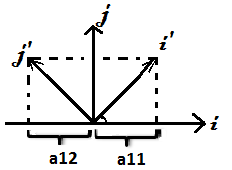
Теорема о разложении вектора на плоскости по двум неколлинеарным векторам. Теорема. Пусть дана некоторая плоскость π и векторы
Доказательство: АА1||OE2, AA2||OE1, зн. OA2AA1-параллелограмм OA1||OE1, Докажем, что такое разложение единственное: Предположим, что это разложение не единственное.
т.к. x-x1=0, x=x1; y-y1=0, y=y1; 14. Теорема о разложении вектора в пространстве по трем некомпланарным векторам. Теорема. Пусть
Док-во св-ва 4:
↑ однородная СЛУ Док-во св-ва 6: (О;
A(x1, y1); B(x2, y2)
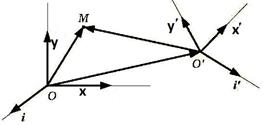
20. Преобразование прямоугольных координат.
M(x,y); ϕ
x (x- a 1-x’cosϕ+y’sinϕ)
x=x’cosϕ-y’sinϕ+ a 1 y=x’sinϕ+y=cosϕ+ a 2
Угол между прямой и плоскостью. ∆:
sin
Исследование формы эллипса Пусть х2/а2+у2/b2=1, где b2=a2-c2 F 1 (-c,0) F 2 (c,0) 1)y2=b2/a2(a2-x2) => x2≤a2, |x|≤a x=a, x=-a; X2=a2/b2(b2-y2) => y2≤b2, |y|≤b y=b, y=-b; Все точки эллипса расположены внутри прямоугольника, ограниченного прямыми. 2) M 1 (x1,y1) принадлежит эллипсу, то M 2 (-x1,y1), M 3 (-x1,-y1), M 4 (x1,-y1) принадлежат эллипсу Эллипс симметричен относительно оси О х,О у и начало координат. О(0,0) – центр эллипса. Будем исследовать эллипс только в 1-ой четверти X≥0, y≥0 y2= y= если х=0, то у=b если х возрастает, то у убывает если х=а, то у=0 А1(-а,0), А2(а,0) вершины эллипса В1(-b,0), B2(b,0) Опр. Прямая, проходящая через фокусы называется факальной осью. Опр. Расстояние от центра эллипса до вершины факальной оси называется большей полуосью (а) Опр. Расстояние от эллипса до вершины факальной оси называется меньшей полуосью.(b-меньшая полуось) Опр. Число равное отношению расстояния между фокусами к расстоянию между вершинами факальной оси наз. эксцентриситетом (степень сжатия окружности из которой получится эллипс) ε<1. Опр. Отрезок, соединяющий точку эллипса сфокусам называется факальным радиусом (МF 1,MF 2) МF 1 =a+(c/a)x=a+εx MF 2 =a-(c/a)x=a+εx Опр. Длина перпендикуляра восстановленного из фокуса до пересечения с эллипсом наз. Факальным араметром Р. Факальный параметр p=b2/a Оптическоесв-во эллипса X2/9+y2/25=1 c2=16 c=4; x’=y, y’=x. F1(-4,0)F2(4,0) X’2/25+y’2/9=1 b2=a2-c2 Исследование формы параболы Пусть у2=2рх – каноническое уравнение параболы в специально выбранной системе координат. Чем больше р, то больше расходятся ветви и наоборот. Т.к. р>0, y2≥0, то x≥0. Если точка M1(x1, y1) принадлежит параболе, то точка M2(x1, -y1) принадлежит параболе, парабола симметрично оси Ох.
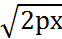
Если х=0, то у=0 О(0, 0)- вершина параболы. Если х возрастает, то у возрастатет. Опр. Факальной осью параболы называется прямая, проходящая через фокус перпендикулярно директрисе. Опр. факальный параметр= р Примеры: 1)у2=-2рх – неканоническое уравнение параболы х’=y, y’=x.F(-p/2, 0) Ветви параболы наклонены по оси Ох во II-ой и III –ей четверти. 2)х2=2ру у=-р/2 у=у’; F(0, p/2) Ветви параболы наклонены по оси Oy в I – ой и II-ой четвертях 3)х2=-ру х’=-y, y’=x; y=p/2 F(0, -p/2) Ветви параболы наклонены по оси ОуIII-ей и IV-ой четвертях.
Бинарные отношения. Бинарным отношением,заданным на множестве А, называется подмножество R≤А²(А×А). Если a и b є А, то aRb(элемент а находится в бинарном отношении R с элем.b). Пусть на множ. А задано бин.отнош.R, тогда,если R=A²,то назыв. универ сальное бинарное отношение,если R=0,то R-пустое бин.отнош.Опр.Б.о.R назыв. 1) рефлексивным,если aRa; 2) симметричным,если aRb→bRa; 3) транзитивным,если aRb, bRc→aRc; 4) антисимметричным, если aRb, bRa→a=b. 70°. Отношение эквивалентности и порядка. Отношение эквивалентности и порядка.Б.о.R наз.отношением эквивалентности,если R-рефлексивно,симметрично и транзитивно. Опр. Пусть R-отнош.экв. аєА.Множество ā={xєA|aRx}назыв. классом эквивалентности элем. а. Теорема:любых два класса эквивалентности либо не пересекаются, либо совпадают. Опред:если на множ.А задано отнош.эквив. ̴,то совокупность всевожможных непересекающихся классов эквив. наз. фактор-множеством(А ̰).Б.о. наз. отнош.частичного порядка,если рефл., антисимм., транзитивно.Элем. a и b-сравнимые,если aRb или bRa, в противном случае они несравнимы.
71°. Алгебраическая операция. Свойства алгебраических операций. Свойства алг.опер. Пусть X-непустое множество. Говорят,что на множестве Х задана алг. опер., если указано правило, по которому двум любым элементам этого множества ставится в соответствие вполне определённый элемент этого множества. Элем.nєX наз. нейтральным, если n◦a=a◦n=a. Алг.опер. наз. ассоциативной, если a◦(b◦c)=(a◦b)◦c.Пусть на Х задана алг.о. Элем. aєX наз.симметричным к bєX, если a◦b=b◦a=n.Алг. о. наз.коммутативной,если a◦b=b◦a. Свойства: 1)если существует n.,то он единственный; 2)симметричный элем- единственный.
72°.Определение группы.Простейшие свойства групп. Непустое множество G наз. группой,если на нём задана алг. опер.,удовл.условиям:G1)◦ -ассоц-на a◦(b◦c)=(a◦b)◦c;G2)сущ-ет nєG; n◦a= a◦n =a;G3)для люб. a◦G сущ. b симметр.эл. a◦b=b◦a=n.G4)Группа наз. коммутата тивной (абелевой), если ◦ -коммут. опер., т.е. a◦b=b◦a. Свойства:1)n-единств-й;2)для люб. a,bєG уравнения ax=b,ya=b – им.единственные решения; 3)обратным элем к произв.(ab)-1=b-1a-1. Группа, на которой задана опер. «сложения»-аддитивная, «умножения»-мультипликативная.
73°. Определение кольца. Простейшие свойства колец. Непустое множество К наз.кольцом,если на нём заданы 2 алг. оп. «+», «*»,для которых выполняются аксиомы:К1)К явл.абелевой группой относит. «+»(проверить G1,G2,G3,G4) К2)опер «*умн.»-ассоц-на, т.е. a*(b*c)=(a*b)*c;К3)умнож.дистрибутивно отностит.оп. сложения,т.е. a*(b+c)=a*b+a*c. Опр: кольцо назыв. коммутативным кольцом, если опер. умн.коммут-на К4)a*b=b*a. Опр: коль цо К наз.кольцом с единицей,если К5) существует nєК n*a=a*n=a. Свойства: 1) кольцо явл.коммутат.гр., значит для него вып-ся все св-ва групп 2) в кольце можно ввести опер. вычитания; 3) если a*0=0*a=0; a*b=0; a 4) если а не является делителем 0, то a*b=a*c→ b=c; 5) (-a)*b=a*(-b)=-(a*b); 6) if K-кольцо с 1,то оно единственно; 7) К(кольцо с обратн. эл.)- группа отн.умнож.
74°.Определение поля.Простейшие свойства поля. Коммутативное кольцо с единицей, в котором все элементы кроме 0 обратимы наз. полем. Вып. усл. (К1-К5). Свойства: 1) для полей верны все св-ва колец К1) К явл.абелевой группой относит. «+»(проверить G1,G2,G3,G4) К2) опер «*умн.»-ассоц-на, т.е. a*(b*c)=(a*b)*c; К3) умнож. дистрибутивно отностит. оп. сложения, т.е. a*(b+c)=a*b+a*c. Опр: кольцо назыв. коммутативным кольцом, если опер. умн.коммут-на К4)a*b=b*a.Опр: кольцо К наз. кольцом с единицей,если К5) существует nєК n*a=a*n=a.;
2) в поле нет делитителей 0; 3)ax=b-единств.реш.,если aǂ0.
Изоморфизмы групп, колец. Группы G1,G2 наз.изоморфными,если существует взаимооднозначное соответствие(биекция)f:G1→G2; f(a◦b)=f(a)*f(b) f-изоморфизм. Опр. Кольцо К1 и К2 наз. изоморфными, если сущ. биекция f:K1→K2; f(a+b)=f(a)+f(b);f(a*b)=f(a)*f(b) C1 Свойства изом.группы: 1)G 2)G 3)G Множество групп разбивается на взаимно непересекающиеся классы изоморфных групп.
76⁰.Построение поля комплексных чисел.Алгебраическая форма комплексного числа. Пусть z1=a1+b1i, z2=a2+b2i принадлежат С, z1=z2,если a1=a2,b1=b2. Опр. Суммой двух элементов z1 и z2єС наз.эл. Опр. Произведением Теорема. Множество С={a+bi|a,bєR} с операциями сложения и умн. явл-ся полем. Зам:каждый ненулевой элемент множества обратим. Опр. Пусть z=a+bi є C Опр. Пусть z=a+bi є C; a=Rez-действит. часть компл.числа;b=Imz-мнимая часть; a+0i – действительные числа; 0+bi – мнимые числа.
77°.Тригонометрическая и экспоненциальная форма записи комплексного числа.Действия над компл. числами в триг.и экспон.форме записи. Рассм.С={a+bi|a,bєR} z=a+bi.Каждому числу z=a+bi можно поставить в соответствие точку с координатами (a,b)в прямоугольной CK.и наоборот –это взаимно однозначное соответствие.
78°.Возведение в степень и извлечение корня n-ой степени из комплексного числа. Опр. z0=1;z1=z;zn=z*z*z… Опр. Z-n=
Св-ва.
Опр. Многочлен кот.явл.делителем 2 других многочленов наз. Их общих делителем. Опр. Наибольшим общим делителем f(x) и g(x) наз. Их общий делитель кот. Делится на все остальные их общие делители. Нод определен с точностью до числового множества. Нод(f(x),g(x))=d(x) Опр. Многочлены наз. Взаимно простыми., если НОД их явл. Многоченом нулевой степени Теорема. Если f(x)=g(x)*q(x)+r(x), то НОД многочлен f(x),g(x), такой же НОД(g(x),f(x)). АЛГОРИТМ ЕВКЛИДА Найти НОД (f(x),g(x)). Пусть Deg f(x) ≥ deg g(x), если f(x) g(x)=r1(x)*q2(x)+r2(x), если r2!=0, то r1(x)=r2(x)*q3(x)+r3(x)… rn-1=rn(x)*qn+1(x) теорема. Если d(x)=НОД(f(x),g(x))
Критерий взаимнопростые многочлены:f(x) и g(x)-взаимопростые
Св-ва неприводимого мн-чл. 1)Если f(x) – неприводим, а α – элемент поля, α!=0, то α(f(x)) - неприводим 2)Многочлен 1-ой степени над любым полем неприводим 3)Если f(x) – неприводим, g(x) – произвольный мн/чл., то либо g(x) ТЕОРЕМА Всякий многочлен можно представить в виде произведения неприводимого многочлена, причем данное разложение единственно с точностью до числового множителя и порядка следования множителей.
84°. Корни многочлена от одной переменной. Схема Горнера. Пусть ОПР. Элемент С взятый из поля F, называется корнем многочлена f(x)
Теорма Безу: Элемент С явл. Корнем f(x), тогда и тока тогда, когда
СХЕМА ГОРНЕРА q(x)=b0xn-1 + b1xn-2 +…+ bn-2x + bn-1
Опр. Пусть с-корень f(x). C-наз.K- Кратным корнем f(x), если Теорема. Многочлен в степени n имеет n-корень, при этом если многочлен разложен на первую степень, то он имеет n-четное кол-во корней.
ТЕОРЕМА Всякую правильную дробь можно представить в виде суммы простейших Д-во: . 1= F(x) = . Теорема. Всякую простейшую дробь знаменатель кот. Стоит степень не приводимого многочлена. 87°. Многочлены с рациональными коэфициентами. Нахождение корней многочленов с рациональными коэфициентами. пусть f(x) ai пусть f(x) всякий корень f(x) явл корнем g(x) и наоборот. ТЕОРЕМА Пусть f(x) Пример Нахождения корней многочленов с рациональными коэфициентами f(x) = 2x3 + 3x2 + 3x + 1
p = 1, -1 q = 1, -1, 2, -2 . X= 1 – не корень Х= - ½ - корень 2x3 + 3x2 + 3x + 1 = (x+1/2)*(2x2 + 2x +2) Замечание. Если число не целое то это НЕ корень!.
Ступенчатая матрица. Теорема о приведении матрицы к ступенчатой матрице. Опр. Матрица А наз. ступенчатой если выполнены условия: Если i -тая строка нулевая, i +1 – нулевая. Если лидеры строк i и i+ 1 находятся в столбцах k и l, то k < l. Всякая нулевая матрица явл. ступенчатой. Если в ступенчатой матрице удалить или дописать нулевые строки то она остается ступенчатой. Теорема. Пусть в матрице А, а ik ≠ 0, тогда если к j-той строке прибавить i-тую умн. (- Теорема. Всякую матрицу можно привести к ступенчатой матрице за конечное число элементарных преобразований. Д- во: Если А=0, то А – ступенчатая. Пусть А ≠ 0, тогда матрица содержит хотя-бы одну строку с ненулевым эл-том. (лидер ≠ 0) Если таких стр. несколько, то выберем ту стр. у которой лидер имеет меньший порядковый номер. Зафиксируем строку поменяем с первой. Поступаем аналогично для строк начиная со 2-ой стр. и т.д.
3°. Системы линейных уравнений (СЛУ). Решение СЛУ. Эквивалентные СЛУ. Однородные СЛУ. СЛУ с m-уравнениями и n-переменными наз. совокупность m-уравнений с n-неизвестными.
(1)
Здесь x1, x2, …, x n — неизвестные, которые надо определить. a 11, a 12, …, a mn — коэффициенты системы; b1, b2, … b m — свободные члены — предполагаются известными. Индексы коэффициентов (a ij) системы обозначают номера уравнения (i) и неизвестного (j), при котором стоит этот коэффициент, соответственно. Система (1) называется однородной, если все её свободные члены равны нулю (b1 = b2 = … = bm = 0), иначе — неоднородной. Решением СЛУ (1) наз. Строка (α1, …, α2) которая является решением каждого из n-ур-ний. Решить СЛУ – значит найти все решения или доказать что их нет. Две СЛУ наз. эквивалентными если множество их решений совпадает.
|
||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1795; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.78.246 (0.013 с.) |

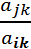 ), то в полученной матрице В эл-т b jk = 0.
), то в полученной матрице В эл-т b jk = 0.
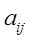 определителя. Рассмотрим определитель n -го порядка:
определителя. Рассмотрим определитель n -го порядка: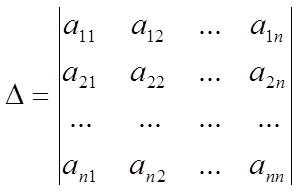 .
.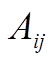 элемента
элемента 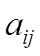 определителя n -го порядка называется определитель (n-1) -го порядка, полученный из исходного вычеркиванием i -й строки и j -го столбца и умноженный на
определителя n -го порядка называется определитель (n-1) -го порядка, полученный из исходного вычеркиванием i -й строки и j -го столбца и умноженный на 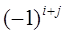 .
.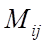 элемента
элемента 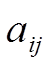 определителя n -го порядка называется определитель (n-1) -го порядка, полученный из исходного вычеркиванием i -й строки и j -го столбца, на пересечении которых находится данный элемент.
определителя n -го порядка называется определитель (n-1) -го порядка, полученный из исходного вычеркиванием i -й строки и j -го столбца, на пересечении которых находится данный элемент.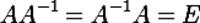
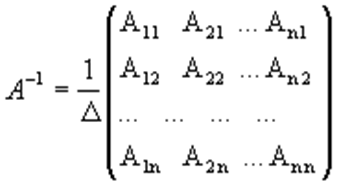 ,
, ,
,  (линейно независимость векторов), тогда любой вектор а в плоскости π можно представить в виде линейной комбинации a=x*e1+y*e2 причём данное представление единственное.
(линейно независимость векторов), тогда любой вектор а в плоскости π можно представить в виде линейной комбинации a=x*e1+y*e2 причём данное представление единственное.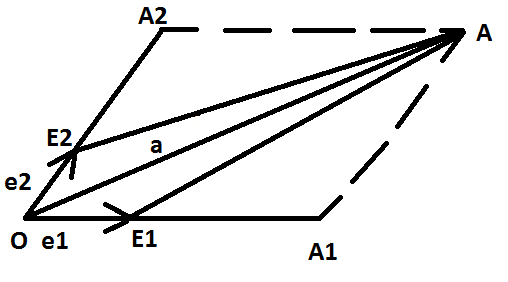
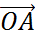 =
= 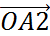 +
+ 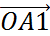 .
.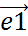 , OA2||OE2,
, OA2||OE2, 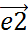 ,
,  =x*
=x* 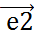 .
.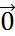
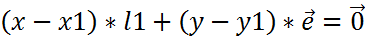
 - линейно независимые векторы, тогда любой вектор
- линейно независимые векторы, тогда любой вектор  , данное представление единственное.
, данное представление единственное.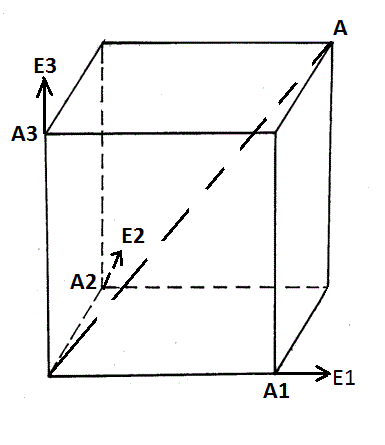
 ,
,  ,
, 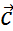 – компланарны тогда, когда
– компланарны тогда, когда 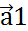 ,
, 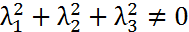 → (λ1a1+λ2b1+λ3c1; λ1a2+λ2b2+λ3c2; λ1a3+λ2b3+λ3c3)= 0,0,0
→ (λ1a1+λ2b1+λ3c1; λ1a2+λ2b2+λ3c2; λ1a3+λ2b3+λ3c3)= 0,0,0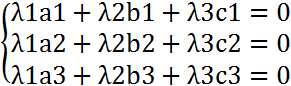 ↔ то
↔ то 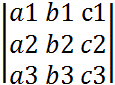 =0 ↔
=0 ↔ 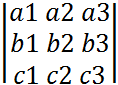 =0
=0 1;
1; 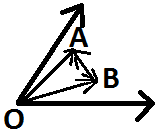
 =x1
=x1  =x2
=x2  =
=  (O,
(O, 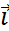 ,
, 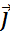 ) – «старая» (O,
) – «старая» (O, 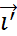 ,
, 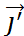 ) «новая»
) «новая» =x
=x  +y’
+y’ 
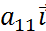 +
+ 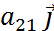 ;
; 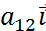 +
+ 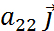
 =<(
=<(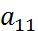 =cosϕ;
=cosϕ; 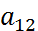 =-sinϕ;
=-sinϕ; 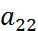 =cosϕ;
=cosϕ; 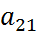 =sin ϕ
=sin ϕ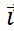 +(y- a 2-x’sinϕ-y’cosϕ)
+(y- a 2-x’sinϕ-y’cosϕ) 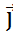 =
= 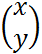 =
= 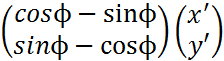 +
+ 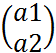
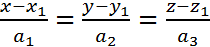 = α; π: Ax+By+Cz+D=0;
= α; π: Ax+By+Cz+D=0; =90-
=90-  (
( );
);  | =
| =  ;
;  =
= 
 (a2-x2)
(a2-x2) , Х изменяется от О до a
, Х изменяется от О до a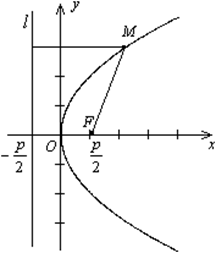
 0, b
0, b 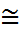 C2 – изоморфно
C2 – изоморфно .
.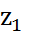 и
и 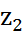 н.
н.  .
.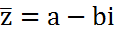 наз.комплексно-сопряж.
наз.комплексно-сопряж.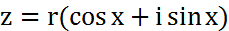 - тригонометрическая форма записи компл.числа.
- тригонометрическая форма записи компл.числа. 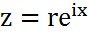 – экспоненциальная форма.
– экспоненциальная форма. 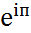 =-1.
=-1. 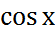 =
=  .
.  .
.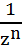 . Формула Муавра:
. Формула Муавра: 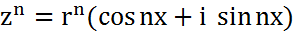 ; Опр. Корнем n-ой степени из числа z наз.число w такое, что wn=z;Если z=0,то
; Опр. Корнем n-ой степени из числа z наз.число w такое, что wn=z;Если z=0,то 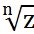 =0;если z
=0;если z 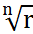 ; w=
; w=  +i
+i 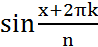 ) – корень n-ой степени.
) – корень n-ой степени.  (
(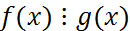 , если r(x)=0
, если r(x)=0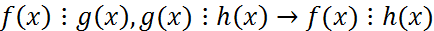
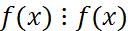
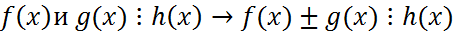
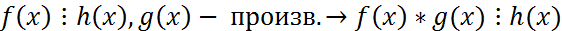
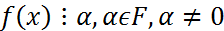
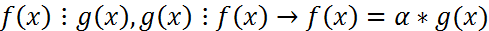
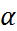 .
. g(x), тогда НОД (f(x),g(x)) = g(x), если не так, то f(x)=g(x)*q(x)+r(x): многочлен.
g(x), тогда НОД (f(x),g(x)) = g(x), если не так, то f(x)=g(x)*q(x)+r(x): многочлен.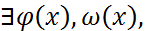
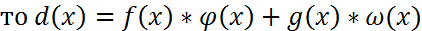
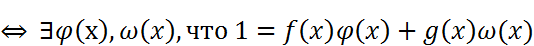
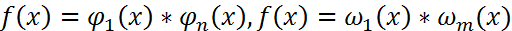
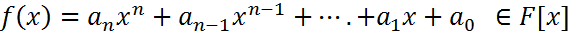 F-поле, С-элемент поля, тогда F(C)=
F-поле, С-элемент поля, тогда F(C)= 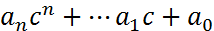 -значение многочлена при x=c.
-значение многочлена при x=c.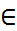 F[x], если f(C) = 0
F[x], если f(C) = 0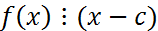
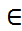 F(элемент поля), f(x)=(x-c)*q(x)+r.
F(элемент поля), f(x)=(x-c)*q(x)+r.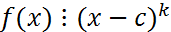 , но не делится на
, но не делится на 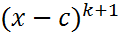 .
.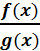 – прав-я дробь.
– прав-я дробь. 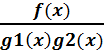 НОД (g1(x),g2(x))=1
НОД (g1(x),g2(x))=1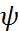 (x)g2(x) |* f(x)
(x)g2(x) |* f(x)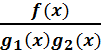 =
= 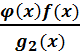 +
+ 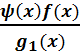
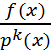 можно представить в виде суммы, k- простейших дробей в знаменателе, кот. Стоят p(x), p 2 (x)….p k (x).
можно представить в виде суммы, k- простейших дробей в знаменателе, кот. Стоят p(x), p 2 (x)….p k (x). 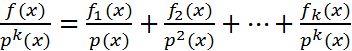 , deg f k (x)<deg p(x)
, deg f k (x)<deg p(x) Q, i=0;n
Q, i=0;n – рациональный корень многочлена, то а0
– рациональный корень многочлена, то а0  p, an
p, an  q
q : 1, -1, ½,- ½
: 1, -1, ½,- ½


