
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Правило Крамера решения систем линейных уравнений.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Система трех линейных уравнений с тремя неизвестными
Если Δ ≠ 0, то единственное решение системы (4) выражается формулами Крамера:
где Систему (4) можно записать в матричной форме:
Тогда ее решение имеет вид
если определитель матрицы А отличен от нуля. 10°. Направленный отрезок. Эквивалентные направленные отрезки. Понятие вектора. Угол между векторами. Коллинеарные и компланарные векторы.
Направленные отрезки Длиной направленного отрезка называется длина отрезка АВ. Два направленных отрезка и считаются эквивалентными, если они сонаправлены и имеют равные длины. Множество всех направленных отрезков, эквивалентных какому-нибудь одному, называется вектором. Углом между ненулевыми векторами и называется угол ВАС. Углом между любыми двумя ненулевыми векторами и называется угол между изображающими их направленными отрезками с общим началом. Угол между одинаково направленными векторами считается равным нулю, противоположно направленными —.Угол между нулевым вектором и каким-либо другим не определён. Векторы называются коллинеарными, если они расположены на одной или параллельных прямых. Нулевой вектор коллинеарен любому вектору.
Векторы называются компланарными, если существует плоскость, которой они параллельны. Коллинеарные векторы всегда компланарны, но не все компланарные векторы коллинеарны.
11°. Операции над векторами. Свойства операции над векторами. Суммой векторов a и b называется такой третий вектор c, что при совмещенных началах этих трех векторов, векторы a и b служат сторонами параллелограмма, а вектор c - его диагональю
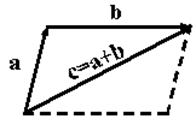
Сложение векторов в соответствии см. рисунком называется сложением по правилу параллелограмма. Однако бывает более удобным использовать для сложения правило треугольника, которое становится ясным из следующего рисунка. Из того же рисунка видно, что результаты сложения по правилу параллелограмма и по правилу треугольника одинаковы.
Свойства сложения векторов. 1о. 2о. 3о. 4о. Для каждого вектора Если Произведением вектора векторы
Произведение вектора на число 0 есть нулевой вектор. Пишут: Свойства умножения вектора на число.
Вычитание векторов. 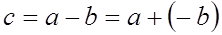 , т.е. , т.е.
12. Понятие линейной зависимости векторов. Линейно независимые векторы. Необходимое и достаточное условие коллинеарности двух векторов. Необходимое и достаточное условие компланарности трех векторов. Говорят, что векторы Если же равенство Лемма. Векторы Необходимое и достаточное условие коллинеарности двух ненулевых векторов Теорема. Для того, чтобы два ненулевых вектора Доказательство. Необходимость. Пусть векторы Достаточность. Пусть векторное произведение Необходимое и достаточное условие компланарности трёх векторов Теорема. Для того чтобы ненулевые векторы a,b и c были компланарны, необходимо и достаточно, чтобы их смешанное произведение равнялось нулю.(a1, a2, a3 – комплонарны ó a1, a2, a3 - ЛЗВ)
Доказательство. Необходимость. Пусть векторы a,b,c компланарны. Тогда их можно поместить в одной плоскости, и вектор Достаточность. Пусть 1) 2)
13°. Теорема о разложении вектора на плоскости по двум неколлинеарным векторам. Пусть дана π-плоскость, e1,e2 – ЛЗВ, тогда любой вектор а в плоскости π, можно представить в виде линейной комбинации: a = xe1 +ye2, причем данное представление единсивенное. Пусть Вектор Вектор
|
|||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 641; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.43.109 (0.006 с.) |

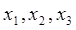 имеет вид
имеет вид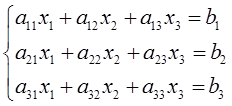 (4)
(4)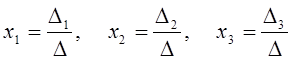 , (5)
, (5)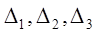 - определители третьего порядка, получаемые из определителя системы Δ заменой первого, второго или третьего столбца соответственно столбцом свободных членов
- определители третьего порядка, получаемые из определителя системы Δ заменой первого, второго или третьего столбца соответственно столбцом свободных членов 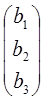 .
.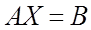 , где
, где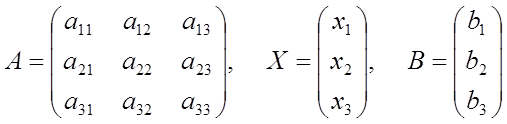 .
.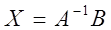 , (6)
, (6)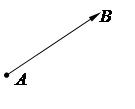
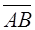 и
и 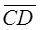 называются сонаправленными, (обозначается
называются сонаправленными, (обозначается 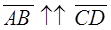 ), если они лежат на параллельных прямых и направлены в одну сторону.
), если они лежат на параллельных прямых и направлены в одну сторону.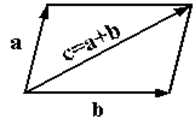
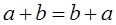 .
.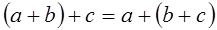 .
.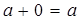 , т.к.
, т.к.  .
.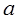
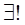 вектор, называемый вектором, противоположным
вектор, называемый вектором, противоположным 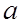 , такой, что
, такой, что 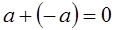 .
.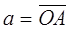 , то через
, то через 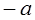 обозначим
обозначим 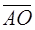 . Тогда
. Тогда 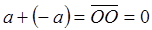 .
.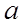 на число
на число 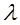
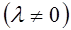 называется вектор
называется вектор 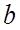 , удовлетворяющий следующим условиям:
, удовлетворяющий следующим условиям: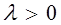 и противоположно направлены, если
и противоположно направлены, если 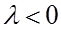 ;
;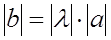 .
.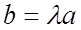 .
.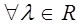 и
и 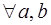
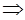
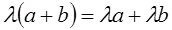 .
.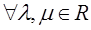 и
и 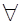 вектора
вектора 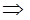
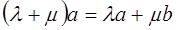 .
.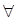 вектора
вектора 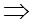
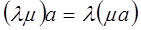 .
.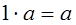 .
.
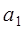 ,
, 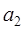 ,
, 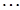 ,
, 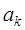 линейно зависимы, если существуют числа
линейно зависимы, если существуют числа 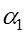 ,
, 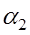 ,
, 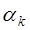 , не все равные нулю и такие, что линейная комбинация
, не все равные нулю и такие, что линейная комбинация 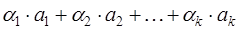 равна нулевому элементу
равна нулевому элементу 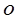 линейного пространства
линейного пространства 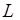 .
.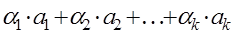
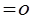 возможно только при условии
возможно только при условии 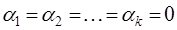 , то векторы
, то векторы 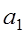 ,
, 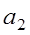 ,
, 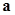 и
и  были коллинеарны, необходимо и достаточно, чтобы их векторное произведение было бы равно нулю.(a| | b ó a,b - ЛЗВ)
были коллинеарны, необходимо и достаточно, чтобы их векторное произведение было бы равно нулю.(a| | b ó a,b - ЛЗВ)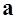 и
и 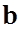 коллинеарны, тогда они лежат на одной прямой, следовательно,
коллинеарны, тогда они лежат на одной прямой, следовательно, 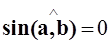 =>
=> 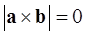 . Значит,
. Значит, 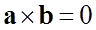
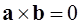 . Так как
. Так как 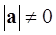 ,
, 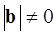 , то значит
, то значит 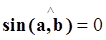 , т.е.
, т.е. 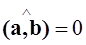 или
или 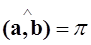 , а это означает, что векторы
, а это означает, что векторы 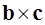 окажется перпендикулярным векторy a, следовательно, их скалярное произведение равно нулю, т.е.
окажется перпендикулярным векторy a, следовательно, их скалярное произведение равно нулю, т.е. 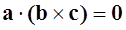 .
. . Так как векторы ненулевые, то может быть:
. Так как векторы ненулевые, то может быть: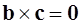 , тогда
, тогда 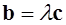 , следовательно, векторы a,b,c можно поместить в одной плоскости, т.е. они компланарны;
, следовательно, векторы a,b,c можно поместить в одной плоскости, т.е. они компланарны;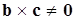 , но
, но 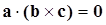 =>
=> 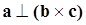 . Это значит, что вектор a лежит в одной плоскости с векторами b и c.
. Это значит, что вектор a лежит в одной плоскости с векторами b и c.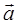 и
и 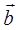 - данные неколлинеарные векторы. Докажем сначала, что любой вектор
- данные неколлинеарные векторы. Докажем сначала, что любой вектор 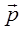 можно разложить по векторам
можно разложить по векторам 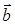 . Возможны два случая.
. Возможны два случая.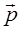 коллинеарен одному из векторов
коллинеарен одному из векторов 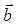 , например вектору
, например вектору 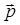 . В этом случае по лемме о коллинеарных векторах вектор
. В этом случае по лемме о коллинеарных векторах вектор 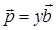 , где
, где 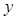 - некоторое число, и, следовательно,
- некоторое число, и, следовательно, 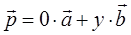 , т.е. вектор
, т.е. вектор 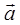 и
и 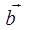 .
.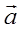 , ни вектору
, ни вектору 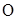 и отложим от нее векторы
и отложим от нее векторы 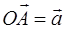 ,
, 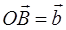 ,
, 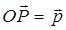 (рис.11). Через точку P проведем прямую, параллельную прямой
(рис.11). Через точку P проведем прямую, параллельную прямой 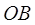 , и обозначим через A1 точку пересечения этой прямой с прямой OA. По правилу треугольника
, и обозначим через A1 точку пересечения этой прямой с прямой OA. По правилу треугольника 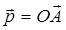 1
1 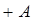 1
1 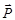 . Но векторы
. Но векторы 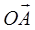 1 и
1 и 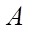 1
1  и
и  ? Такие, что
? Такие, что 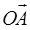 1=
1= 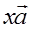 ,A1
,A1 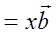 . Следовательно,
. Следовательно, 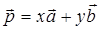 , т.е. вектор
, т.е. вектор 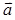 и
и 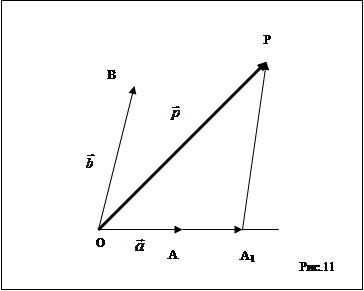 Докажем теперь, что коэффициенты
Докажем теперь, что коэффициенты 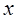 и
и 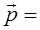 х1
х1 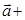 у1
у1 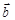 . Вычитая второе равенство из первого и используя правила действий над векторами, получаем
. Вычитая второе равенство из первого и используя правила действий над векторами, получаем 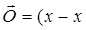 1)
1) 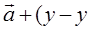 1). Это равенство можно выполнять только в том случае, когда коэффиценты
1). Это равенство можно выполнять только в том случае, когда коэффиценты 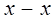 1 и
1 и 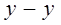 1 равны нулю. В самом деле, если предложить, например, что х-х1
1 равны нулю. В самом деле, если предложить, например, что х-х1 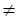 0, то из полученного равенства найдем
0, то из полученного равенства найдем 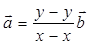 , а значит, векторы
, а значит, векторы 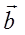 коллинеарны. Но это противоречие условию теоремы. Следовательно, х-х1=0 и у-у1=0, откуда х=х1 и у=у1. Это и означает, что коэффиценты разложения вектора
коллинеарны. Но это противоречие условию теоремы. Следовательно, х-х1=0 и у-у1=0, откуда х=х1 и у=у1. Это и означает, что коэффиценты разложения вектора 


