
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейные операции над геометрич.векторами.Содержание книги Поиск на нашем сайте
Линейные операции над геометрич.векторами. К ним относят: сложение, вычитание, умножение на число. Сложение. а+b=ОВ строим треугольник,начало одного вектора совмещая с концом другого(Правило треугольника.). а+b=с строим параллелограмм,совмещая концы векторов. Полученная большая диагональ-сумма этих векторов Разность. См.правило треугольника,только в этом случае совмещаем концы векторов Произведение на число(скаляр). Это вектор лямда на а,равный длине |лямда| на |а|. это произведение коллинеарно вектору а,имеет направление вектора а если лямда больше нуля и минус а если лямда меньше нуля. Отсюда следуют свойства: каждый вектор равен произведению его модуля на орт и если b=лямда на а,то b||a,наоборот,если b||a,то при некотором лямда верно b=лямда на a. Коллинеарные векторы отдельно см в предидущем впоросе. 4. Деление отрезка в заданном отношении.
Т.к корд.равны значит то,что равные векторы имеют равные координаты. Если лямда равна единице то АМ=МВ, если лямда равна нулю,то А и М совпадают, если лямда меньше нуля то М делит АВ внешним образом (точка лежит вне отрезка). Понятие радиус-вектора. Разложение произвольного вектора по ортам коорд осей на плоскости и в пространстве. Радиус вектор - вектор, задающий положения точки в пространстве относительно некоторой заранее фиксированной точки, называемой началом координат. Для произвольной точки в пространстве, радиус-вектор — это вектор, идущий из начала координат в эту точку
Выделем на корд.осях единичные векторы: I,j,k. Выберем произв.вектор а пространства и совместим его начало с началом коорд: а=ОМ. Найдем проекции вектора а на коорд оси. Проведем через конец вектора ОМ плоскочти,параллельные координатным плоскостям. Точки пересеч этих плоскостей с осями обозначим через М1,М2,М3. Получим прямоуг парал-пед,одной из диагоналей которого является вектор ОМ. По опред суммы векторв находим: а=ОМ1+M1N+NM. А так как M1N=OM2, NM=OM3,то а=ОМ1+ОМ2+ОМ3. ОМ1=|ОМ1|i и тд. Обозначим проекции вектора на оси|ОМ1|=аy итд. В итоге получается: a=ax на i+ay на j+ az на k. Действия с геометрическими векторами в коорд форме. Признак коолинеарности векторов. Линейные операции. При сложении (вычитании) векторов их одноименные координаты складываются (вычитаются). а+b=(ах+bx; ay+by; az+bz). При умножении вектора на скаляр координаты вектора умножаются на этот скаляр. ᵡ а= (ᵡаx; ᵡay;ᵡaz)
Равенство векторов: а и b равны тогда и только тогда,когда выполняется равенство: ax=bx; ay=by; az=bz. Координаты вектора: координаты вектора равны разностям соответсвующих координат его конца и начала. Коллинеарность векторов: Проекции коллинеарных векторов пропорциональны,и наоборот, векторы, имеющие пропорциональные координаты коллинеарны. Док-во: ax на i + ay на j + az на k = лямда (bx на i + by на j + bz на k) Отсюда: ax= лямда на bx итд. Т.е ax\bx=ay\by=az\bz Скалярное произведение геометрических векторов и его св-ва. Признак ортогональности векторов. Скалярное произведение двух ненулевых векторов а и b это число,равное произведению длин этих векторов на косинус угла между ними Св-ва скалярного произведения: Переместительное: ab=ba,т.к |a| |b| =|b| |a| и cos (ab)= cos (ba) Сочетательное: (лямда на а) на b = лямда на (a на b) Распределительное: a (b+c)=ab+ac Скалярный квадрат вектора равен квадрату его длины: a в квадрате = |a|в квадрате; в частности i=j=k=1 i,j,k –в квдрате Если векторы а и b (ненулевые) взаимно перпендикулярны(ортогональны),то их скалярное произведение равно нулю, справедливо и обратное утверждение. Вычисление скалярного произведения векторов через их координаты, длина вектора, расстояние между двумя точками. Вычисление косинуса угла между двумя векторами Скалярное произведение векторов равно сумме произведений их одноименных координат. Дов-во: а=ах на i+ ay на j+ az на k b=bx на i+by на j+ bz на k Найдем скалярное произведение перемножая как многочлены. По таблице скалярного произведения векторов: i на i=1, i на j=0, I на k=0 и тд. В итоге у нас останется: аb=axbx+ayby+azbz Длина вектора: это длина отрезка и обозначается как |AB|. Вектор длина которого равна 1 – единичный вектор. Обознач как е. Если рассматривать АВ,где A(x1) и B(x2) точки на корд прямой,то расстояние АВ=|х2-х1| Расстояние между двумя точками: на плоскости: АВ= (y1-y2)²+(x1-x2)² все под корнем. Пусть в системе корд заданы две точки А(х1,у1) и В(х2,у2). Из этих точек опусти перпендикуляры на ось Ох,из точки В на Оу. |АВ|=АМ²+ВМ² все под корнем. В пространстве: тоже самое плюс z. Косинус угла между векторами: cos α=AB на AC\ |AB| на |AC| или ab\ |a| |b|.
Окружность и ее уравнение Окружностью называется множество точек равноотдаленных от центра. Простейшей кривой второго порядка является окружность. Окружностью радиуса R с центром в точке M0 называется множество всех точек М плоскости,удовлетворяющих условиюМ0М=R. Пусть М0 в Оху имеет координаты (х0,у0), а М(х,у)-произв.точка окружности. Тогда из равенства написанного выше получим: (х-а)² + (у – в)² = R² -каноническое уравнение окружности с R(a;b) В частности полагая а=0 в=о,получим уравнение окружности с центром в начале координат x²+ y²= R² Уравнение окружности (х-а)² + (у – в)² = R² после несложны преобразований примет вид x²+y²-2ax-2by+a²+b²-R²=0 Система линейных уравнений и ее решение. Различные формы записи системы линейных уравнений. Определения однородной, неоднородной, совместной, несовместной, определенной и неопределенной систем Система линейных алгебраических уравнений это систем вида: а11х1+а12х2+а1nхn=b1(первая строка,нижние по аналогии). Подлежат нахождению числа Xn. bi-свободный член. Такую систему удобно записывать в матричном виде: А×Х=В. Х-вектор столбец из неизвестных х. В-вектор столбец из свободных членов b. А-матрица коэффициентов системы,называемая основной матрицей. Расширенная матрица системы-матрица А, дополненная столбцом свободныз членов. Решением системы называется n значений неизвестных х1=с1,х2=с2 и тд. Решение можно записать в виде матрицы-столбца С. Система уравнений называется совместной если она имеет хотя бы одно решение, несовместной если не имеет решений. Совместная система называется определенной если она имеет единственное решение и неопределенной если более одного решения. Системы эквиваленты если имею одно и то же общее решение. Система линейных уравнений называется однородной если все свободные члены равны нулю. Формулы Крамера xi=Δi\Δ. Δ1 получена из Δ путем замены первого столбца коэффициентов столбцом из свободных членов. Записываем матричное равенство в виде: (х1)=1\Δ (А11 А12 А13) × (b1). записана первая строка,нижние по аналогии. Далее внесем определитель и свободные члены в основную матрицу. Отсюда следует: х1=А11b1+A12b2+… (нижние строки по аналогии). Но А11b1+A12b2+… есть разложение определителя по элементам первого столбца. Значит см.выше. Теорема Кронекера-Капелли. Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг расширенной матрицы системы равен рангу основной матрицы. Если ранг совместной системы равен числу неизвестных, то система имеет единственное решение. Если ранг совместной системы меньше числа неизвестных, то система имеет бесчисленное множество решений Правило решения произвольной системы уравнений. Найти ранг основной и расширенной матриц,если они не равны,то система несовместна(нет решений). Найти какой-либо базисный минор порядка r. Взять r уравнений из коэффициентов которых составлен базисный минор(остальные отбросить). Коэффициенты которые входят в базисный минор-главные,записываются слева, остальные переносятся в правые части уравнений(свободные). Далее найти выражения главных неизвестных через свободные. Получается общее решение системы. Затем придавая свободным неизвестным произвольные значения получим соответствующие значения главных неизвестных(частные решения исходной системы).
36 ) Условия определенности и неопределенности систем линейных уравнений. Система уравнение называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет ни одного решения. Совместная система называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения. В последнем случае каждое ее решение называется частным решением системы. Совокупность всех частных решений называется общим решением. Решить систему - это значит выяснить, совместна она или несовместна. Если система совместна, найти ее общее решение. Две системы называются эквивалентными( равносильными), если они имеют одно и то же общее решение. Другими словами, системы эквивалентны, если каждое решение одной из них является решением другой, и наоборот. Эквивалентные системы получаются, в частности, при элементарных преобразованиях системы при условии, что преобразования выполняются лишь над строками матрицы. Система линейных уравнений называется однородной, если все свободные члены равны нулю. Однородная система всегда совместна, т.к х1=х2….=хn=0 является решением системы. Это решение называется нулевым или тривиальным. 37) Решение систем линейных уравнений методом Гаусса. Пусть дана система уравнений: 1)a11x1+a12x2+….a1nXn=b1 a21x1+a22x2+….a2nXn=b2 …………………………… am1X1+am2X2+…..amnXn=bn
Процесс решения по методу Гаусса состоит из двух этапов. На первом этапе(прямой ход) система приводится к ступенчатому (в частности, треугольному) виду. Приведенная ниже система имеет ступенчатый вид: a11x1+a12x2+….+a1kXk+….a1nXn=b1 a22x2+….+a2kxk+…. a2nXn=b2 ……………………… akkXk+….aknXn=bk Прямой ход. Будем считать, что элемент а11 не равен 0(если а11=0, то первым в системе запишем уравнение, котором коэффициент при x1отличен от нуля) Преобразуем систему, исключив неизвестное х1 во всех уравнениях, кроме первого(используя элементарные преобразования системы). Для этого умножим обе части уравнение на –а21/а11 и сложим почленно со вторым уравнением системы. Затем умножим обе части первого уравнения на –а31/а11 и сложим с третьим уравнением системы. Продолжаем этот процесс, получим эквивалентную систему: 2)a11x1+a12x2+….a1nXn=b1 a22x2+….a2nXn=b2 …………………………… am2X2+…..amnXn=bm Аналогичным образом, считая главным элементом а22 не =0, исключим неизвестное х2 из всех уравнений системы, кроме первого и второго, и так далее. Продолжаем этот процесс, пока это возможно. Если в процессе приведения системы(номер 1) к ступенчатому виду появятся нулевые уравнения,т.е равенства вида 0=0, их отбрасывают.
Обратный ход. Заключается в решении ступенчатой системы. Ступенчатая система уравнений, вообще говоря, имеет бесчисленное множество решений. В последнем уравнении этой системы выражаем первое неизвестное Xk через остальные неизвестные (Хк+1,…..Xn). Затем подставляем значение Xk в предпоследнее уравнение системы и выражаем Xk-1 через (Xk+1,….Xn); затем находим Xk-2,……х1. Придавая свободным неизвестным (Xk+1,….Xn) произвольные значения, получим бесчисленное множество решений системы. Замечания: 1) Если ступенчатая система оказывается треугольной, т.е k=n, то исходная система имеет единственное решение. 2) На практике удобнее работать не с системой 1, а с расширенной ее матрицей, выполняя все элементарные преобразования над ее строками.
38) Теорема о совместности однородной системы линейных уравнений. Пусть дана система линейных однородных уравнений: а11х1+а12х2+….+а1nXn=0 а12х1+а22х2+….+а2nXn=0 ……………………………. Am1x1+am2x2+……+amnXn=0 Однородная система всегда совместна,она имеет нулевое(тривиальное) решение х1=х2=….=хn=0 Теорема. Для того, чтобы система однородных уравнений имела ненулевые решения, необходимо и достаточно, чтобы ранг r ее основной матрицы был меньше числа n неизвестных, т.е r<n Необходимость. Т.к ранг не может превосходить размера матрицы, то, очевидно, r< или = n. Пусть r=n. Тогда один из миноров размера n x n отличен от нуля. Поэтому соответствующая система линейных уравнений имеет единственное решение: xi= ∆i/∆=0, ∆i=0, ∆ не =0. Значит, других, кроме тривиальных, решений нет. Если есть нетривиальное решение, то r<n. Достаточность. Пусть r<n. Тогда однородная система, будучи совместной, является неопределенной. Значит, она имеет бесчисленное множество решений, т.е имеет и ненулевые решения.
39) Теорема о существовании ненулевых решений однородных систем линейных уравнений. Теорема. Для того, чтобы однородная система n линейных уравнений с n неизвестными имела ненулевые решения, необходимо и достаточно, чтобы ее определитель ∆был равен нулю, т.е ∆=0 Если система имеет ненулевые решения, то ∆=0. Ибо при ∆ не равно 0 система имеет только единственное, нулевое решение. Если же ∆=0, то ранг r основной матрицы системы меньше числа неизвестных, т.е r<n/ И, значит, система имеет бесконечное множество(ненулевых) решений. 40) Линейное(векторное) пространство. Пространство Rⁿ и линейные операции в этом пространстве. Векторное (линейное) пространство - математическое понятие, обобщающее понятие совокупности всех (свободных) векторов обычного трехмерного пространства. Векторным пространством (над полем R или C) называют множество L, состоящее из элементов любой природы (называемых векторами), в котором определены операции сложения элементов и умножения элементов на действительные (комплексные) числа, удовлетворяющие следующим условиям: 1) x + y = y + x (коммутативность сложения); 2) (x + y) + z = x + (y + z) (ассоциативность сложения); 3) имеется нулевой вектор 0 (или нуль-вектор), удовлетворяющий условию x + 0 = x для любого вектора x;
4) для любого вектора x существует противоположный ему вектор y такой, что x + y = 0; 5) 1∙x = x; 6) α(βx) = (αβ)x (ассоциативность умножения); 7) (α + β)x = αx + βx (дистрибутивность относительно числового множителя); 8) α(x + y) = αx + αy (дистрибутивность относительно векторного множителя). Векторное пространство называют. n-мерным (или имеет «размерность n»), если в нём существуют n линейно независимых элементов e1, e2,...en, а любые n+1 элементов линейно зависимы. Векторное пространство называют бесконечномерным, если в нём для любого натурального n существует n линейно независимых векторов. Любые n линейно независимых векторов n-мерного векторного пространства образуют базис этого пространства. Если e1, e2,...en - базис векторного пространства, то любой вектор x этого пространства может быть представлен единственным образом в виде линейной комбинации базисных векторов: x = α1e1 + α2e2 +... + αnen. При этом числа α1, α2,...,αn называют координатами вектора x в данном базисе. Множество всех векторов 3-мерного пространства образует векторное пространство. Более сложным примером может служить так называемое n-мерное векторное пространство. Векторами этого пространства являются упорядоченные системы из n действительных чисел (λ1, λ2,..., λn). Сумма двух векторов и произведение на число определяются соотношениями: (λ1, λ2,..., λn) + (μ1, μ2,..., μn) = = (λ1 + μ1, λ2 + μ2,..., λn + μn), α∙(λ1, λ2,..., λn) = (α∙λ1, α∙λ2,..., α∙λn). Базисом в этом пространстве может служить, например, следующая система из n векторов: e1 = (1, 0,..., 0), e2 = (0, 1,..., 0),...en = (0, 0,..., 1).
41) Скалярное произведение n-мерных векторов. Неравенство Коши-Буняковского. Косинус угла между m-мерными векторами. Скалярным произведением двух векторов называется число, равное произведению модулей этих векторов на косинус угла между ними. Скалярное произведение векторов а, b обозначается символом ab(две черточки сверху) (порядок записи сомножителей безразличен, то есть ab=ba) Угол (фи) между векторами: А=(x1;y1;z1) B=(x2;y2;z2) Нера́венство Коши́ — Буняко́вского Для любых элементов и линейного пространства со скалярным произведением выполняется неравенство. |(x,y)|<или =||x||*||y|| связывает норму и скалярное произведение векторов в линейном пространстве. Это неравенство эквивалентно неравенству треугольника для нормы в пространстве со скалярным произведением. Пусть дано линейное пространство L со скалярным произведением (x;y). Пусть||x|| — норма, порождённая скалярным произведением, то есть ||x||=(x;x)(все под корнем). Тогда для любых х,у принадлежит L имеем: |(x,y)|<или =||x||*||y|| причём равенство достигается тогда и только тогда, когда векторы x и y пропорциональны (коллинеарны). В пространстве комплекснозначных квадратично суммируемых последовательностей i² неравенство Коши — Буняковского имеет вид:
В пространстве комплексных квадратично интегрируемых функций
Косинус угла между векторами находят из их скалярного произведения. Сумма произведения соответствующих координат вектора равна произведению их длин на косинус угла между ними. 42) Определение линейно зависимых и независимых векторов. Критерий линейной зависимости и независимости векторов в пространстве Rⁿ. Пусть имеем векторное пространство V и систему векторов A={ Определение 1. Система векторов A называется линейно-независимой, если только тривиальная линейная комбинация векторов системы равна Определение 2. система векторов A называется линейно-зависимой, если существует хотя бы одна нетривиальная линейная комбинация, равная Критерий линейной зависимости векторов: Для того чтобы векторы Размерность линейного пространства Линейное пространство V называется n-мерным (имеет размерность n), если в нем: 1) существует n линейно независимых векторов; 2) любая система n + 1 векторов линейно зависима. Базис линейного пространства. Примеры базисов в R в степени n. Базисом линейного пространства L называется система элементов принадлежащих L, удовлетворяющая двум условиям: 1) система линейно независима. 2) Любой элемент L линейно выражается через базисные (т.е. является линейной комбинацией элементов) Базис в пространстве R в степени n (канонический базис). Примеры: Базисом в пространстве называются три некомпланарных вектора, взятые в определённом порядке. Эти векторы называются базисными. Подпространство линейного пространства. Линейная оболочка системы векторов. Сумма и пересечение подпространств. Примеры подпространств. Подпространство. Алгебраическое определение: Линейное подпространство или векторное подпространство ― непустое подмножество K линейного пространства L такое, что K само является линейным пространством по отношению к определенным в L действиям сложения и умножения на скаляр. Множество всех подпространств обычно обозначают как Lat(L). Чтобы подмножество было подпространством, необходимо и достаточно, чтобы: -Нейтральный элемент ɵ принадлежит К -для всякого вектора х принадлежит К, вектор αх также принадлежал K, при любом α принадлежит L; -для всяких векторов x,y принадлежит К, вектор x+y также принадлежал K. В частности, пространство, состоящее из одного элемента {θ}, является подпространством любого пространства; любое пространство является само себе подпространством. Подпространства, не совпадающие с этими двумя, называют собственными или нетривиальными. Линейная оболочка £(Х) подмножества X линейного пространства L — пересечение всех подпространств L, содержащих X. Линейная оболочка является подпространством L. Линейная оболочка также называется подпространством, порожденным X. Линейная оболочка £(Х) состоит из всевозможных линейных комбинаций различных конечных подсистем элементов из X. В частности, если X — конечное множество, то £(Х) состоит из всех линейных комбинаций элементов X. Свойства подпространств. Пересечение любого семейства подпространств — снова подпространство; Сумма конечного семейства подпространств — снова подпространство. Сумма подпространств определяется как множество, содержащее всевозможные суммы элементов Ki: Линейные операторы. Основные понятия. Определение. Если каждому элементу ᵡ из линейного постранства L ставится в соответствие единственный элемент «y» из линейного постранства M, то говорят, что задан оператор, действующий из постранства L в пространство M (или оператор, действующий в пространстве L, если L совпадает с M). Результат действия оператора A на элемент ᵡ обозначают: у=А(х). Над у,х и лямда знаки вектора. Если элементы ᵡ и у связаны соотношением у=А(х), то у называют образом ᵡ; а ᵡ — прообразом у. Множество элементов пространства L, для которых определено действие оператора A, называют областью определения оператора A и обозначают D(A). Множество элементов пространства M, которые являются образами элементов из области определения D(A) оператора A, называют образом оператора A и обозначают Im(A). Если у=А(х), то х принадлжежит D(A), y принадлжежит Im(A). Ядром оператора называется множество элементов линейного пространства L, образом которых является нулевой элемент. Ядро оператора обозначают Ker(A). Сложение комплексных чисел. Суммой двух комплексных чисел z1=x1+iy1 и z2=x2+iy2 называется комплексное число, определяемое равенством: z1+z2=(x1+x2)+i(y1+y2) Сложение комплексных чисел обладает переместительным(коммутативным) и сочетательным(ассоциативным) свойствами: z1+z2=z2+z1 (z1+z2)+z3=z1+(z2+z3) Из определения следует, что геометрически комплексные числа складываются как векторы. Деление комплексных чисел. Деление определяется как действие, обратное умножению. Частным двух комплексных чисел z1 и z2 не =0 называется комплексное число z, которое, будучи умноженным на z2, дает число z1. При делении комплексных чисел их модули, соответственно, делятся, а аргументы, соответственно, вычитаются. Сложение комплексных чисел. Суммой двух комплексных чисел z1=x1+iy1 и z2=x2+iy2 называется комплексное число, определяемое равенством: z1+z2=(x1+x2)+i(y1+y2) Сложение комплексных чисел обладает переместительным(коммутативным) и сочетательным(ассоциативным) свойствами: z1+z2=z2+z1 (z1+z2)+z3=z1+(z2+z3) Из определения следует, что геометрически комплексные числа складываются как векторы. Деление комплексных чисел. Деление определяется как действие, обратное умножению. Частным двух комплексных чисел z1 и z2 не =0 называется комплексное число z, которое, будучи умноженным на z2, дает число z1. При делении комплексных чисел их модули, соответственно, делятся, а аргументы, соответственно, вычитаются. Доказательство. Критерий положительной определённости квадратичной формы. Для положительной определённости квадратичной формы необходимо и достаточно, чтобы главные миноры её матрицы были положительны.
1. «Необходимо.» Имеется положительно определённая квадратичная форма. j-ый диагональный элемент положителен, так как k>0 в том числе и для вектора со всеми нулевыми координатами, кроме j-ой. При приведении матрицы к каноническому виду не будет нужно переставлять строки, и знаки главных миноров матрицы не изменятся. А в каноническом виде диагональные элементы положительны, и миноры положительны; следовательно,, у положительно определённой квадратичной формы в любом базисе главные миноры матрицы положительны.
2. «Достаточно.» Имеется положительность миноров. Первый минор определяет знак первого диагонального элемента в каноническом виде. Знак отношения Mi+1/Mi определяет знак i+1-ого элемента в диагональном виде. Так получим, что в каноническом виде все элементы на диагонали положительные, то есть квадратичная форма определена положительно. Критерий отрицательной определённости квадратичной формы. Для отрицательной определённости квадратичной формы необходимо и достаточно, чтобы главные миноры чётного порядка её матрицы были положительны, а нечётного порядка — отрицательны. Доказательство сводится к предыдущему случаю, так как матрица A является отрицательно определённой тогда и только тогда, когда матрица − A является положительно определённой. При замене матрицы A на противоположную главные миноры нечётного порядка меняют знак, а главные миноры чётного порядка остаются такими же.
Линейные операции над геометрич.векторами. К ним относят: сложение, вычитание, умножение на число. Сложение. а+b=ОВ строим треугольник,начало одного вектора совмещая с концом другого(Правило треугольника.). а+b=с строим параллелограмм,совмещая концы векторов. Полученная большая диагональ-сумма этих векторов Разность. См.правило треугольника,только в этом случае совмещаем концы векторов Произведение на число(скаляр). Это вектор лямда на а,равный длине |лямда| на |а|. это произведение коллинеарно вектору а,имеет направление вектора а если лямда больше нуля и минус а если лямда меньше нуля. Отсюда следуют свойства: каждый вектор равен произведению его модуля на орт и если b=лямда на а,то b||a,наоборот,если b||a,то при некотором лямда верно b=лямда на a. Коллинеарные векторы отдельно см в предидущем впоросе. 4. Деление отрезка в заданном отношении.
Т.к корд.равны значит то,что равные векторы имеют равные координаты. Если лямда равна единице то АМ=МВ, если лямда равна нулю,то А и М совпадают, если лямда меньше нуля то М делит АВ внешним образом (точка лежит вне отрезка).
|
|||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 371; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.229.207 (0.01 с.) |

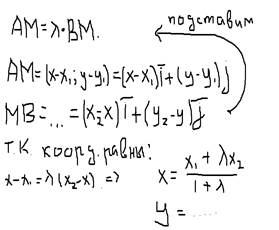

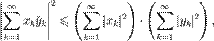
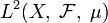 неравенство Коши — Буняковского имеет вид:
неравенство Коши — Буняковского имеет вид: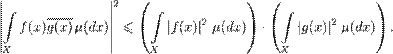
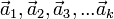 } (система отличается от множества тем, что в ней могут быть одинаковые элементы). Вектор
} (система отличается от множества тем, что в ней могут быть одинаковые элементы). Вектор  называется линейной комбинацией системы векторов A. Если все скаляры α1 = α2 = α3... = αk = 0, то такая комбинация называется тривиальной (простейшей), (и
называется линейной комбинацией системы векторов A. Если все скаляры α1 = α2 = α3... = αk = 0, то такая комбинация называется тривиальной (простейшей), (и  ). Если хотя б один скаляр отличен от 0, то такая комбинация называется нетривиальной
). Если хотя б один скаляр отличен от 0, то такая комбинация называется нетривиальной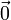 (т.е.
(т.е.  )
)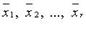 (r > 1) были линейно зависимы, необходимо и достаточно, чтобы хотя бы один из этих векторов являлся линейной комбинацией остальных.
(r > 1) были линейно зависимы, необходимо и достаточно, чтобы хотя бы один из этих векторов являлся линейной комбинацией остальных.


