
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Частные случаи расположения плоскости относительно СК.Содержание книги
Поиск на нашем сайте
Рассмотрим плоскость π: Ах+Ву+Сz+D=0, (О, 1)A=0, 0*x+B*y+C*z+D=0, B*y+C*z+D=0, 2)B=0, A*x+C*z+D=0 ǁ Oy, 3)C=0, A*x+B*y+D=0 ǁ Oz, 4)D=0, A*x+B*y+C*z=0 проходит через начало координат, 5)А=0, В=0, C*z+D=0 ǁ Oxy, 6) A=0, C=0, B*y+D=0 ǁ Oxz, 7) A=0, D=0, B*y+C*z=0 и проходит через начало координат, Ох-лежит в плоскости π, 8)В=0, С=0, A*x+D=0 ǁ Oyz, 9)B=0, D=0, A*x+C*z=0 содержит ось Оу, Оу⊂π, 10) С=0, D=0, A*x+B*y=0, Oz⊂π, 11)A=0, B=0, D=0, C*z=0, z=0,ур-ние плоскости π=Оху, 12)A=0, C=0, D=0, y=0, π=Oxz, 13) B=0, C=0,D=0, x=0, π=Oyz.
39°. Уравнение прямой в пространстве, проходящей через данную точку в данном направлении (каноническое уравнение прямой). Пусть ∆ - нек. прямая,
40°. Параметрическое уравнение прямой в пространстве. Пусть ∆ - нек. прямая,
41°. Уравнение прямой в пространстве, проходящей через две точки. Пусть ∆ - нек. прямая,
42. Взаимное расположение двух плоскостей. Опр: прямая пересечения плоскости с координатной плоскостью наз. следом плоскости на координатной плоскости. Теор: пусть в нек. СК плоскости заданы ур-ниями: 1) плоскости пересекаются ó Док-во.: 1) => Пусть плоскости пересекаются, тогда найдём коор. Плоскость на которой каждая оставляет след, например Oxy (z=0)
43. Взаимное расположение двух прямых в пространстве. Прямые: скрещиваются, пересекаются, параллельны, совпадают. Пусть (О,
44. Взаимное расположение прямой и плоскости. Пусть (О,
2) если 3) если Теор.: Пусть (О, 1) ∆ иπпересек. ó
2) ∆//πó
3) ∆ ᴄπó
45°. Расстояние от точки до плоскости. Пусть (O,
46. Расстояние от точки до прямой в пространстве. Пусть (O,
Расстояние между скрещивающимися прямыми. Пусть (О,
48°. Угол между двумя плоскостями. Угол между двумя плоскостями равен углу между между нормальными векторами к этим плоскостям. Пусть (O,
49°. Угол между двумя прямыми в пространстве. Угол между двумя прямыми равен углу между направляющими векторами. Пусть (О,
Угол между прямой и плоскостью. ∆:
sin
Эллипс и его каноническое уравнение Пусть F 1 и F 2 – некоторые точки плоскости расстояние F 1 F 2 = 2C. Опр: Эллипсом называется фигура состоящая из всех точек плоскости для которых сумма расстояний до двух фиксированных F 1,F 2 есть число постоянно равное 2а, где а>c,F 1, F 2 – называются фокусами. МF 1 + МF 2 =2а. Введем прямоуг. Систему координат. О – середина отрезка F 1 F 2. F 1 (-с,0) F 2 (с,0) M(x,y)-произвольная т. Эллипса. МF 1 = МF 2 = 2a-
Покажем, что всякое уравнение Попробуем найти МF 1 = MF 2 = МF 1 +MF 2 =
График круг
Исследование формы эллипса Пусть х2/а2+у2/b2=1, где b2=a2-c2 F 1 (-c,0) F 2 (c,0) 1)y2=b2/a2(a2-x2) => x2≤a2, |x|≤a x=a, x=-a; X2=a2/b2(b2-y2) => y2≤b2, |y|≤b y=b, y=-b; Все точки эллипса расположены внутри прямоугольника, ограниченного прямыми. 2) M 1 (x1,y1) принадлежит эллипсу, то M 2 (-x1,y1), M 3 (-x1,-y1), M 4 (x1,-y1) принадлежат эллипсу Эллипс симметричен относительно оси О х,О у и начало координат. О(0,0) – центр эллипса. Будем исследовать эллипс только в 1-ой четверти
X≥0, y≥0 y2= y= если х=0, то у=b если х возрастает, то у убывает если х=а, то у=0 А1(-а,0), А2(а,0) вершины эллипса В1(-b,0), B2(b,0) Опр. Прямая, проходящая через фокусы называется факальной осью. Опр. Расстояние от центра эллипса до вершины факальной оси называется большей полуосью (а) Опр. Расстояние от эллипса до вершины факальной оси называется меньшей полуосью.(b-меньшая полуось) Опр. Число равное отношению расстояния между фокусами к расстоянию между вершинами факальной оси наз. эксцентриситетом (степень сжатия окружности из которой получится эллипс) ε<1. Опр. Отрезок, соединяющий точку эллипса сфокусам называется факальным радиусом (МF 1,MF 2) МF 1 =a+(c/a)x=a+εx MF 2 =a-(c/a)x=a+εx Опр. Длина перпендикуляра восстановленного из фокуса до пересечения с эллипсом наз. Факальным араметром Р. Факальный параметр p=b2/a Оптическоесв-во эллипса X2/9+y2/25=1 c2=16 c=4; x’=y, y’=x. F1(-4,0)F2(4,0) X’2/25+y’2/9=1 b2=a2-c2
|
||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 371; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.147.37 (0.01 с.) |

 ,
,  ,
,  ). Утверждение:
). Утверждение:  (
(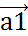 ,
,  ,
,  )ǁ π: Ах+Ву+Сz+D=0 если а1*А+а2*B+а3*С=0, при этом Р1(х1,у1,z1),
)ǁ π: Ах+Ву+Сz+D=0 если а1*А+а2*B+а3*С=0, при этом Р1(х1,у1,z1), 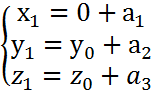 , Р1 ϵ π ⟹
, Р1 ϵ π ⟹  (1,0,0)ǁπǁOx.
(1,0,0)ǁπǁOx. Є ∆,
Є ∆,  ) – аффинный репер,
) – аффинный репер,  ,
,  , MЄ ∆ - произвольн. точка., M(x,y,z),
, MЄ ∆ - произвольн. точка., M(x,y,z),  //
//  ,
,  ,
,  – каноническое ур-ние прямой.
– каноническое ур-ние прямой. , MЄ ∆ - произвольн. точка., M(x,y,z),
, MЄ ∆ - произвольн. точка., M(x,y,z),  , r(x,y,z),
, r(x,y,z), 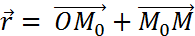 ,
,  – параметрич. ур-ние прямой в векторной форме, (x, y, z)=
– параметрич. ур-ние прямой в векторной форме, (x, y, z)= 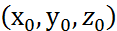 +
+  ,
, ,
, 
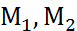 Є ∆,
Є ∆, 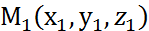 ,
,  , MЄ ∆ - произвольн. точка., M(x,y,z),
, MЄ ∆ - произвольн. точка., M(x,y,z),  – напр. вектор.
– напр. вектор.  - ур-ние прямой, проходящей через две точки.
- ур-ние прямой, проходящей через две точки. , тогда:
, тогда: ; 2)
; 2)  ó
ó  ; 3)
; 3)  ó
ó  .
. прямые пересекаются (
прямые пересекаются ( ) 2) =>
) 2) =>  тогда
тогда  нет решений (
нет решений ( СЛУ имеет бесконечное множество решений.
СЛУ имеет бесконечное множество решений. :
: 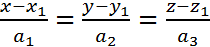 ;
;  :
:  ; Теор.: Пусть
; Теор.: Пусть  – прямые, заданные каноническим ур-нием, тогда: 1)
– прямые, заданные каноническим ур-нием, тогда: 1)  ó
ó  - некомпланарные
- некомпланарные  2)
2)  пересек. ó
пересек. ó  ó
ó  ; 4)
; 4)  ó
ó 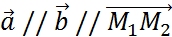
 α = -
α = -  . 1)Если
. 1)Если  = -
= -  , значит прямая и плоскость пересекаются (единственная общая точка);
, значит прямая и плоскость пересекаются (единственная общая точка); , а
, а  ≠ 0; то 0 × α = -
≠ 0; то 0 × α = -  , тогда 0×α=0, α – произвольное число. Ур-ние имеет бесконечное множество решений, значит прямая лежит в плоскости.
, тогда 0×α=0, α – произвольное число. Ур-ние имеет бесконечное множество решений, значит прямая лежит в плоскости. ;
; ;
; ) π: Ax+By+Cz+D=0; P – не принадлежит плоскости. P
) π: Ax+By+Cz+D=0; P – не принадлежит плоскости. P  , MЄπ, M
, MЄπ, M  , PN
, PN  π,
π,  , |
, |  |= |
|= |  |× cos(
|× cos( ) =
) =  =
=  =
= 
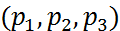 , ρ(P,∆) = PN, PN – высота параллелепипеда, построенного на векторах
, ρ(P,∆) = PN, PN – высота параллелепипеда, построенного на векторах  и
и  =
= 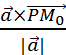 =
= 
 =
=  =
= 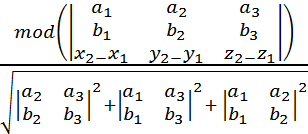
 ,
,  ,
,  (
( )= |
)= |  |=
|=  =
= 
 =
= 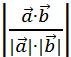 =
= 
 =90-
=90-  (
( );
);  | =
| =  ;
;  =
= 

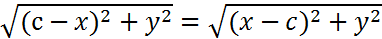
 +
+  =2a
=2a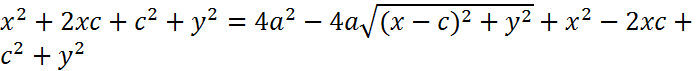
 возведем и перегруппируем
возведем и перегруппируем

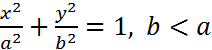
 определяет эллипс. Пусть точка М(х0,у0)-точка удовлетворяющая урв-ию
определяет эллипс. Пусть точка М(х0,у0)-точка удовлетворяющая урв-ию

 =2a
=2a (a2-x2)
(a2-x2) , Х изменяется от О до a
, Х изменяется от О до a


