
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Поверхности второго порядка, заданные общим уравнением.Содержание книги
Поиск на нашем сайте Опр. Уравнение вида
где (т.е. хотя бы один коэффициент Опр. Фигура, которая в некоторой специально выбранной прямоугольной системе координат может быть задана уравнением (2.1) называется поверхностью второго порядка. Пример. Пусть фигура задана уравнением
Если (2.2) подставить в уравнение (2.1), и наложить условие, что коэффициенты при слагаемых где
а углы в системе (2.2) находятся из решения системы:
Рассмотрим случаи. I) Пусть
Обозначая новую систему координат Возможны следующие случаи: I1. Если I2. Если I3. Если I4. Если I5. Если I6. Если
Бинарные отношения. Бинарным отношением,заданным на множестве А, называется подмножество R≤А²(А×А). Если a и b є А, то aRb(элемент а находится в бинарном отношении R с элем.b). Пусть на множ. А задано бин.отнош.R, тогда,если R=A²,то назыв. универ сальное бинарное отношение,если R=0,то R-пустое бин.отнош.Опр.Б.о.R назыв. 1) рефлексивным,если aRa; 2) симметричным,если aRb→bRa; 3) транзитивным,если aRb, bRc→aRc; 4) антисимметричным, если aRb, bRa→a=b. 70°. Отношение эквивалентности и порядка. Отношение эквивалентности и порядка.Б.о.R наз.отношением эквивалентности,если R-рефлексивно,симметрично и транзитивно. Опр. Пусть R-отнош.экв. аєА.Множество ā={xєA|aRx}назыв. классом эквивалентности элем. а. Теорема:любых два класса эквивалентности либо не пересекаются, либо совпадают. Опред:если на множ.А задано отнош.эквив. ̴,то совокупность всевожможных непересекающихся классов эквив. наз. фактор-множеством(А ̰).Б.о. наз. отнош.частичного порядка,если рефл., антисимм., транзитивно.Элем. a и b-сравнимые,если aRb или bRa, в противном случае они несравнимы.
71°. Алгебраическая операция. Свойства алгебраических операций. Свойства алг.опер. Пусть X-непустое множество. Говорят,что на множестве Х задана алг. опер., если указано правило, по которому двум любым элементам этого множества ставится в соответствие вполне определённый элемент этого множества. Элем.nєX наз. нейтральным, если n◦a=a◦n=a. Алг.опер. наз. ассоциативной, если a◦(b◦c)=(a◦b)◦c.Пусть на Х задана алг.о. Элем. aєX наз.симметричным к bєX, если a◦b=b◦a=n.Алг. о. наз.коммутативной,если a◦b=b◦a. Свойства: 1)если существует n.,то он единственный; 2)симметричный элем- единственный.
72°.Определение группы.Простейшие свойства групп. Непустое множество G наз. группой,если на нём задана алг. опер.,удовл.условиям:G1)◦ -ассоц-на a◦(b◦c)=(a◦b)◦c;G2)сущ-ет nєG; n◦a= a◦n =a;G3)для люб. a◦G сущ. b симметр.эл. a◦b=b◦a=n.G4)Группа наз. коммутата тивной (абелевой), если ◦ -коммут. опер., т.е. a◦b=b◦a. Свойства:1)n-единств-й;2)для люб. a,bєG уравнения ax=b,ya=b – им.единственные решения; 3)обратным элем к произв.(ab)-1=b-1a-1. Группа, на которой задана опер. «сложения»-аддитивная, «умножения»-мультипликативная.
73°. Определение кольца. Простейшие свойства колец. Непустое множество К наз.кольцом,если на нём заданы 2 алг. оп. «+», «*»,для которых выполняются аксиомы:К1)К явл.абелевой группой относит. «+»(проверить G1,G2,G3,G4) К2)опер «*умн.»-ассоц-на, т.е. a*(b*c)=(a*b)*c;К3)умнож.дистрибутивно отностит.оп. сложения,т.е. a*(b+c)=a*b+a*c. Опр: кольцо назыв. коммутативным кольцом, если опер. умн.коммут-на К4)a*b=b*a. Опр: коль цо К наз.кольцом с единицей,если К5) существует nєК n*a=a*n=a. Свойства: 1) кольцо явл.коммутат.гр., значит для него вып-ся все св-ва групп 2) в кольце можно ввести опер. вычитания; 3) если a*0=0*a=0; a*b=0; a 4) если а не является делителем 0, то a*b=a*c→ b=c; 5) (-a)*b=a*(-b)=-(a*b); 6) if K-кольцо с 1,то оно единственно; 7) К(кольцо с обратн. эл.)- группа отн.умнож.
74°.Определение поля.Простейшие свойства поля. Коммутативное кольцо с единицей, в котором все элементы кроме 0 обратимы наз. полем. Вып. усл. (К1-К5). Свойства: 1) для полей верны все св-ва колец К1) К явл.абелевой группой относит. «+»(проверить G1,G2,G3,G4) К2) опер «*умн.»-ассоц-на, т.е. a*(b*c)=(a*b)*c; К3) умнож. дистрибутивно отностит. оп. сложения, т.е. a*(b+c)=a*b+a*c. Опр: кольцо назыв. коммутативным кольцом, если опер. умн.коммут-на К4)a*b=b*a.Опр: кольцо К наз. кольцом с единицей,если К5) существует nєК n*a=a*n=a.; 2) в поле нет делитителей 0; 3)ax=b-единств.реш.,если aǂ0.
Изоморфизмы групп, колец. Группы G1,G2 наз.изоморфными,если существует взаимооднозначное соответствие(биекция)f:G1→G2; f(a◦b)=f(a)*f(b) f-изоморфизм. Опр. Кольцо К1 и К2 наз. изоморфными, если сущ. биекция f:K1→K2; f(a+b)=f(a)+f(b);f(a*b)=f(a)*f(b) C1 Свойства изом.группы: 1)G 2)G 3)G Множество групп разбивается на взаимно непересекающиеся классы изоморфных групп.
76⁰.Построение поля комплексных чисел.Алгебраическая форма комплексного числа. Пусть z1=a1+b1i, z2=a2+b2i принадлежат С, z1=z2,если a1=a2,b1=b2. Опр. Суммой двух элементов z1 и z2єС наз.эл. Опр. Произведением Теорема. Множество С={a+bi|a,bєR} с операциями сложения и умн. явл-ся полем. Зам:каждый ненулевой элемент множества обратим. Опр. Пусть z=a+bi є C Опр. Пусть z=a+bi є C; a=Rez-действит. часть компл.числа;b=Imz-мнимая часть; a+0i – действительные числа; 0+bi – мнимые числа.
77°.Тригонометрическая и экспоненциальная форма записи комплексного числа.Действия над компл. числами в триг.и экспон.форме записи. Рассм.С={a+bi|a,bєR} z=a+bi.Каждому числу z=a+bi можно поставить в соответствие точку с координатами (a,b)в прямоугольной CK.и наоборот –это взаимно однозначное соответствие.
78°.Возведение в степень и извлечение корня n-ой степени из комплексного числа. Опр. z0=1;z1=z;zn=z*z*z… Опр. Z-n=
|
||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 414; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

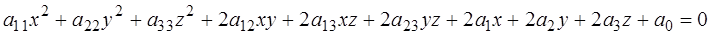 , (2.1)
, (2.1)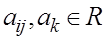 ,
, 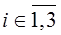 ,
, 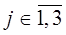 ,
, 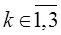 ,
, 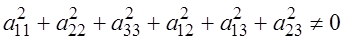
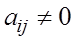 ) называется уравнением второго порядка от трех переменных.
) называется уравнением второго порядка от трех переменных.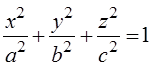 . Здесь
. Здесь  ,
, 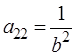 ,
, 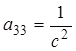 ,
,  , а все остальные коэффициенты равны нулю. Перейдем к новой системе координат по формулам:
, а все остальные коэффициенты равны нулю. Перейдем к новой системе координат по формулам: (2.2)
(2.2)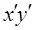 ,
, 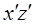 ,
, 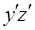 будут равны нулю, то получим уравнение вида
будут равны нулю, то получим уравнение вида 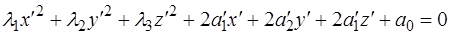 (2.3)
(2.3)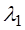 ,
, 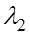 ,
, 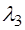 находятся из уравнения:
находятся из уравнения: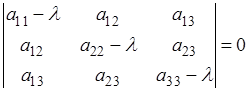 ,
,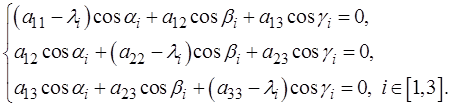
 ,
,  ,
,  . Тогда
. Тогда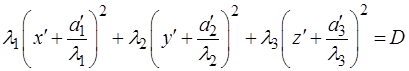 , где
, где 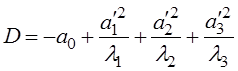 .
.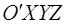 будем иметь
будем иметь  ,
,  ,
, 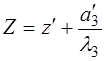 . Теперь имеем
. Теперь имеем 
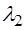 ,
,  одного знака, а
одного знака, а 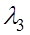 противоположного знака, то фигура, заданная уравнением (2.1) – однополостный гиперболоид.
противоположного знака, то фигура, заданная уравнением (2.1) – однополостный гиперболоид.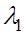 ,
, 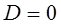 , то фигура, заданная уравнением (2.1) – точка (начало координат, точка
, то фигура, заданная уравнением (2.1) – точка (начало координат, точка 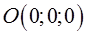 ).
).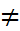 0, b
0, b 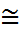 C2 – изоморфно
C2 – изоморфно .
.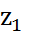 и
и 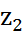 н.
н.  .
.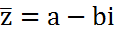 наз.комплексно-сопряж.
наз.комплексно-сопряж.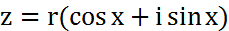 - тригонометрическая форма записи компл.числа.
- тригонометрическая форма записи компл.числа. 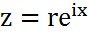 – экспоненциальная форма.
– экспоненциальная форма. 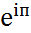 =-1.
=-1. 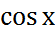 =
=  .
.  .
.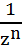 . Формула Муавра:
. Формула Муавра: 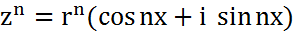 ; Опр. Корнем n-ой степени из числа z наз.число w такое, что wn=z;Если z=0,то
; Опр. Корнем n-ой степени из числа z наз.число w такое, что wn=z;Если z=0,то 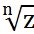 =0;если z
=0;если z 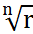 ; w=
; w=  +i
+i 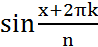 ) – корень n-ой степени.
) – корень n-ой степени.  (
(


