Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Плоские фигуры n-порядка заданные общим уравнением.Содержание книги
Поиск на нашем сайте Опр. Уравнение вида Определение. Фигуры плоскости, которые могут быть заданы уравнением вида (2.1) называют плоскими фигурами второго порядка.
Пусть Пусть в (2.1) Подставим новые значения
Где Условие (коэффициент
59◦.Эллиспоид Опр. Эллисоид назыв.фигура которая в некоторой специально выбранной прямоугольной системе координат может быть заданна ур-ние Если а=b=c,то уравнение x 2 +y 2 +z 2 =a 2 определяет сферу радиуса а. В силу того, что x,y,z входят в ур-ние в четной степени, то эллипсоид симметричен относительно начало координат, координатных плоскостей и координатных осей. Начало координат назыв. Центром эллипсоидом О(0,0,0) оси Ox,Oy,Oz назыв. Главной осью. Точки пересечения с главными осями наз. Вершинами эллипсоидом. А 1 (-a,0,0); A 2 (a,0,0); B 1 (0,-b,0); B 2 (0,b,0); C 1 (0,0,-c); C 2 (0,0,c). |x|≤a, |y|≤b, |z|≤c. В связи с этим все точки эллипсоида находятся внутри параллепипеда. x=a, x=-a; y=b, y=-b; z=c, z=-c; Если b=c, то ур-ние
Исследование формы эллипсоида методом сечений. Пусть Пусть каноническое ур-ние эллипсоида, исследуем данную фигуру сечением. Сечение плоскостью Oxy:z=0 Данная фигура эллипс, фокусы находятся на оси Ox. π||Oxy, π: z=h 1-h 2 /c 2 >0 сечение плоскостью Oyz x=0, π||Oyz, π:x=h, x=z,y=0; π||Oxy, y=h
61°. Однополостный и двуполостный гиперболоиды. Опр. Однополостный гиперболоид наз. Фигура, которая специально выбранной системе координат заданным ур-нием Опр. Двуполостный гиперболоид наз. Фигура которая в специально выбранной системе координат задается ур-нием Гиперболоиды симметричны относительно начало координат, координатных плоскостей, осей координат. Центр гипербола оси Ox,Oy,Oz –главные оси. Точки пересечения гиперболоида с главными осями наз. Вершина
Исследование формы гиперболоидов методом сечений. Пусть Oxy Oxz a) если |h|<b гиберболоида фокусы на оси Ox; b) если |h|>b фокусы будут лежать || оси Оz. c) |h|=b, y=b 1) Oxy
Б) |h|=c, В) |h|>c, 3) Oxz, гипербола фокусы кот. Находятся на оси Oz.
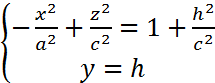
63°. Конус второго порядка. Опр. Конусом 2 порядка наз. Поверхность кот. Специально выбранной прямоугольной системе координат задается ур-нением Конус симметричен относительно Ox,Oy,Oz,O(0,0). Начало координат называется центром. Начало координат принадлежат конусу наз. Вершина конуса.
64. Исследование формы конуса второго порядка методом сечений. 1) Oxy 2) π||Oxy, 3) Oxz 4) π||Oxz,
65°. Эллиптический и гиперболический параболоиды. Опр. Эллиптическим параболоидом наз. Поверхность кот. В специально выбранной произвольной системе координат может быть заданна ур-нием Опр. Гиперболическим параюолоидом наз. Поврехность кот. В специально выбранной системе координат заданна ур-нием Начало координат принадлежит парабалоидам О(0,0,0) и это точка наз. Вершина парабалоида. Параболоиды симмитричны относительно плоскости Oxz,Oyz.
66. Исследование формы параболоидов методом сечений. 1) Oxy A) h<0, то пересечений нет Б) h>0, 3) Oxz 5) Oyz Гиперболический параболоид Oxy 3)Oxz
 ,парабалоида ветви направлены в противоположную сторону. ,парабалоида ветви направлены в противоположную сторону.
Цилиндры второго порядка. Эллиптический, гиперболический и параболический цилиндры. Опр. Пусть π-некоторая плоскость, ϒ-некоторая линия этой плоскости через каждую точку линии ϒ проведем прямые перпендикулярно плоскости π. Образовавшейся поверхность наз. Цилиндрической. Опр. Линия ϒ-явл. Фигурой 2 порядка, то цилиндрическая поверхность наз.цилиндром второго порядка.
|
||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 623; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |

 (2.1) где
(2.1) где  , называется уравнением второго порядка от двух переменных
, называется уравнением второго порядка от двух переменных  и
и  .
.
 – старая система координат,
– старая система координат,  – новая система координат.
– новая система координат. , тогда
, тогда  .
. и
и 
 Откуда имеем,
Откуда имеем,  ,
,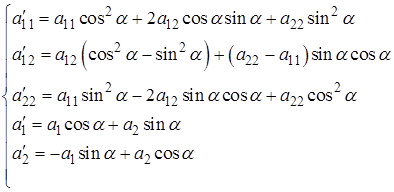
 имеет вид
имеет вид  (2.2). При повороте системы координат на угол
(2.2). При повороте системы координат на угол  из (2.2) уравнение (2.1) примет вид
из (2.2) уравнение (2.1) примет вид 
 ).
).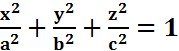 , где (a,b,c>0,ϵR).
, где (a,b,c>0,ϵR). (эллипсоид вращения, кот. получается вращением факальной плоскости)
(эллипсоид вращения, кот. получается вращением факальной плоскости)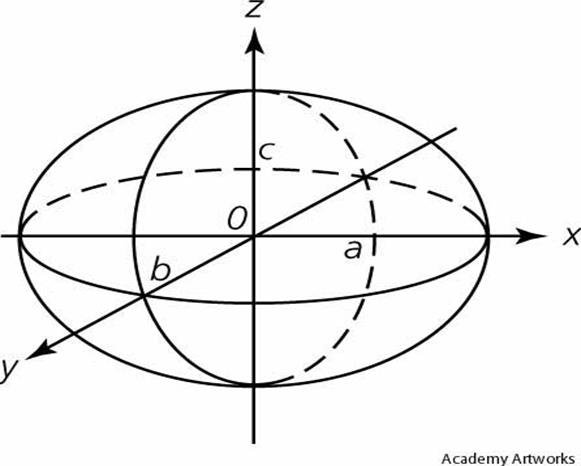
 , где a>b>c>0.
, где a>b>c>0. ;
; 

 чем больше |h|,то a, b меньше z=c, h=c c 1 (0,0,-c) c 2 (0,0,c)
чем больше |h|,то a, b меньше z=c, h=c c 1 (0,0,-c) c 2 (0,0,c) на оси Oy там фокусы
на оси Oy там фокусы ,
, 
 .
.


 где a,b,cϵR.
где a,b,cϵR. где a,b,cϵR.
где a,b,cϵR.

 , a>b. ( Однополостный гиперболоид рис.1 )
, a>b. ( Однополостный гиперболоид рис.1 ) 2) π||Oxy
2) π||Oxy 
 4) π||Oxz
4) π||Oxz 

 ур-ние пересекающихся прямых.
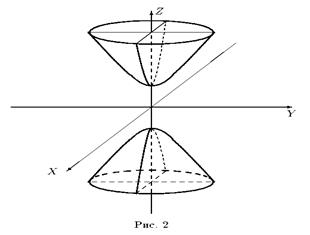
ур-ние пересекающихся прямых.  , где ( Двуполостный гиперболоид рис.2)
, где ( Двуполостный гиперболоид рис.2) 2) π||Oxy
2) π||Oxy 




 , a,b,c>0.
, a,b,c>0.


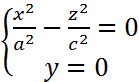


 , p,q>0
, p,q>0 , p,q>0.
, p,q>0.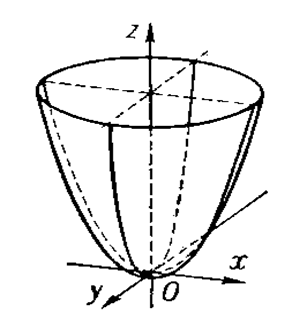

 2) π||Oxy
2) π||Oxy 

 4) π||Oxz
4) π||Oxz 

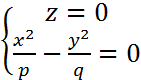 2) π||Oxy
2) π||Oxy