
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема (критерий квадрируемости).Содержание книги Поиск на нашем сайте
Плоская фигура D квадрируема тогда и только тогда, когда для любого сколь угодно малого Доказательство. Необходимость. Пусть фигура квадрируема, то есть По определению точной нижней грани для Тогда разность площадей описанного и вписанного многоугольников
Достаточность. Пусть нашлись многоугольники Так как
Теорема 1. Криволинейная трапеция, то есть фигура
Доказательство. Зафиксируем Тогда по критерию интегрируемости
Величина верхней суммы Дарбу Величина нижней суммы Дарбу Так как нашли многоугольники то по критерию квадрируемости криволинейная трапеция G является квадрируемой фигурой. Для оценки площади криволинейной трапеции справедливы неравенства
получаем формулу
Вычисление площадей плоских фигур Площадь плоской фигуры в декартовых координатах 1) Пусть плоская фигура представляет собой криволинейную трапецию
2) Пусть фигуру можно разбить на две криволинейные трапеции: под графиком
Пример. Вычислить площадь сектора с углом
Здесь первое слагаемое является площадью криволинейной трапеции под графиком линейной функции
Второе слагаемое представляет собой площадь под дугой окружности, задаваемой уравнением
Сделаем в интеграле замену переменной Пересчитаем пределы интегрирования: при
Складывая две вычисленные площади, находим площадь сектора
Пример. Найти площадь фигуры, ограниченной линиями Найдем сначала абсциссы точек пересечения графиков данных функций. Для этого решаем систему уравнений
Отсюда находим
Площадь фигуры, под графиком функции, заданной параметрически. Пусть плоская фигура представляет собой криволинейную трапецию, верхняя граница которой задана параметрическими уравнениями
В этом случае площадь вычисляется по формуле
Пример. Вычислить площадь эллипса. Зададим эллипс параметрическими уравнениями
Поскольку эллипс симметричен относительно координатных осей, то можно искать площадь четверти эллипса, расположенной в первой координатной четверти. Эта фигура представляет собой криволинейную трапецию, у которой абсцисса меняется от
Отсюда площадь всего эллипса равна
Площадь плоской фигуры в полярных координатах.
В полярных координатах через определенный интеграл находится площадь криволинейного сектора. Определение Криволинейный сектор – это фигура, ограниченная в полярных координатах лучами
Теорема. Если функция
Доказательство. Пусть
Тогда площадь криволинейного сектора разбилась на n частей. Обозначим через
Здесь в правой части интегральная сумма Римана для функции Поскольку функция
Перейдем к полярным координатам Найдем область определения функции из условия Решая это неравенство, находим Функция имеет период Так как
Вычисление объёмов
Телом назовём часть пространства, ограниченную замкнутой несамопересекающейся поверхностью. Понятие объема пространственного тела вводится аналогично понятию площади плоской фигуры. Пусть
Определение. Тело
Критерий кубируемости. Тело F кубируемо тогда и только тогда, когда для любого Доказательство проводится аналогично доказательству критерия квадрируемости.
Пример. Пусть Доказательство. Зафиксируем Тогда, по критерию кубируемости, призма кубируема. По определению объема
|
||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 2167; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.70.138 (0.006 с.) |

 найдутся многоугольники
найдутся многоугольники  и
и  , такие, что
, такие, что  и
и  .
. . Зафиксируем
. Зафиксируем 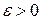 . По определению точной верхней грани для
. По определению точной верхней грани для  найдется вписанный многоугольник
найдется вписанный многоугольник  и
и  .
. и
и 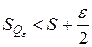 .
. .
. такие, что
такие, что  и
и 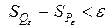 . Из определения точных верхней и нижней граней следует оценка
. Из определения точных верхней и нижней граней следует оценка  .
. - сколь угодно мало, то
- сколь угодно мало, то 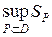 и
и  совпадают, следовательно, фигура квадрируема.
совпадают, следовательно, фигура квадрируема. , ограниченная линиями
, ограниченная линиями  ,
,  ,
,  ,
,  , где
, где  – непрерывна на отрезке
– непрерывна на отрезке  и
и  , является квадрируемой фигурой и ее площадь находится по формуле
, является квадрируемой фигурой и ее площадь находится по формуле  .
. .
. такое что
такое что  .
.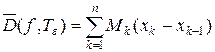 равна площади ступенчатой фигуры
равна площади ступенчатой фигуры  равна площади ступенчатой фигуры
равна площади ступенчатой фигуры  и
и  . Учитывая, что
. Учитывая, что  и
и  ,
, то есть фигуру, ограниченную линиями
то есть фигуру, ограниченную линиями  .
.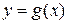 на отрезке
на отрезке  . Тогда ее площадь вычисляется по формуле
. Тогда ее площадь вычисляется по формуле .
. и радиусом
и радиусом 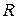 .
. Расположим сектор на координатной плоскости так, чтобы его вершина находилась с начале координат, и один из его радиусов лежал в положительной части оси
Расположим сектор на координатной плоскости так, чтобы его вершина находилась с начале координат, и один из его радиусов лежал в положительной части оси  . Тогда сектор можно разбить на две криволинейные трапеции, соответственно его площадь
. Тогда сектор можно разбить на две криволинейные трапеции, соответственно его площадь  .
. и вычисляется по формуле
и вычисляется по формуле .
. . Вычислим эту площадь:
. Вычислим эту площадь: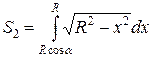 .
.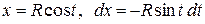 .
. ; при
; при . Подставляя
. Подставляя  в интеграл, получаем
в интеграл, получаем
 .
. 3) Пусть плоская фигура ограничена: сверху - графиком функции
3) Пусть плоская фигура ограничена: сверху - графиком функции  ; снизу - графиком функции
; снизу - графиком функции  .
. и
и  .
.
 . Искомая площадь вычисляется по формуле
. Искомая площадь вычисляется по формуле .
.
 .
.
 , что соответствует значению параметра
, что соответствует значению параметра  , до
, до  . Подставляя в формулу, находим
. Подставляя в формулу, находим .
. .
. и графиком функции
и графиком функции  .
.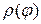 - непрерывна, то криволинейный сектор – квадрируемая фигура и площадь его находится по формуле
- непрерывна, то криволинейный сектор – квадрируемая фигура и площадь его находится по формуле .
. – разбиение отрезка
– разбиение отрезка 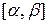 конечным набором точек
конечным набором точек
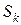 часть площади криволинейного сектора, ограниченного линиями
часть площади криволинейного сектора, ограниченного линиями  ,
,  достаточно мала, то
достаточно мала, то  и радиусом
и радиусом  , где
, где  произвольная точка из интервала
произвольная точка из интервала  . Тогда верно приближенное равенство
. Тогда верно приближенное равенство 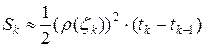 . А так как площадь криволинейного сектора равна
. А так как площадь криволинейного сектора равна  , то получаем приближенное равенство
, то получаем приближенное равенство .
. .
. интегральные суммы стремятся к интегралу Римана. Таким образом получаем формулу
интегральные суммы стремятся к интегралу Римана. Таким образом получаем формулу  .
. Пример. Найти площадь фигуры, ограниченной лемнискатой Бернулли, задаваемой уравнением
Пример. Найти площадь фигуры, ограниченной лемнискатой Бернулли, задаваемой уравнением  .
. . Тогда уравнение кривой примет вид
. Тогда уравнение кривой примет вид 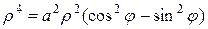 или
или  .
.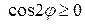 .
. .
. , значит ее график симметричен относительно начала координат.
, значит ее график симметричен относительно начала координат. , то график функции также симметричен относительно оси
, то график функции также симметричен относительно оси  . Тогда площадь фигуры, ограниченной лемнискатой
. Тогда площадь фигуры, ограниченной лемнискатой  .
. – некоторое тело в пространстве. Его нижний объем определяется по формуле
– некоторое тело в пространстве. Его нижний объем определяется по формуле  , где
, где  – множество всех многогранников, лежащих внутри
– множество всех многогранников, лежащих внутри  , где
, где  – множество всех многогранников, содержащих в себе
– множество всех многогранников, содержащих в себе  , тогда объем тела равен
, тогда объем тела равен  .
. и
и  такие что
такие что  и
и  .
.
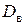 получено из нижнего основания
получено из нижнего основания  сдвигом на вектор
сдвигом на вектор  , перпендикулярный нижнему основанию (при этом, конечно, фигуры
, перпендикулярный нижнему основанию (при этом, конечно, фигуры  , где
, где  – высота призмы, то есть длина вектора
– высота призмы, то есть длина вектора  найдутся многоугольники
найдутся многоугольники  и
и  такие, что
такие, что 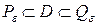 и
и  . Многогранник с высотой
. Многогранник с высотой  лежит внутри призмы, а многогранник с основанием
лежит внутри призмы, а многогранник с основанием 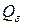 и высотой
и высотой  .
. . С другой стороны,
. С другой стороны,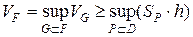 . Отсюда видно, что
. Отсюда видно, что 


