
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Извлечение корня из комплексного числа.Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Пусть комплексное число записано в тригонометрической форме Запишем его корень также в тригонометрической форме записи
По определению корня имеем Возводя в степень по формуле Муавра, получаем
Итак, корень степени n из комплексного числа извлекается по формуле
Для любого комплексного числа различных корней степени n ровно n штук. Все они расположены на окружности с центром в начале координат с радиусом Пример 2. Вычислить Запишем число i в тригонометрической форме Применим формулу извлечения корня из комплексного числа
Подставляя
Извлечение корня квадратного из комплексного числа в алгебраической форме записи.
Запишем квадратный корень из числа
Приравнивая действительные и мнимые части, а также, учитывая, что модуль числа
Решая эту систему, находим
Пример 3. Вычислить Действительная и комплексная части
Итак,
Многочлены. Разложение на множители.
Рассмотрим многочлен степени n с комплексными коэффициентами от комплексной переменной
Любой многочлен то есть представить в виде
Определение. Число z0 называется корнем многочлена
Теорема Безу. Число
Доказательство. Необходимость. Пусть с остатком: Положим в этом равенстве Достаточность. Пусть
Определение. Число
Утверждение. Число
Доказательство. Необходимость. Пусть известно, что Очевидно, что Ньютона-Лейбница
При Достаточность. Разложим многочлен
Так как первые k слагаемых в правой части обращаются в ноль, то многочлен можно представить в виде
При этом многочлен в точке Тогда
Основная теорема алгебры (без доказательства). Пусть
Лемма 1. Если z0 – корень кратности k многочлена
Доказательство. Если z0 – корень кратности k многочлена Возьмём сопряжённое к левой и правой частям последнего равенства
тогда Это и означает, что
Лемма 2. Пусть Если
Доказательство. По лемме 1 число Теорема. Многочлен от действительной переменной с действительными коэффициентами
Доказательство. Рассмотрим многочлен Тогда, по основной теореме алгебры, его можно представить в виде
Если Если кратности
можно представить в виде степени, в основании которой лежит квадратный трехчлен с отрицательным дискриминантом
Таким образом, разложили многочлен
|
||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 770; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.11.13 (0.007 с.) |

 .
.
 .
. . Отсюда находим модуль корня
. Отсюда находим модуль корня и аргумент
и аргумент ;
; 
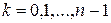 .
. где
где 
 и делят эту окружность на n равных частей.
и делят эту окружность на n равных частей. .
. .
. при
при  .
. получаем различные значения корня
получаем различные значения корня
 в алгебраической форме
в алгебраической форме . Возведем это равенство в квадрат:
. Возведем это равенство в квадрат:
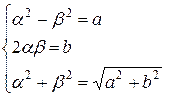
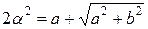 , откуда
, откуда .
. .
. равны a=3 и b=4. Вычислим по найденной формуле действительную и комплексную части его корня
равны a=3 и b=4. Вычислим по найденной формуле действительную и комплексную части его корня
 .
.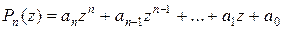 , где
, где  комплексная переменная;
комплексная переменная; комплексные числа.
комплексные числа. можно поделить на многочлен
можно поделить на многочлен  с остатком,
с остатком, где
где – делитель,
– делитель,  – остаток,
– остаток,  – частное.
– частное. =0.
=0. является корнем многочлена
является корнем многочлена  .
. , где R – число.
, где R – число. .
.  Так как
Так как  , следовательно
, следовательно  и
и  . Подставляя в это равенство
. Подставляя в это равенство 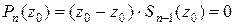 , следовательно, по определению,
, следовательно, по определению,  , если многочлен можно представить в виде
, если многочлен можно представить в виде  , где
, где  .
. включительно, то есть
включительно, то есть  а
а  .
. по формуле
по формуле
 все слагаемые в правой части в точке
все слагаемые в правой части в точке  . Если же
. Если же  , то в точке
, то в точке 

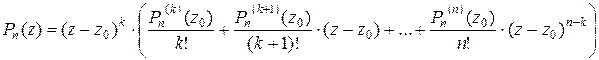 .
.
 по условию.
по условию. , где
, где – корень кратности
– корень кратности 
 является корнем кратности k для сопряженного многочлена
является корнем кратности k для сопряженного многочлена  .
. . По свойствам сопряжённых чисел имеем
. По свойствам сопряжённых чисел имеем . В левой части этого равенства стоит значение сопряженного многочлена в точке
. В левой части этого равенства стоит значение сопряженного многочлена в точке  и оно представимо в виде
и оно представимо в виде  где
где  Положив в этой формуле
Положив в этой формуле  , получим
, получим 
 . Обозначим
. Обозначим 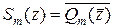 ,
, , где
, где 
 .
. – многочлен с действительными коэффициентами, но от комплексной переменной.
– многочлен с действительными коэффициентами, но от комплексной переменной. корень кратности k многочлена
корень кратности k многочлена 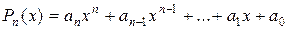 представляется в виде произведения линейных множителей и квадратных с отрицательным дискриминантом:
представляется в виде произведения линейных множителей и квадратных с отрицательным дискриминантом: , где
, где – действительный корень кратности
– действительный корень кратности  ;
; 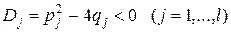 ;
;  .
. как многочлен от комплексной переменной
как многочлен от комплексной переменной  .
. не преобразовываем.
не преобразовываем. то
то  , где
, где  . По лемме 2, если
. По лемме 2, если  – корень
– корень для
для 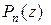 , то
, то  также корень кратности
также корень кратности  . Сопряженное число запишется как
. Сопряженное число запишется как  , тогда произведение
, тогда произведение
 так как
так как  .
. , получим искомое разложение для
, получим искомое разложение для 


