
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кратность корней. Нахождение кратности корня с помощью схемы ГорнераСодержание книги
Поиск на нашем сайте
Пусть разложение полинома
Среди
где Определение 10.2. Если Задача 2. Имеет ли данный полином кратный корень? Если да, то какова его кратность? Теорема 10.1. Пусть
где
Замечание 10.2. Итак, для того, чтобы ответить на вопрос «имеет ли данный полином кратный корень?», необходимо найти Если корень λ полинома Чтобы ответить на вопрос «какова кратность корня?», построим последовательность:
Упражнение 10.1.
Способ нахождения всех кратных корней Если уравнение
т. к.
Так продолжаем до тех пор, пока не найдется
Все корни полиномов Следовательно, найдя полиномы
получим полиномы
Замечание 10.3. Если поделить Замечание 10.4. Этот способ определения кратности корней, их существования, используется в случае, когда сложно разложить Пример 10.2.
Замечание 10.5. Таким образом, схема Горнера используется: 1) для вычисления 2) для вычисления полинома 3) для вычисления производных 4) для разложения 5) для определения кратности корня Д/з: П 541, 544 (b), 545 (d), 547, 548 (b), 549, 551, 588, 591, 631(b, c), 634 (b), 636 a), 638, 639 (a, b, c). Занятие 9. Решение уравнений 3-й и 4-й степени Решение уравнений 3-й степени Рассмотрим уравнение
(разделив, если надо, на
Пусть Обозначим
Положим
Пусть
Тогда из (9.2)
По теореме Виета неизвестные
Решая его, получим
Отсюда
Определение 9.1. Величина Формула Кардано
Так как в этой формуле
Тогда Вспоминая, что
получим
Соответствующие значения для
Так как
и
то, подставив полученное значение
Тогда
где Пример 9.1. П 75 о).
Таким образом,
Упражнение 9.1. П 75 j), n). Решение уравнений 4-й степени Общий вид уравнения 4-ой степени
Первые два члена можно преобразовать:
Сделаем замену
Введем вспомогательную переменную
Для того чтобы получить разность квадратов, достаточно воспользоваться введенной переменной
Пусть
при некоторых
Приравнивая к нулю каждый из сомножителей, найдем 4етыре корня исходного уравнения. Уравнение 9.2. П 75j), n); 79 i), j). Д/з: П 75 (а, b, c), 79 a), 80. Занятие 12. Полиномы над полем 12.1. Решение уравнений Теорема №1 Если f(x) имеет корень равный Упражнение №587(a) a) (x-1)2*(x-2)*(x-3)*(x-(1+i))*(x-(1-i)) = = (x2-2x+1)*(x2-5x+6)((x-1)+i)*((x-1)-I)= = (x4-2x2+x2-5x3+10x2-5x+6x2-12x+6)*((x-1)2-i2) = = (x4-7x3+17x2-17x+6)*(x2-2x+1+1) = = (x4-7x3+17x2-17x+6)*(x2-2x+2) = = x6-7x5+17x4-17x3+6x2-2x5+14x4-34x3+34x2-12x+2x4-14x3+34x2+12 = = x6-9x5+33x4-65x3+74x2-46x+12.
|
||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 2517; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.136.19.136 (0.009 с.) |

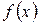 на линейные множители
на линейные множители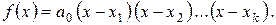
 могут быть совпадающие. Если они есть, то
могут быть совпадающие. Если они есть, то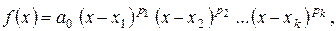 (10.1)
(10.1)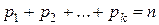 , а среди
, а среди 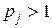 , то корень
, то корень  называется кратным корнем кратности
называется кратным корнем кратности 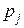 , если
, если 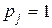 то корень
то корень 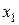 - кратный корень кратности
- кратный корень кратности 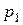 полинома
полинома  кратности
кратности  .
.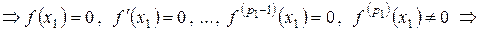


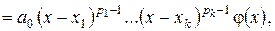
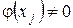 ,
, 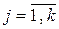 ,
, 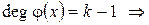
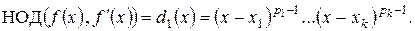
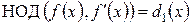 можно также найти по алгоритму Евклида.
можно также найти по алгоритму Евклида. , то «нет», иначе – «да».
, то «нет», иначе – «да».
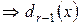 имеет только простые корни;
имеет только простые корни;  эти корни будут корнями кратности r полинома
эти корни будут корнями кратности r полинома 
 можно найти корни. Они будут кратными корнями
можно найти корни. Они будут кратными корнями 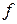 .
. достаточно большей степени и его решить не удается, то построим последовательность:
достаточно большей степени и его решить не удается, то построим последовательность: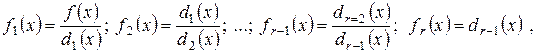

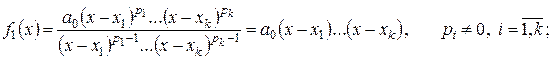
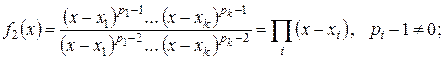
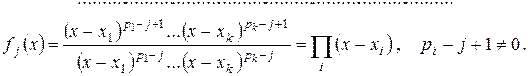
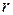 :
: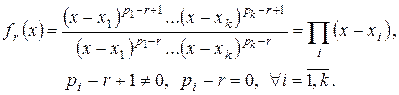
 – простые, однако, среди корней полинома
– простые, однако, среди корней полинома 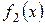 нет простых корней полинома
нет простых корней полинома 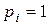 , а в полином
, а в полином 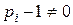 ); среди корней
); среди корней 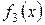 нет корней кратности 2 полинома
нет корней кратности 2 полинома 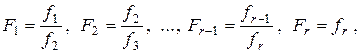
 , корни которых простые и являются корнями кратности j полинома
, корни которых простые и являются корнями кратности j полинома 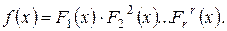
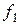 на
на 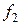 , то уйдут те простые корни
, то уйдут те простые корни 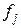 ,
, 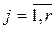 , не содержатся, следовательно, кратность этих корней в полиноме
, не содержатся, следовательно, кратность этих корней в полиноме 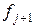 , то останутся корни кратности j в полиноме
, то останутся корни кратности j в полиноме 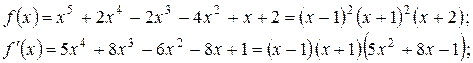
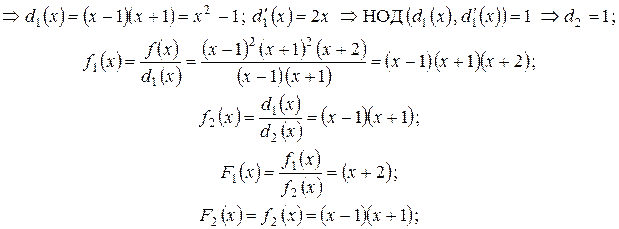

 - кратность 2,
- кратность 2, 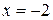 - кратность 1.
- кратность 1.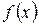 при
при 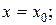
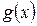 при делении
при делении 

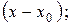
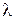 полинома
полинома 
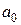 ). Заменим
). Заменим 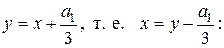
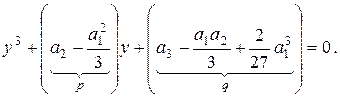
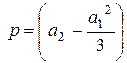 и
и 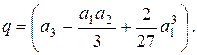
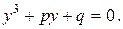 (9.1)
(9.1) , где
, где 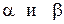 пока неизвестные величины
пока неизвестные величины (9.2)
(9.2)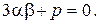 (9.3)
(9.3)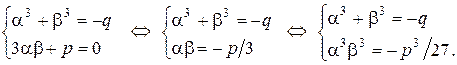
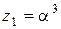 и
и 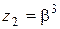 удовлетворяют квадратному уравнению:
удовлетворяют квадратному уравнению: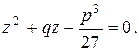
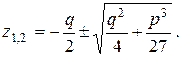
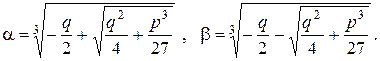 (9.4)
(9.4)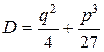 называется дискриминантом кубического полинома (9.1)
называется дискриминантом кубического полинома (9.1)
 может принимать три значения и
может принимать три значения и 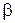 тоже три значения, то всевозможных комбинаций
тоже три значения, то всевозможных комбинаций  может быть девять, а
может быть девять, а  может быть всего три, в силу дополнительной связи (9.3). Если определим
может быть всего три, в силу дополнительной связи (9.3). Если определим 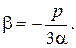
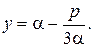
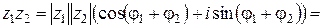
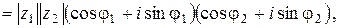 (9.5)
(9.5)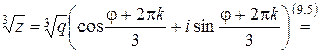
 (9.6)
(9.6) т. е. равно произведению какого-то корня на всё множество кубических корней из 1:
т. е. равно произведению какого-то корня на всё множество кубических корней из 1: 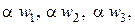 где
где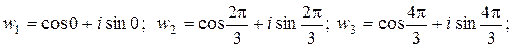

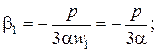
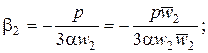
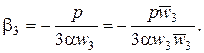
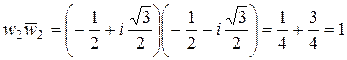

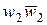 и
и 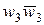 в соответствующие значения для
в соответствующие значения для 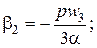
 .
.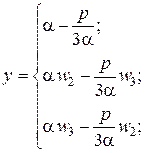
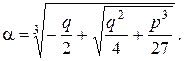
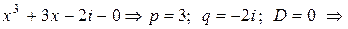
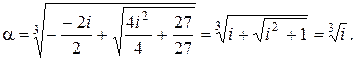
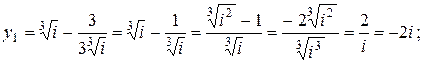
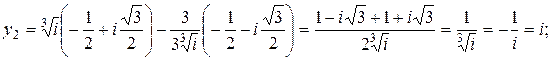



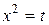 ,тогда
,тогда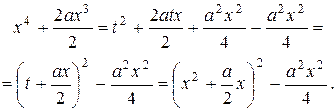
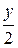 :
: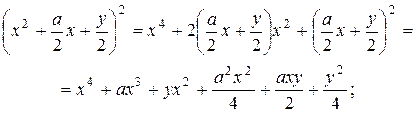
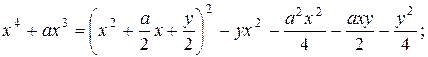

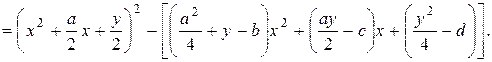
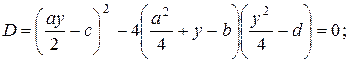
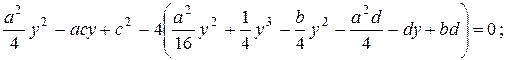




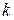 и
и 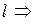
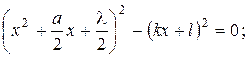
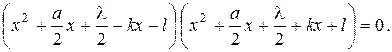
 . Приводимость. Полиномы над полем
. Приводимость. Полиномы над полем 
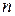 -й степени
-й степени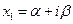 , такой, что
, такой, что  , то f(x) имеет сопряжённый корень
, то f(x) имеет сопряжённый корень  .
.


