
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Занятие 8. Полиномы. Действия над полиномами. Схема ГорнераСодержание книги
Поиск на нашем сайте Занятие 8. Полиномы. Действия над полиномами. Схема Горнера Полиномы. Определение Определение 8.1. Многочленом (полиномом) называется функция
Определение 8.2. Говорят, что полином Определение 8.3. Два полинома Теорема 8.1. Два полинома
Действия над полиномами Для полинома определяются операции сложения и умножения:
Упражнение 8.1. Найти многочлены Схема Горнера. Вычисление значения полинома в точке Задача 1. Как вычислить значение При вычислении «в лоб», т. е.
И начинаем вычислять с самой внутренней скобки. Получаем 2 n операций. Именно этот алгоритм реализован в схеме Горнера.
где Легко видеть, что Пример 8.1.
Упражнение 8.2. 544а). 8.4. Схема Горнера. Вычисление корней полинома и нахождение полинома степени Основная задача классической высшей алгебры – решение уравнений и систем уравнений. Рассмотрим уравнение
где Определение 8.4. Уравнение (8.1) называется алгебраическим. Определение 8.5. Значение Упражнение 8.3. П 75p), Существует ли у уравнения (8.1) хотя бы один корень? Теорема 8.2. (Основная теорема высшей алгебры). Уравнение (8.1) имеет, по крайней мере, один корень Определение 8.6. Выражение вида Теорема 8.3. (Безу). Полином
где Доказательство. Пусть
Как видим выражения для
Пример 8.2.
Упражнение 8.4. Найти Итак, если найден один корень уравнения (8.1), то можно понизить степень на 1 и рассматривать уравнение
Теорема 8.4. (Следствие к основной теореме высшей алгебры). Каждый полином
И такое представление единственно. Определение 8.7. Представление (8.2) называется разложением полинома на линейные множители. Пример 8.3. В П 75p) разложить
(как видим в таком представлении могут встречаться и одинаковые линейные множители) Упражнение 8.5. П 582 d). Теорема 8.5. (Виета). Пусть корни многочлена
равны
Пример 8.4.
Д/з: 544 b), 582, 618, 624 (а, b), 626. Занятие 9. Деление полиномов. НОД. Алгоритм Евклида. Линейное представление НОД Деление полиномов. НОД Теорема 9.1. (О делении с остатком). Для полиномов
где Упражнение 9.1. П 539 а). Имеется полная аналогия между множеством целых чисел и множеством полиномов. Определение 9.1. Пусть Определение 9.2. НОД – полином наибольшей степени из бесконечного множества общих делителей. Алгоритм Евклида Как найти НОД? I. Разложить оба многочлена на линейные множители. Упражнение 9.2. П 588 а). II. Алгоритм Евклида. Пусть
Упражнение 9.3. П 631 а). Линейное представление НОД Теорема 9.2. Пусть
Замечание 9.1. Найти Упражнение 9.4. П 632 а). Теорема 9.3. Полиномы
При этом будет выполняться
Упражнение 9.5. П 634 а). Д/з: П 588, 641 d), c), 551, 541, 634 b), 636 a), 638. Занятие 10. разложение полинома по степеням 10.1. Формула ТеЙлора, разложение полинома по степеням Любую
где Определение 10.1. Назовем такое представление разложением Задача 1. Пусть имеется полином
Требуется разложить
Эту задачу можно решать двумя способами: 1) Так как 2) можно воспользоваться схемой Горнера
Пример 10.1.
1)
2)
Замечание 10.2. Очевидно, что с помощью схемы Горнера возможно вычисление значений производных в точках. Упражнение 10.1.
Пример 10.2.
Замечание 10.5. Таким образом, схема Горнера используется: 1) для вычисления 2) для вычисления полинома 3) для вычисления производных 4) для разложения 5) для определения кратности корня Д/з: П 541, 544 (b), 545 (d), 547, 548 (b), 549, 551, 588, 591, 631(b, c), 634 (b), 636 a), 638, 639 (a, b, c). Границы корней полиномов. Теорема №2 Пусть f(x)=
где А – max из mod отрицательных коэффициентов.
Теорема №3(Ньютона) Число а есть верхняя граница положительных корней полинома f(x), если f(a)>0, f’(a)>0,…, Замечание №1 Чтобы получать оценку снизу, следует … (-1)n f(-x) и оценить его корни сверху. Замечание №2 Если все коэффициенты f(x) Упражнение №693
Пусть Теорема №4. Если f(x) имеет корень Упражнение №664(а)
Следовательно И тогда мы делим Прировняем его к нулю и решим как квадратное уравнение:
Пусть Теорема №5 Если f(x) имеет корень 1) 2) p делитель 3) p-mq делитель f(m), т.е. Замечание №3 В частности, Упражнение 664(а)
D=4+48=52=4*13;
Замечание №4 Если в f(x) Замечание №5 Уравнение с целочисленными коэффициентами чаще всего не имеет рациональных корней. Возвратные полиномы. Определение №2
Пример.
Обозначим Утверждение №1 f возвратен тогда и только тогда, когда Но Теорема №6 Если n- нечётная, то возвратный полином имеет корень Доказательство: Вычислим Упражнение №582.
Поделим его на х2:
Пусть D =24;
Следовательно
D =
Упражнение №1
Поделим на х3:
Теорема №7 Признак неприводимости Эйзенштейна. Пусть p – просто число.
Занятие 8. Полиномы. Действия над полиномами. Схема Горнера Полиномы. Определение Определение 8.1. Многочленом (полиномом) называется функция
Определение 8.2. Говорят, что полином Определение 8.3. Два полинома Теорема 8.1. Два полинома
Действия над полиномами Для полинома определяются операции сложения и умножения:
Упражнение 8.1. Найти многочлены
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 1833; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.113 (0.01 с.) |


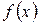 имеет степень n, если
имеет степень n, если  . Обозначение:
. Обозначение:  .
. называются тождественно равными, если
называются тождественно равными, если  при всех
при всех  где
где  и
и  .
. тождественно равны
тождественно равны  тогда и только тогда, когда выполнены два условия:
тогда и только тогда, когда выполнены два условия:


 .
. наискорейшим образом?
наискорейшим образом? , потребуется
, потребуется  раз возводить в степень, потом n раз умножать на
раз возводить в степень, потом n раз умножать на 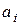 и n раз складывать:
и n раз складывать:  действий. Попробуем считать по-другому:
действий. Попробуем считать по-другому:


 .
.


 (8.1)
(8.1)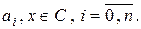
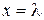 называется корнем полинома
называется корнем полинома  .
. .
.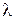 , в общем случае комплексный.
, в общем случае комплексный. называется линейным множителем для многочлена
называется линейным множителем для многочлена 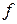 .
.
 .
. и
и  . Тогда
. Тогда



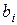 совпадают с выражениями в первой строке схемы Горнера
совпадают с выражениями в первой строке схемы Горнера



 для П 75p),
для П 75p),  ,
,  .
.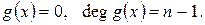
 (8.2)
(8.2)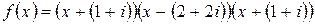

 , тогда
, тогда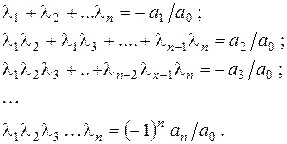

 существуют и единственны полиномы
существуют и единственны полиномы  и
и  , такие что:
, такие что:
 .
. . Тогда
. Тогда  называется общим делителем
называется общим делителем  .
. . Разделим
. Разделим  на
на  с остатком:
с остатком: ;
; 
 ;
; 
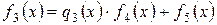 ;
; 
 , где
, где 

 или последний, не равный нулю остаток.
или последний, не равный нулю остаток. . Тогда существуют полиномы
. Тогда существуют полиномы  такие, что
такие, что
 и
и  можно с помощью алгоритма Евклида аналогично тому, как искали линейное представление НОД для целых чисел.
можно с помощью алгоритма Евклида аналогично тому, как искали линейное представление НОД для целых чисел. взаимно просты (
взаимно просты ( ) тогда и только тогда, когда существуют два полинома
) тогда и только тогда, когда существуют два полинома  такие, что
такие, что

 через схему Горнера. Кратные корни. Отыскание кратности корня с помощью схемы Горнера
через схему Горнера. Кратные корни. Отыскание кратности корня с помощью схемы Горнера (через схему Горнера)
(через схему Горнера)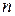 раз дифференцируемую в точке
раз дифференцируемую в точке  функцию можно разложить в ряд Тейлора:
функцию можно разложить в ряд Тейлора:
 , если
, если  .
.
 , т. е. найти неизвестные коэффициенты в разложении
, т. е. найти неизвестные коэффициенты в разложении
 , то, раскрывая скобки по биному и подставив в
, то, раскрывая скобки по биному и подставив в 
 В остальных строках вычисляются
В остальных строках вычисляются





 можно найти корни. Они будут кратными корнями
можно найти корни. Они будут кратными корнями 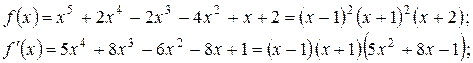
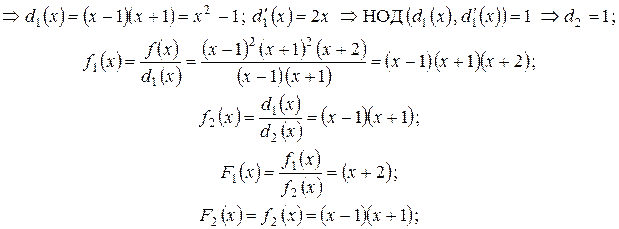

 - кратность 2,
- кратность 2, 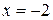 - кратность 1.
- кратность 1.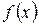 при
при 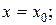
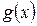 при делении
при делении 

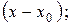
 ,
,  . Верхняя граница положительных корней полинома f(x)
. Верхняя граница положительных корней полинома f(x)  может быть принята равной одному из чисел.
может быть принята равной одному из чисел. (Макларен)
(Макларен) (Лагранж),
(Лагранж), - индекс первого отрицательного коэффициентов.
- индекс первого отрицательного коэффициентов.
 0, то f(x) не имеет положительных корней.
0, то f(x) не имеет положительных корней.


 ,
,  ,
, 
 , то
, то 

 , т.е.
, т.е.  .
. .
.

 .
. ,
,  и при этом
и при этом  является несократимой дробью, то:
является несократимой дробью, то: делитель
делитель  , т.е.
, т.е. 
 , т.е.
, т.е. 


 ;
;  .
.


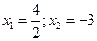

 /
/ , то f(x) можно свести f(x) c
, то f(x) можно свести f(x) c  ,
,  , …,
, …,  , …, по (сравнивать) коэффициенты
, …, по (сравнивать) коэффициенты  симметрично относительно середины.
симметрично относительно середины. - бином.
- бином.
 .
. , следовательно возвратные полиномы удовлетворяют функциональному соотношению
, следовательно возвратные полиномы удовлетворяют функциональному соотношению  .
. .
.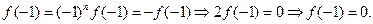 Следовательно f(x) нечётной степени можно представить в виде f(x)=(x+1)g(x), где g(x) – возвратный полином чётной степени.
Следовательно f(x) нечётной степени можно представить в виде f(x)=(x+1)g(x), где g(x) – возвратный полином чётной степени. ;
; ;
;















 ;
; f не приводим над полем
f не приводим над полем  .
.


