
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава. Интегральное исчисление функций одного переменногоСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Глава. Интегральное исчисление функций одного переменного
Определение и свойства неопределённого интеграла
Первообразная и неопределенный интеграл
К числу важных задач механики относятся задача о нахождении закона движения материальной точки по ее заданной скорости, а также задача об нахождении закона движения и скорости материальной точки по ее заданному ускорению. Эти задачи приводят к математической проблеме отыскания функции по заданной производной этой функции.
Определение. Функция 1) 2)
Пример. Для функции
Следующее утверждение сразу следует из определения первообразной: Лемма 1. Если
Верно и обратное утверждение: Лемма 2. Пусть то есть Доказательство. Найдем производную от разности этих первообразных:
Следствие. Если Определение. Неопределённый интеграл функции
Из этого определения и предыдущего следствия видим, что
Свойства неопределённого интеграла 1) 2) 3) 4)
Доказательство. 1).
2).
3). Пусть
Так как
4). Пусть
Так как
Первые два свойства неопределённого интеграла говорят о том, что дифференцирование и интегрирование – взаимно обратные операции. Третье и четвертое свойства означают, что операция интегрирования линейна. Свойства 1), 3) и 4) используются для вычисления интегралов.
Таблица основных неопределенных интегралов 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13) 14) 15) 16) 17) 18)
Некоторые, наиболее простые интегралы можно вычислять, пользуясь только таблицей и свойствами. Пример 1. Вычислить интеграл В числителе дроби прибавим и вычтем 1, затем, поделив почленно, получим разность двух табличных интегралов:
Пример 2. Вычислить интеграл Применим тригонометрическую формулу понижения степени:
Пример 3. Вычислить интеграл Числитель подынтегральной дроби, в силу основного тригонометрического тождества, представим в виде:
Однако, в большинстве случаев для вычисления интегралов необходимы дополнительные методы. Основные из них – это метод замены переменной и метод интегрирования по частям. Некоторые сведения о комплексных числах и многочленах
Интегрирование рациональных функций.
Рациональная функция – это отношение двух многочленов Интегрирование иррациональных функций
Интеграл от иррациональной функции сводится к вычислению интеграла от рациональной функции путём замены переменной. Рассмотрим многочлен от двух переменных степени не превосходящей натурального числа
Рассмотрим наиболее часто встречающиеся типы иррациональностей. Подстановки Эйлера.
Подстановки Эйлера используются для вычисления интеграла вида
Он рационализируется в трёх случаях.
1 случай: a > 0. В этом случае делаем замену
Затем находим значение корня и дифференциала через новую переменную
Подставляя все в исходный интеграл, получаем интеграл от рациональной функции
2 случай: c > 0. В этом случае делаем замену Возводим обе части последнего равенства в квадрат и выражаем старую переменную через новую переменную:
Затем находим значение корня и дифференциала через новую переменную
Подставляя все в исходный интеграл, получаем интеграл от рациональной функции.
3 случай: Уравнение
В этом случае делаем замену Возводим обе части последнего равенства в квадрат и выражаем старую переменную через новую переменную:
Затем выражаем через новую переменную значение корня и дифференциала
Подставляем эти выражения в исходный интеграл и вычисляем интеграл от рациональной функции.
Пример 4. Вывести формулу для вычисления табличного интеграла Коэффициент при Сделаем замену
Затем выражаем через новую переменную значение корня и дифференциала
Подставив эти выражения под интеграл, получим табличный интеграл
Пример 5. Вычислить интеграл В данном примере подходит и первый и второй случаи. Применим вторую подстановку Эйлера, сделаем замену Возведем в квадрат
Подынтегральная дробь является правильной, её нужно представить в виде суммы простейших дробей Определенный интеграл
Определение. Если существует конечный предел интегральных сумм при
Задача о массе стержня.
Рассмотрим сначала однородный стержень длины L, имеющий постоянную линейную плотность P. Тогда масса стержня находится по формуле
Пусть теперь стержень неоднородный, имеющий длину L и переменную линейную плотность. Выведем формулу для массы такого стержня. Расположим стержень на оси
Если длину наибольшего из частичных отрезков разбиения
Свойства сумм Дарбу 1) Для одной и той же функции и конкретного разбиения верхняя сумма Дарбу всегда не меньше, чем нижняя:
2) При измельчении разбиения, то есть при добавлении новых точек к исходному разбиению, верхние суммы Дарбу для одной и той функции не увеличиваются, а нижние суммы Дарбу не уменьшаются.
3) Для одной и той же функции и любых разбиений
Доказательства этих свойств можно найти в литературе.
Зафиксируем некоторое разбиение
Аналогично существует конечная точная верхняя грань у множества всех нижних сумм Дарбу и эта величина называется нижним интегралом Римана от функции
Определение. Если верхний интеграл равен нижнему, то функция
Длина дуги Понятие длины дуги Пусть кривая
Разобьем отрезок
соответствует точка Обозначим через Вычисление длины дуги Рассмотрим общий случай, когда кривая задана параметрическими уравнениями
Обозначим через Известна формула для дифференциала длины дуги
Циклоида – это траектория фиксированной точки, находящейся на ободе колеса, катящегося без проскальзывания. Параметрические уравнения циклоиды
Одна арка задается изменением параметра Упростим подынтегральное выражение в формуле для вычисления длины дуги
Подставляя в формулу и вычисляя интеграл, получаем:
Площадь плоской фигуры
Определение Криволинейный сектор – это фигура, ограниченная в полярных координатах лучами
Теорема. Если функция
Доказательство. Пусть
Тогда площадь криволинейного сектора разбилась на n частей. Обозначим через
Здесь в правой части интегральная сумма Римана для функции Поскольку функция
Перейдем к полярным координатам Найдем область определения функции из условия Решая это неравенство, находим Функция имеет период Так как
Вычисление объёмов
Телом назовём часть пространства, ограниченную замкнутой несамопересекающейся поверхностью. Понятие объема пространственного тела вводится аналогично понятию площади плоской фигуры. Пусть
Определение. Тело
Критерий кубируемости. Тело F кубируемо тогда и только тогда, когда для любого Доказательство проводится аналогично доказательству критерия квадрируемости.
Пример. Пусть Доказательство. Зафиксируем
Тогда, по критерию кубируемости, призма кубируема. По определению объема
Объём тела вращения
Пример. Найти объём конуса радиуса Конус – это тело, которое можно получить вращением вокруг оси
В случае вычисления объема тела, полученного вращением вокруг оси Пример. Найти объём тела, полученного вращением астроиды вокруг оси
Параметрические уравнения астроиды
Так как кривая симметрична относительно обеих координатных осей, то можно считать только половину объема тела – это объем тела, полученного вращением части кривой, соответствующей изменению параметра от Сделаем в этом интеграле замену Пересчитаем пределы интегрирования: при
Удваивая полученный результат, получаем окончательный ответ
Теоремы Паппа-Гульдина
Впервые эти теоремы нашел александрийский математик Папп в 3 веке н.э. В эпоху средневековья многие достижения античной науки были в Европе утрачены. В 17-ом веке теоремы вновь открыл швейцарский математик Гульдин.
Первая теорема Паппа-Гульдина. Площадь поверхности, образованной вращением кривой вокруг не пересекающей её оси, равна произведению длины кривой на путь, проходимый центром тяжести этой кривой. В случае вращения вокруг оси
Доказательство. Рассмотрим случай плоской кривой, когда она задана явно уравнением
Затем домножим обе части этого равенства на
В правой части этого равенства стоит площадь поверхности тела, образованного вращением кривой вокруг оси В левой части равенства стоит произведение длины кривой Пример 1. Найти координаты центра тяжести полуокружности радиуса
Пример 2. Найти площадь поверхности вращения полуокружности вокруг касательной, параллельной её диаметру.
Тогда радиус окружности, описываемой центром тяжести при вращении полуокружности вокруг касательной, равен
Вторая теорема Паппа-Гульдина. Объём тела, образованного вращением плоской фигуры вокруг не пересекающей её оси, равен произведению площади фигуры на путь, проходимый центром тяжести этой фигуры. В случае вращения вокруг оси
Доказательство. Рассмотрим случай плоской кривой, когда она задана явно уравнением
В правой части стоит объем тела, полученного вращением кривой вокруг оси Теорема доказана.
Пример 3. Найти координаты центра тяжести полукруга радиуса R с центром в начале координат, расположенного в верхней полуплоскости.
|
|||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 572; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.180.158 (0.016 с.) |

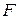 называется первообразной для функции
называется первообразной для функции  на промежутке X, если в каждой точке
на промежутке X, если в каждой точке  из промежутка X:
из промежутка X: , то в ней должна существовать соответствующая односторонняя производная);
, то в ней должна существовать соответствующая односторонняя производная); .
. первообразной является, например, функция
первообразной является, например, функция  . Очевидно, что функция
. Очевидно, что функция  -также ее первообразная.
-также ее первообразная. – некоторая первообразная для функции
– некоторая первообразная для функции  , то
, то  также является первообразной для функции
также является первообразной для функции  и
и  – две первообразные для функции
– две первообразные для функции  .
. . Тогда, по теореме об условиях постоянства функции на промежутке,
. Тогда, по теореме об условиях постоянства функции на промежутке,  .
. , где
, где  .
. .
. .
.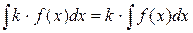 при
при  .
. .
. .
. .
. является первообразной для функции
является первообразной для функции  . Тогда
. Тогда , (1)
, (1) . (2)
. (2) и
и  – произвольные константы, то
– произвольные константы, то  – тоже произвольная константа. Поэтому правые, а, значит, и левые части в равенствах (1) и (2) равны.
– тоже произвольная константа. Поэтому правые, а, значит, и левые части в равенствах (1) и (2) равны. – первообразная для
– первообразная для  . Тогда
. Тогда  – первообразная для
– первообразная для  . Поэтому выполняются равенства
. Поэтому выполняются равенства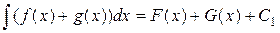 (3)
(3) . (4)
. (4) ,
,  – произвольные константы, то в равенствах (3) и (4) правые, а, значит, и левые части равны. ■
– произвольные константы, то в равенствах (3) и (4) правые, а, значит, и левые части равны. ■ .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
.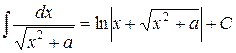 .
. .
. .
. .
. .
.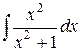 .
. ;
; .
. . Затем вынесем постоянный множитель
. Затем вынесем постоянный множитель  за знак интеграла и получим сумму двух табличных интегралов:
за знак интеграла и получим сумму двух табличных интегралов: .
. .
. . Затем поделим дробь почленно и получим сумму двух табличных интегралов:
. Затем поделим дробь почленно и получим сумму двух табличных интегралов: .
. .
. :
: . Отношение двух таких многочленов
. Отношение двух таких многочленов – это рациональная функция от двух переменных.
– это рациональная функция от двух переменных.
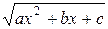 =
=  , где перед слагаемыми
, где перед слагаемыми  и
и  могут стоять произвольные знаки плюс или минус. Возводим обе части последнего равенства в квадрат и выражаем старую переменную через новую переменную:
могут стоять произвольные знаки плюс или минус. Возводим обе части последнего равенства в квадрат и выражаем старую переменную через новую переменную:

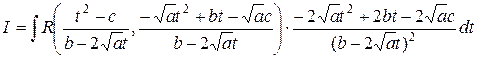 .
. .
.

 .
. имеет два различных действительных корня
имеет два различных действительных корня и
и  .
. .
.


 .
. положительный, значит подходит первый случай.
положительный, значит подходит первый случай. . Возведем в квадрат и выразим старую переменную через новую переменную
. Возведем в квадрат и выразим старую переменную через новую переменную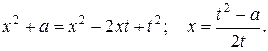


 .
. .
. , затем поделим на
, затем поделим на  . Отсюда выражаем старую переменную, затем корень и дифференциал через новую переменную.
. Отсюда выражаем старую переменную, затем корень и дифференциал через новую переменную.

 Подставим полученные выражения в исходный интеграл, получим интеграл от рациональной функции
Подставим полученные выражения в исходный интеграл, получим интеграл от рациональной функции
 , затем проинтегрировать эти дроби.
, затем проинтегрировать эти дроби. , и этот предел на зависит ни от выбора разбиения, ни от выбора точек
, и этот предел на зависит ни от выбора разбиения, ни от выбора точек  внутри каждого частичного отрезка разбиения, то такой предел называется определённым интегралом Римана от функции
внутри каждого частичного отрезка разбиения, то такой предел называется определённым интегралом Римана от функции 

 .
. – класс функций, интегрируемых по Риману на отрезке
– класс функций, интегрируемых по Риману на отрезке  .
. . Начало стержня обозначим точкой
. Начало стержня обозначим точкой  , конец стержня в точке
, конец стержня в точке  . Плотность стержня в точке
. Плотность стержня в точке  обозначим
обозначим  . Рассмотрим случай, когда функция
. Рассмотрим случай, когда функция  . Обозначим через
. Обозначим через  массу стержня, соответствующую частичному отрезку разбиения
массу стержня, соответствующую частичному отрезку разбиения . Тогда масса стрежня равна сумме масс всех таких его частей
. Тогда масса стрежня равна сумме масс всех таких его частей  . Если части достаточно маленькие, то функция
. Если части достаточно маленькие, то функция  . Будем считать плотность стержня на отрезке
. Будем считать плотность стержня на отрезке  постоянной и равной
постоянной и равной  . Тогда верно приближенное равенство
. Тогда верно приближенное равенство . Масса всего стержня тогда приблизительно равна
. Масса всего стержня тогда приблизительно равна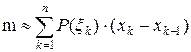 .
. устремить к нулю, то приближенное равенство для массы становится точным и верна формула
устремить к нулю, то приближенное равенство для массы становится точным и верна формула .
. .
. и
и  верхняя сумма Дарбу, соответствующая разбиению
верхняя сумма Дарбу, соответствующая разбиению  .
. . Рассмотрим семейство всех верхних сумм Дарбу
. Рассмотрим семейство всех верхних сумм Дарбу  . В силу свойства 3) сумм Дарбу,
. В силу свойства 3) сумм Дарбу, , то есть множество всех верхних сумм Дарбу ограничено снизу, поэтому существует конечная точная нижняя грань у этого множества и эта величина называется верхним интегралом Римана от функции
, то есть множество всех верхних сумм Дарбу ограничено снизу, поэтому существует конечная точная нижняя грань у этого множества и эта величина называется верхним интегралом Римана от функции  .
. .
. следует, что
следует, что  и выполняется равенство
и выполняется равенство .
. задана уравнениями
задана уравнениями .
. . Значению параметра
. Значению параметра  на кривой
на кривой . Таким образом, каждое разбиение
. Таким образом, каждое разбиение  отрезка задает ломаную
отрезка задает ломаную 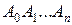 , вписанную в данную кривую.
, вписанную в данную кривую. длину этой вписанной ломаной. Тогда, по определению, длина кривой – это точная верхняя грань длин всевозможных вписанных в кривую ломаных
длину этой вписанной ломаной. Тогда, по определению, длина кривой – это точная верхняя грань длин всевозможных вписанных в кривую ломаных  .
. переменную длину дуги на отрезке
переменную длину дуги на отрезке  .
. . Отсюда длина дуги, соответствующая изменению параметра
. Отсюда длина дуги, соответствующая изменению параметра  (8.1)
(8.1) Пример. Найти длину одной арки циклоиды.
Пример. Найти длину одной арки циклоиды.
 . Найдем производные координатных функций:
. Найдем производные координатных функций:  .
.
 .
. и графиком функции
и графиком функции  .
. - непрерывна, то криволинейный сектор – квадрируемая фигура и площадь его находится по формуле
- непрерывна, то криволинейный сектор – квадрируемая фигура и площадь его находится по формуле .
. конечным набором точек
конечным набором точек
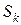 часть площади криволинейного сектора, ограниченного линиями
часть площади криволинейного сектора, ограниченного линиями  ,
,  достаточно мала, то
достаточно мала, то  и радиусом
и радиусом  , где
, где  произвольная точка из интервала
произвольная точка из интервала  . Тогда верно приближенное равенство
. Тогда верно приближенное равенство 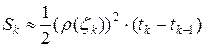 . А так как площадь криволинейного сектора равна
. А так как площадь криволинейного сектора равна  , то получаем приближенное равенство
, то получаем приближенное равенство .
. .
. интегральные суммы стремятся к интегралу Римана. Таким образом получаем формулу
интегральные суммы стремятся к интегралу Римана. Таким образом получаем формулу  .
. Пример. Найти площадь фигуры, ограниченной лемнискатой Бернулли, задаваемой уравнением
Пример. Найти площадь фигуры, ограниченной лемнискатой Бернулли, задаваемой уравнением  .
. . Тогда уравнение кривой примет вид
. Тогда уравнение кривой примет вид 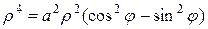 или
или  .
.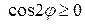 .
. .
. , значит ее график симметричен относительно начала координат.
, значит ее график симметричен относительно начала координат. , то график функции также симметричен относительно оси
, то график функции также симметричен относительно оси  . Тогда площадь фигуры, ограниченной лемнискатой
. Тогда площадь фигуры, ограниченной лемнискатой  .
. , где
, где  – множество всех многогранников, лежащих внутри
– множество всех многогранников, лежащих внутри  , где
, где  – множество всех многогранников, содержащих в себе
– множество всех многогранников, содержащих в себе  , тогда объем тела равен
, тогда объем тела равен  .
.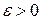 найдутся многогранники
найдутся многогранники  и
и  такие что
такие что  и
и  .
.
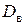 получено из нижнего основания
получено из нижнего основания  сдвигом на вектор
сдвигом на вектор  , перпендикулярный нижнему основанию (при этом, конечно, фигуры
, перпендикулярный нижнему основанию (при этом, конечно, фигуры  , где
, где  – высота призмы, то есть длина вектора
– высота призмы, то есть длина вектора  найдутся многоугольники
найдутся многоугольники  и
и  такие, что
такие, что 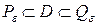 и
и  . Многогранник с высотой
. Многогранник с высотой  лежит внутри призмы, а многогранник с основанием
лежит внутри призмы, а многогранник с основанием 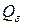 и высотой
и высотой  .
. . С другой стороны,
. С другой стороны,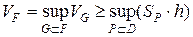 . Отсюда видно, что
. Отсюда видно, что  Рассмотрим тело, которое получается при вращении криволинейной трапеции, ограниченной сверху графиком функции
Рассмотрим тело, которое получается при вращении криволинейной трапеции, ограниченной сверху графиком функции 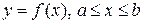 , вокруг оси
, вокруг оси  получается круг радиуса
получается круг радиуса  . Тогда его площадь
. Тогда его площадь  . Соответственно
. Соответственно – объем тела вращения вокруг оси
– объем тела вращения вокруг оси 
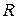 и высотой
и высотой  .
. , где
, где  . Подставляя
. Подставляя 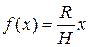 в формулу объема тела вращения, получаем
в формулу объема тела вращения, получаем .
. , формула имеет вид
, формула имеет вид  .
.

 до
до  . Подставив в формулу вычисления объема, получим
. Подставив в формулу вычисления объема, получим  .
. .
. ; при
; при  . Отсюда:
. Отсюда:
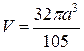 .
. .
.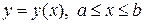 . Ордината центра тяжести кривой находится по формуле
. Ордината центра тяжести кривой находится по формуле  . Подставив сюда формулу для нахождения статического момента и умножив это равенство на длину кривой
. Подставив сюда формулу для нахождения статического момента и умножив это равенство на длину кривой  , получаем
, получаем .
. :
: .
.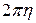 , которую описывает центр тяжести. Теорема доказана.
, которую описывает центр тяжести. Теорема доказана. В силу симметрии абсцисса центра тяжести
В силу симметрии абсцисса центра тяжести  . Найдем ординату центра тяжести, используя первую теорему Паппа-Гульдина. Поверхность, образованная при вращении кривой вокруг оси
. Найдем ординату центра тяжести, используя первую теорему Паппа-Гульдина. Поверхность, образованная при вращении кривой вокруг оси  . Длина кривой равна половине длины окружности
. Длина кривой равна половине длины окружности  . Подставив эти значения в формулу
. Подставив эти значения в формулу  , найдем ординату центра тяжести
, найдем ординату центра тяжести  .
. Используем результат, полученный в предыдущем примере. Ордината центра тяжести полуокружности
Используем результат, полученный в предыдущем примере. Ордината центра тяжести полуокружности  .
. . Из первой теоремы Паппа-Гульдина имеем формулу
. Из первой теоремы Паппа-Гульдина имеем формулу 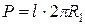 . Отсюда искомая площадь поверхности
. Отсюда искомая площадь поверхности .
. .
. . Применяя формулу для вычисления статического момента
. Применяя формулу для вычисления статического момента  , получаем
, получаем  . Домножим на число
. Домножим на число  .
.


