
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема 3. Формула Ньютона – Лейбница.Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Пусть функция Функция Тогда
Доказательство. Из теоремы 2 следует, что интеграл с переменным верхним пределом является первообразной функции Найдем костанту С. Положим в последнем равенстве
Полагая в этом равенстве
7.2. Правило интегрирования по частям в определённом интеграле. Пусть функции
Пример 1. Вычислить интеграл Обозначим через
Подставляя эти выражения в формулу интегрирования по частям, получаем
Пример 2. Вывести рекуррентную формулу для вычисления интеграла
Обозначим через
Подставляя эти выражения в формулу интегрирования по частям, получаем
Воспользовавшись основным тригонометрическим тождеством
Отсюда находим рекуррентную формулу для вычисления искомого интеграла Начальные значения интегралов для этой формулы Пример 3. Вычислить интегралы Применим рекуррентную формулу, выведенную в примере 2, при
Учитывая, что Применим рекуррентную формулу, выведенную в примере 2, при
Учитывая, что
7.3. Замена переменной в определённом интеграле.
Пусть функция Функция
Пример 1. Вычислить интеграл Первый способ. Перепишем подынтегральную функцию в виде
Этот интеграл является интегралом от дифференциального бинома
Число число Возводим в квадрат и выражаем подынтегральные выражения
Пересчитаем пределы интегрирования из формулы при Подставляя эти выражения в первоначальный интеграл, получаем
Второй способ. В этом интеграле можно избавиться от иррациональности с помощью тригонометрической подстановки. Сделаем замену
Пересчитаем пределы интегрирования. Если если
Сделаем еще одну замену переменной Если
Отметим два основных отличия замены переменной в определённом интеграле от замены переменной в неопределённом интеграле: 1) надо пересчитывать пределы интегрирования; 2) не нужно возвращаться к старой переменной.
Следующий пример показывает, что формальное применение формулы замены переменной, без учета условий ее применимости, может привести к неверному результату. Пример 2. Интеграл Это произошло потому, что при изменении переменной новая переменная
При замене переменной определенный интеграл Римана может перейти в несобственный интеграл и наоборот. Поэтому введем понятие несобственного интеграла. Позднее этот интеграл будет изучаться более подробно.
7.4. Несобственный интеграл Интеграл Римана рассматривается от ограниченной функции на отрезке. Этот интеграл можно обобщить в двух направлениях: сделать неограниченным промежуток или функцию неограниченной.
Несобственный интеграл первого рода – это интеграл по неограниченому промежутку. Пусть функция
Возможны следующие случаи. Если предел существует и конечен, то говорят, что несобственный интеграл сходится. Если же предел равен бесконечности или вообще не существует, то говорят, что несобственный интеграл расходится.
Пример 1. Исследовать на сходимость в зависимости от параметра Рассмотрим сначала случай, когда
В этом случае интеграл расходится. Пусть теперь
Итак, Это важный интеграл, он широко используется при исследовании на сходимость других несобственных интегралов, а также в теории рядов.
Пример 2. Исследовать на сходимость несобственный интеграл Запишем несобственный интеграл по определению
Полученный предел не существует, следовательно, интеграл расходится.
|
||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 407; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.92.213 (0.01 с.) |

 непрерывна на отрезке
непрерывна на отрезке  .
. любая из первообразных функции
любая из первообразных функции  .
. также является первообразной и две различные первообразные отличаются только на константу, то
также является первообразной и две различные первообразные отличаются только на константу, то 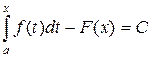 . (1)
. (1) :
: . Отсюда находим значение константы
. Отсюда находим значение константы  . Подставив его в равенство (1), получаем
. Подставив его в равенство (1), получаем .
. , получаем искомую формулу
, получаем искомую формулу  .
. и
и  имеют непрерывные производные на отрезке
имеют непрерывные производные на отрезке 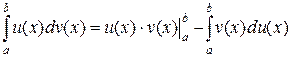 .
. .
.
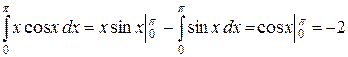 .
. .
.
 .
. , сводим вычисление данного интеграла к таким же интегралам меньшего порядка
, сводим вычисление данного интеграла к таким же интегралам меньшего порядка
 .
.

 :
: .
. , получаем
, получаем  .
.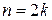 :
: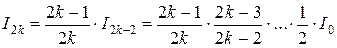 .
. , получаем
, получаем 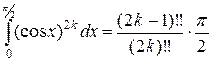 .
. определена и непрерывна на отрезке
определена и непрерывна на отрезке  .
. определена и непрерывна вместе со своей производной на отрезке
определена и непрерывна вместе со своей производной на отрезке  ,
,  ,
, 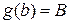 . Тогда справедлива формула замены переменной
. Тогда справедлива формула замены переменной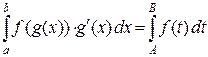 , где
, где  .
.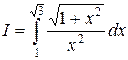 .
. .
. . В данном примере
. В данном примере  .
. не является целым; число
не является целым; число  также не является целым;
также не является целым;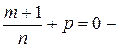 целое. Значит, исходя из общей теории, подходит подстановка
целое. Значит, исходя из общей теории, подходит подстановка 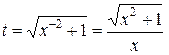 .
.
 :
: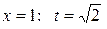 ; при
; при  .
.

 , то
, то  ;
; , то
, то 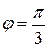 . Подставляя эти значения в интеграл, получаем
. Подставляя эти значения в интеграл, получаем .
. .
. ; если
; если  . Тогда
. Тогда
 . Сделаем в этом интеграле замену
. Сделаем в этом интеграле замену  . Тогда
. Тогда  . Получили противоречие, так как один и тот же интеграл не может принимать два разных значения.
. Получили противоречие, так как один и тот же интеграл не может принимать два разных значения.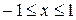
 изменяется на лучах
изменяется на лучах  . А согласно теореме о замене переменной она должна изменяться на отрезке
. А согласно теореме о замене переменной она должна изменяться на отрезке  .
. . Несобственным интегралом от функции
. Несобственным интегралом от функции 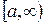 называется следующий предел от определенного интеграла
называется следующий предел от определенного интеграла .
. .
. .Тогда
.Тогда .
. . Тогда
. Тогда
 сходится при
сходится при  и расходится при
и расходится при  .
. .
. .
.


