
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основні поняття та формули теорії ймовірностейСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
ТЕОРІЯ ЙМОВІРНОСТЕЙ МЕТОДИЧНІ ВКАЗІВКИ до практичних занять, індивідуальної та самостійної роботи з варіантами завдань для розрахунково-графічної роботи
Для підготовки бакалаврів галузей знань 0305 «Економіка і підприємництво», 0306 «Менеджмент і адміністрування» заочної форми навчання у вищих навчальних закладах Мінагрополітики України.
Луганськ-2011 УДК 681.513:62-50
Укладачі:
ЛЄВІ ЛЕОНІД ІСААКОВИЧ, доктор технічних наук, професор, завідувач кафедри фізико-математичних дисциплін. ТАЩІЛІН МАКСИМ ВАСИЛЬОВИЧ, кандидат технічних наук, доцент кафедри фізико-математичних дисциплін. Тащіліна Анастасія Віталіївна, асистент кафедри фізико-математичних дисциплін
Теорія ймовірностей. Методичні вказівки до практичних занять, індивідуальної та самостійної роботи з варіантами завдань для розрахунково-графічної роботи. Для підготовки бакалаврів галузей знань 0305 «Економіка і підприємництво», 0306 «Менеджмент і адміністрування» у вищих навчальних закладах Мінагрополітики України./ Лєві Л.І., Тащілін М.В., Тащіліна А.В. – Луганськ, Вид-во ЛНАУ, 2011. – 73 с.
Рецензенти:
Грібанов В.М. доктор технічних наук, професор, завідувач кафедри прикладної математики Східноукраїнського національного університету ім. В.Даля;
Коваль А.В. кандидат фізико-математичних наук, доцент кафедри фізико-математичних дисциплін Луганського національного аграрного університету.
Видання розглянуто і рекомендовано до друку на засіданні кафедри фізико-математичних дисциплін (протокол № 5 від 11 січня 2011 р.); на засіданні методичної комісії економічного факультету (протокол №5 від 14 січня 2011 р.). ЗМІСТ
РОБОЧА ПРОГРАМА Навчальної дисципліни
І. Випадкові події Основні поняття та формули теорії ймовірностей 1.1. Поняття “випробування” та “подія”. Класифікація подій. 1.2. Операції над подіями. 1.3. Елементи комбінаторики. 1.4. Класичне означення ймовірності. 1.5. Геометрична ймовірність. 1.6. Відносна частота та статистичне означення ймовірності. Основні теореми теорії ймовірностей 1.7. Теорема про ймовірність суми скінченного числа несумісних подій. 1.8. Теореми множення ймовірностей. Умовна ймовірність. 1.9. Незалежні події. Теорема множення для незалежних подій. 1.10. Ймовірність появи хоча б однієї з подій. 1.11. Теорема додавання ймовірностей сумісних подій. 1.12. Формула повної ймовірності. Формула Баєса. Схема повторних незалежних випробувань 1.13. Формула Бернуллі. 1.14. Найімовірніше число появи події 1.15. Формула Пуассона. 1.16. Локальна теорема Муавра-Лапласа. 1.17. Інтегральна теорема Муавра-Лапласа. ІІ. Випадкові величини 2.1. Класифікація випадкових величин. 2.2. Закони розподілу випадкових величин. 2.3. Функції розподілу випадкових величин та їх властивості. 2.3.1. Інтегральна функція розподілу. 2.3.2. Диференціальна функція розподілу. ВИПАДКОВІ ПОДІЇ
ОЗНАЧЕННЯ ЙМОВІРНОСТІ ПОДІЇ. БЕЗПОСЕРЕДНЄ ОБЧИСЛЕННЯ ІМОВІРНОСТЕЙ Ймовірністю події А називається числова міра об’єктивної можливості настання цієї події в певному випробуванні. Позначається така ймовірність Р (А). Властивості ймовірності 1. Ймовірність достовірної події 2. Ймовірність неможливої події 3. Ймовірність будь-якої випадкової події Класичне означення ймовірності. Ймовірністю випадкової події А називається відношення кількості елементарних подій m, які сприяють появі цієї події (становлять множину її елементарних подій), до загальної кількості n рівноможливих елементарних подій:
Розв’язання. а) Позначимо А = {вибраний чоловік-адміністратор} У банку працюють 100 чоловік, n = 100. З них 15 — чоловіки-адміністратори, m = 15, отже Р (A)= 15/100 = 0,15. б) B = {вибрана жінка-операціоніст } 35 службовців у банку — жінки-операціоністи, отже P (В) = 35/100 = 0,35. в) С = {вибраний чоловік} 40 службовців банку — чоловіки, отже Р (С)= 40/100 = 0,40. г) D = { вибраний операціоніст} Із загальної кількості службовців банку 60 — операціоністи, отже P (D)= 60/100= 0,60.
Елементи комбінаторики Розміщення. Кінцеві впорядковані підмножини, що містять m елементів, узятих з n елементів основної множини, називаються розміщеннями з n елементів по m елементів. Число всіх можливих розміщень з n елементів по m позначають
Перестановки. Різні кінцеві впорядковані множини, що складаються зі всіх елементів деякої заданої множини називаються перестановками. Якщо основна множина містить n елементів, то число перестановок позначається
Сполучення. Кінцеві невпорядковані підмножини, які містять m різних елементів з n елементів заданої множини називаються сполученнями з n елементів по m. Число сполучень з n елементів по m позначають
Розміщення із повторенням. Беремо з множини навмання m елементів з поверненням. Тоді у фіксованій підмножині кожний елемент може повторитися m разів. Елементарною подією у випробуванні буде розміщення з n елементів по m із повторенням, а кількість таких розміщень
Перестановки із повторенням. Маємо
Сполучення з повтореннями. Якщо в сполученнях з n елементів по m деякі з елементів (і навіть всі) можуть виявитися однаковими, то такі поєднання називаються сполученнями з повтореннями із n елементів по m. Число сполучень з повтореннями із n елементів по m позначається символом
Розв’язання. Позначимо Випробуванням є відбір 6 чоловік з 10 акціонерів. Число всіх результатів випробування дорівнює числу сполучень з 10 по 6, тобто
Результатом, що сприяє події А, є відбір шести чоловік серед семи акціонерів, які не мають привілейованих акцій. Число всіх результатів, що сприяють події А, буде Шукана ймовірність
Питання для самоконтролю
1. Що розуміють під випробуванням, подією? 2. Що називається сумою подій, добутком подій, різницею подій? 3. Які події називаються несумісними? 4. Дати означення повної групи несумісних подій. 5. Які події називаються рівноможливими? 6. Дати означення: а) перестановки з п елементів; б) розміщення з п по m елементів; в) сполучення з п по m елементів. 7. Записати формули для обчислення числа: а) перестановок з п елементів; б) розміщень з п по m елементів; в) сполучень з п по m елементів. 8. Дати означення класичної ймовірності (навести приклади). 9. Сформулювати властивості ймовірності.
Завдання 1 1.1. Керівництво фірми виділило відділу реклами кошти для розміщення у пресі оголошень про товари і послуги, що пропонуються фірмою. За підрахунками відділу реклами виділених коштів вистачить для того, щоб розмістити оголошення лише в 10 з 25 міських газет. Скільки існує способів випадкового відбору газет для розміщення об’яв? Яка ймовірність того, що навмання вибрані 10 редакцій газет виявляться з числа 15 газет, що мають найбільший тираж? 1.2. Нарада директорів складається з 4 бухгалтерів, 3 менеджерів і 2 інженерів. Планується створити підкомітет із трьох його членів. Знайти ймовірність того, що до підкомітету увійдуть бухгалтер і 2 менеджери. 1.3. Скільки існує способів складання у випадковому порядку списку з 7 кандидатів для вибору на керівну посаду? Яка ймовірність того, що кандидати будуть розставлені у переліку за віком (від молодшого до старшого)? 1.4. У двох з 14 складених касиром рахунків є помилки. Ревізор вирішив перевірити навмання 5 рахунків. Яка ймовірність, що помилки не будуть виявлені? 1.5. До ліфта дев’ятиповерхового офісного центру на 1-у поверсі зайшло троє службовців. Кожен із них з однаковою ймовірністю виходить на будь-якому з поверхів, починаючи з 2-го. Знайти ймовірність того, що всі пасажири вийдуть одночасно на одному з поверхів. 1.6. Купуючи картку лотереї «Спортлото», гравець повинен закреслювати 6 з 49 можливих чисел від 1 до 49. Якщо при розіграші лотереї він вгадає всі 6 чисел, то має шанс виграти значну суму грошей. Скільки можливих комбінацій можна скласти з 49 по 6, якщо порядок чисел байдужий? Чому дорівнює ймовірність вгадати всі 6 номерів? 1.7. Магазин отримує товар партіями по 100 штук. Якщо п'ять узятих навмання зразків відповідають стандартам, партія товару поступає на реалізацію. У черговій партії 8 одиниць товару з дефектом. Знайти ймовірність того, що товар поступить на реалізацію. 1.8. Дев'ять запечатаних пакетів з пропозиціями ціни на оренду ділянок для буріння нафтових свердловин поступили вранці в спеціальне агентство ранковою поштою. Скільки існує різних способів черговості відкриття конвертів з пропозиціями ціни? Яка ймовірність того, що конверти випадково виявляться розкритими в залежності від величини пропонованої за оренду ділянок ціни (в порядку зростаючої вартості)? 1.9. На курсах підвищення кваліфікації бухгалтерів навчають визначати правильність оформлення накладної. Для перевірки викладач пропонує перевірити 12 накладних, 5 з яких містять помилки. Навмання вибирають три накладних. Знайти ймовірність того, що з трьох накладних одна з помилками. 1.10. Скільки існує способів складання списку 10 ділових дзвінків випадковим чином? Яка ймовірність того, що список виявиться складеним в алфавітному порядку? Яка ймовірність того, що список з 6 навмання вибраних із 10 запланованих ділових дзвінків виявиться складеним в алфавітному порядку. 1.11. Фірма потребує організації 4 нових складів. Її співробітники підібрали 8 відповідних однаково зручних приміщень, 5 з яких розташовані в багатоповерхових будівлях. Скільки існує способів відбору 4 приміщень з 8 у випадковому порядку? Яка ймовірність того, що всі відібрані приміщення будуть розташовані в багатоповерхових будівлях? 1.12. Із 12 акціонерних товариств 7 успішно функціонують, 3 на межі банкрутства і 2 є банкротами. Громадянин придбав навмання по одній акції 5 акціонерних товариств. Яка ймовірність того, що серед навмання куплених акцій лише одна буде від товариства-банкрота? 1.13. На ринку представлено 8 різних пакетів програм для бухгалтерії з приблизно рівними можливостями, 4 з яких мають найменший об'єм пам'яті. Для апробації в своїх філіалах фірма вирішила відібрати 3 з них. Скільки існує способів відбору 3 програм з 8, якщо відбір здійснений у випадковому порядку? Яка ймовірність того, що випадково відібрані пакети програм займатимуть найменший об'єм пам'яті? 1.14. На пачках грошових банкнот проставлені номери від 1 до 10 за зростаючою сумою грошей у них. Навмання вибираються 4 з них для перерахунку. Знайти ймовірність, що відібрані пачки банкнот будуть: а) з номерами 4, 2, 6, 8; б) будуть розташовані за зростаючою сумою грошей. 1.15. У регіональному відділенні банку операціоністами працює 30 осіб, серед яких 10 чоловіків. Необхідно вибрати делегацію, що складається з 7 співробітників для підвищення кваліфікації і обміну досвідом з іншими відділеннями банку. Знайти ймовірність того, що серед вибраних будуть 3 чоловіки. 1.16. Компанія реалізує 4 види товарів, розташованих на різних складах. Знайти ймовірність, що для реалізації наступних 3 крупних замовлень від різних клієнтів доведеться виїжджати на різні склади. 1.17. Порада директорів складається з 3 бухгалтерів, 3 менеджерів і 2 інженерів. Планується створити підкомітет з трьох його членів. Знайти ймовірність того, що до підкомітету увійдуть два бухгалтери і менеджер. 1.18. Виділені крупні суми на виконання 4 крупних урядових програм, що обіцяють виконавцям високий прибуток. Скільки існує способів випадкового розподілу цих 4 програм між 6 можливими виконавцями? Яка ймовірність того, що кошти на виконання програм при такому розподілі отримають саме 4 виконавця, що мають найбільший прибуток? 1.19. Брокерська фірма пропонує акції різних компаній. Акції 10 з них продаються за найменшою серед наявних акцій ціною і володіють однаковою прибутковістю. Клієнт збирається придбати акції 3 таких компаній — по 1 від кожної компанії. Мається на увазі, що ціни на акції компаній наступного року зміняться і будуть різними. Скільки існує способів вибору 3 таких акцій з 10, якщо вибір здійснюється у випадковому порядку? Яка ймовірність того, що придбані акції попадуть в число акцій, зростання цін на які буде найбільшим наступного року? 1.20. Фірми F1, F2, F3, F4, F5 пропонують свої умови по виконанню 3 різних контрактів К1, К2 і КЗ. Будь-яка фірма може отримати лише один контракт. Контракти різні, тобто якщо фірма F1 отримає контракт К1, то це не те ж саме, якщо вона отримає контракт К2. Скільки способів здобуття контрактів мають фірми? Якщо передбачити рівноможливість отримання контрактів, чому дорівнює ймовірність того, що фірма F3 отримає контракт? 1.21. Набір трицифрового номера виграшної облігації виконують триразовим викиданням з урни одного за одним трьох жетонів із п’яти, пронумерованих цифрами від 1 до 5. Знайти ймовірність того, що вибраний номер містить цифру 3. 1.22. У малому підприємстві працюють 4 жінки та 5 чоловіків. Випадковим способом 2 особи запізнились. Знайти ймовірність, що одна з цих осіб – жінка, а друга чоловік. 1.23. Касир видає заробітну платню за 4 відомостями. Яка ймовірність того, що 3 робітника, що підійшли випадковим чином, отримають заробітну платню за різними відомостями? 1.24. У рекламному агентстві|агенції| є 5 послуг: поліграфія, дизайн, виробництво рекламних відеороликів, трансляція відеороликів на телебаченні та у супермаркетах. У агентство|агенцію| прийшло 4 замовлення. Знайти ймовірність, що всі замовлення на послуги одного виду. 1.25. У філії банку працюють 15 співробітників, 3 з яких не мають потрібної кваліфікації. Яка ймовірність, що два з трьох навмання відібраних для підвищення кваліфікації співробітника не мають потрібної кваліфікації? 1.26. Консультаційній фірмі пропонують 2 замовлення від першої корпорації і 7 від другої. Експерти фірми вважають, що виконати консультаційна фірма може лише 3 з них. Яка ймовірність того, що з 3 навмання вибраних для розгляду замовлень одне замовлення буде від першої, а два від другої корпорацій? 1.27. Із 20 банків 10 розташовані за межами міста. Для дослідження випадково обрано 5 банків. Яка ймовірність того, що серед обраних у межах міста виявляться 3 банки? 1.28. Брокерська фірма пропонує акції 3 різних компаній за найвищою ціною. Клієнт збирається навмання придбати 5 акцій незалежно від аналізу ситуації на ринку. Яка ймовірність того, що всі придбані акції будуть однієї компанії? 1.29. В торговому підприємстві, що займається реалізацією напоїв, працюють 10 менеджерів, 4 з яких мають певний досвід роботи. Підприємству необхідно для розширення сфери торгівлі у літній період відправити у відрядження 3 менеджера з продаж. Яка ймовірність того, що серед навмання відібраних 2 будуть мати певний досвід роботи? 1.30. У центральну бухгалтерію районного відділу освіти поступають звіти від 10 дитячих садків та 15 шкіл. Яка ймовірність того, що з 4 навмання вибраних для перевірки звітів два будуть з дитячих садків?
Питання для самоконтролю 1. Сформулювати теореми додавання ймовірностей для несумісних і сумісних подій. 2. Які випадкові події називаються: а) незалежними в сукупності; б) попарно незалежними? 3. Дати означення умовної ймовірності випадкової події. 4. Сформулювати теореми множення ймовірностей для залежних і незалежних подій. 5. Записати формулу обчислення ймовірності появи принаймні однієї з п несумісних подій. Завдання 2 2.1. Для отримання кредиту підприємець звертається до двох банків. Ймовірність того, що перший банк не відмовить йому в наданні кредиту, становить 0,7, другий – 0,85. Знайти ймовірність того, що: а) перший або другий банк дасть згоду на кредитування; б) обидва банки відмовляться надати кредит. 2.2. Ймовірність того, що ціна окремої акції зростатиме протягом ділового дня дорівнює 0,4. Якщо природа зміни ціни будь-якого дня є незалежною від того, що сталося попереднього дня (днів), то яка ймовірність того, що ціна: а) зростатиме чотири дні підряд? б) зростатиме два з трьох днів? 2.3. З партії виробів товарознавець навмання відбирає вироби вищого сорту. Ймовірність того, що вибрана річ виявиться вищого сорту дорівнює 0,8; першого сорту – 0,7; другого сорту – 0,5. Знайти ймовірність того, що з трьох наугад відібраних виробів будуть: а) лише два вищого сорту; б) всі різні. 2.4. У двох із 14 складених касиром рахунків є помилки. Ревізор вирішив перевірити навмання 5 рахунків. Яка ймовірність, що помилки будуть виявлені менш ніж в двох? 2.5. Два бухгалтери обробляють рівну кількість рахунків. Ймовірність того, що перший бухгалтер допустить помилку, дорівнює 0,005, для другого ця ймовірність дорівнює 0,01. Знайти ймовірність того, що при перевірці рахунків: а) лише перший бухгалтер допустив помилку; б) помилки допущені не були. 2.6. Податкова декларація на прибуток може перевірятися районною або обласною податковою адміністрацією. Ймовірність того, що податкова декларація перевірятиметься обласною адміністрацією – 0,05, районною – 0,04. Рішення щодо перевірки на обласному і районному рівнях приймаються незалежно: а) яка ймовірність бути перевіреним обома адміністраціями? б) яка ймовірність пройти тільки районну перевірку? в) яка ймовірність не бути перевіреним? 2.7. Ймовірність отримати прибуток з акцій компаній А, В і С для акціонера відповідно дорівнюють 0,6; 0,7; 0,5. Знайти ймовірність того, що: а) лише один вид акцій складе прибуток акціонера, б) хоча б один вид акцій принесе прибуток їх володареві. 2.8. Ймовірність банкрутства для першої фірми - це додатний розв’язок рівняння 2.9. Ймовірність своєчасної сплати податків для першого підприємства дорівнює 0,8, для другого - 0,6, для третього - 2/3. Визначити ймовірність своєчасної сплати податків а) не більше ніж одним підприємством; б) тільки одним підприємством. 2.10. В об’єднання входять три підприємства. Ймовірність виконати план для першого підприємства дорівнює 0,8, для другого – 0,9, для третього – 0,85. Знайти ймовірність таких подій: а) договір виконає лише одне підприємство; б) договір виконають всі підприємства. 2.11. Ймовірність прибуткової діяльності для першої фірми дорівнює 0,7, для другої - 0,5, для третьої ця ймовірність у три рази менша від суми ймовірностей для першої та другої фірм. Знайти ймовірність того, що прибутковими будуть а) дві фірми; б) хоча б одна фірма. 2.12. На курсах підвищення кваліфікації бухгалтерів навчають визначати правильність оформлення накладної. Для перевірки викладач пропонує перевірити 12 накладних, 5 з яких містять помилки. Навмання вибирають три накладних. Яка ймовірність того, що з трьох накладних не менше двох з помилками? 2.13. Надійність першого банку – 0,95; для другого – 0,8; для третього – 0,85. Підприємець зробив вклад в усі три банки. Знайти ймовірність того, що підприємцеві повернуть вклад: а) два банки; б) хоча б один банк. 2.14. Ймовірність виконання договору для першого підприємства становить 3/5, для другого ця ймовірність є розв’язком рівняння 2.15. Ймовірність повного розрахунку за енергоносії для першого заводу дорівнює 0,5, для другого - на 20 % більша. Знайти ймовірність своєчасної сплати за енергоносії: а) одним заводом; б) двома заводами. 2.16. Ймовірність виконання договору для першої фірми є розв’язком рівняння 2.17. Ймовірність повної сплати податків для першого підприємства 4/5, для другого ця ймовірність задовольняє рівнянню 2.18. Ймовірність банкрутства для першої фабрики дорівнює 0,2, для другої - на 50 % більша ніж для першої, для третьої дана ймовірність є розв’язком рівняння 2.19. Ймовірність виконання договору для першого підприємства 2/5, для другого - 0,8, для третього ця ймовірність становить 60 % від суми ймовірностей першого та другого підприємств. Знайти ймовірність виконання договору тільки двома підприємствами. 2.20. Ймовірність того, що в певний день торгівельній базі буде потрібна двухтонна машина, дорівнює 0,9, п'ятитонна – 0,7. Визначити ймовірність того, що торгівельній базі буде потрібна: а) двухтонна і п'ятитонна машина; б) жодна з них; в) хоча б одна автомашина. 2.21. Перша фірма може одержати заданий прибуток з ймовірністю 0,7, для другої ця ймовірність є розв’язком рівняння 2.22. Ймовірність ліквідації заборгованості для першого заводу дорівнює 6/7, для другого - 3/4, для третього - 0,8. Знайти ймовірність ліквідації заборгованості хоча б двома заводами. 2.23. Ймовірність того, що податкова інспекція пред'явить штраф першому підприємству – 0,2, другому – 0,3, третьому – 0,15. Знайти ймовірність того, що будуть оштрафовані: а) три підприємства; б) два підприємства. 2.24. Технологічний процес складається з декількох операцій. Ймовірність того, що під час першої операції виріб отримає пошкодження, дорівнює 0,1, а під час другої операції – 0,05. Яка ймовірність того, що після двох операцій виріб виявиться а) пошкодженим; б) непошкодженим? 2.25. Банк може видати кредит одному з трьох клієнтів з ймовірністю 2.26. Ймовірність своєчасного складання звіту для першого економіста дорівнює 0,9, для другого ця ймовірність є додатним коренем рівняння 2.27. Заводом відправлена автомашина за різними матеріалами на чотири бази. Ймовірність наявності потрібного матеріалу на першій базі дорівнює 0,9, на другій – 0,95, на третій – 0,8, на четвертій – 0,6. Знайти ймовірність того, що лише на одній базі не виявиться потрібного матеріалу. 2.28. Ймовірності своєчасного повернення кредитів кожним з трьох позичальників банку відповідно дорівнюють: 0,6; 0,9; 0,7. Знайти ймовірність наступних подій: а) лише два позичальники повернуть кредит своєчасно; б) хоча б один з позичальників поверне кредит своєчасно. 2.29. Ймовірності виконання договору для першого та другого підприємств задовольняють системі рівнянь Знайти ймовірність виконання договору тільки одним підприємством. 2.30. В об’єднання входять три підприємства. Ймовірність виконати план для першого підприємства дорівнює 0,8, для другого – 0,9, для третього – 0,85. Знайти ймовірність таких подій: а) договір виконують 2 підприємства; б) договір не виконає жодне підприємство. Питання для самоконтролю
1. Дати поняття повної групи подій. 2. Записати формулу повної ймовірності. 3. Записати формулу Баєса. Для чого служить ця формула? 4. Коли застосовують формулу Баєса? 5. Чому події, що утворюють повну групу у формулі Баєса називають гіпотезами? Завдання 3 3.1. Ймовірність того, що клієнт банку не поверне позику в період економічного зростання, дорівнює 0,04, в період економічної кризи – 0,13. Передбачимо, що ймовірність того, що почнеться період економічного зростання, дорівнює 0,65. Чому дорівнює ймовірність того, що випадково вибраний клієнт банку не поверне отриманий кредит? 3.2. При злитті акціонерного капіталу двох фірм аналітики фірми, яка одержує контрольний пакет акцій, вважають, що операція принесе успіх з ймовірністю, що дорівнює 0,65, якщо голова наради директорів фірми, що поглинається, вийде у відставку; якщо він відмовиться, то ймовірність успіху дорівнює 0,3. Передбачається, що ймовірність відходу у відставку голови складає 0,7. Чому дорівнює ймовірність успіху операції? 3.3. Агент по нерухомості намагається продати ділянку землі під забудову. Він вважає, що ділянка буде продана протягом найближчих шести місяців з ймовірністю 0,9 (якщо економічна ситуація в регіоні не погіршуватиметься). Якщо ж економічна ситуація погіршуватиметься, то ймовірність продати ділянку зменшиться до 0,5. Економіст, що консультує агента, вважає, що з ймовірністю 0,7 економічна ситуація в регіоні протягом наступних шести місяців погіршуватиметься. Чому дорівнює ймовірність того, що ділянка буде продана протягом найближчих шести місяців? 3.4. У корпорації обговорюється маркетинг нового продукту, що випускається на ринок. Виконавчий директор корпорації бажав би, аби новий товар перевершував за своїми характеристиками відповідні товари конкуруючих фірм. Ґрунтуючись на попередніх оцінках експертів, він визначає ймовірність того, що новий товар має більш високу якість в порівнянні з аналогічними, як 0,5, такої ж якості — як 0,3, гірше за якістю — 0,2. Аналіз ринку показав, що новий товар конкурентоздатний. З попереднього досвіду проведення опитування виходить, що якщо товар дійсно конкурентоздатний, то передбачення такого ж висновку має ймовірність 0,7. Якщо товар такий же, як і аналогічні, то ймовірність того, що опитування вкаже на його перевагу, дорівнює 0,4. І якщо товар нижчої якості, то ймовірність того, що опитування вкаже на його конкурентоспроможність, дорівнює 0,2. З врахуванням результату опитування оцініть ймовірність того, що товар дійсно вищої якості і, отже, володіє вищою конкурентоспроможністю, ніж аналогічні. 3.5. Ймовірність того, що новий товар матиме попит на ринку, якщо конкурент не випустить в продаж аналогічний продукт, дорівнює 0,67. Ймовірність того, що товар буде користуватися попитом за наявності на ринку товару, що конкурує, дорівнює 0,42. Ймовірність того, що конкуруюча фірма випустить аналогічний товар на ринок протягом періоду, що цікавить нас, дорівнює 0,35. Чому дорівнює ймовірність того, що товар матиме успіх? 3.6. Три організації представили в контрольне управління рахунки для вибіркової перевірки: перша – 10 рахунків, друга – 20, третя – 15. Ймовірність правильного оформлення рахунків для цих організацій відповідно дорівнює: 0,95; 0,8; 0,9. Яка ймовірність того, що вибраний рахунок правильний? Визначити ймовірність того, що цей рахунок належить третій організації. 3.7. Страхова компанія розділяє застрахованих за класами ризиків: I клас — малий ризик, II клас — середній, III клас — великий ризик. Серед цих клієнтів 50% — першого класу ризику, 30% — другого і 20% — третього. Ймовірність необхідності виплачувати страхову винагороду для першого класу ризику дорівнює 0,01, другого — 0,03, третього — 0,08. Яка ймовірність того, що: а) застрахований отримає грошову винагороду за період страхування; б) що отримав грошову винагороду застрахований, який відноситься до групи малого ризику? 3.8. Судноплавна компанія організовує середземноморські круїзи протягом літнього часу і проводить декілька круїзів за сезон. Оскільки в цьому виді бізнесу дуже висока конкуренція, то бажано, аби всі каюти корабля були повністю зайняті туристами, тоді компанія отримає прибуток. Експерт по туризму, найнятий компанією, передбачає, що ймовірність того, що корабель буде повний протягом сезону, дорівнює 0,92, якщо долар не подорожчає по відношенню до гривні, і з ймовірністю 0,75, якщо долар подорожчає. За оцінками економістів, ймовірність того, що протягом сезону долар подорожчає по відношенню до гривні, дорівнює 0,23. Чому дорівнює ймовір
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 777; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.67.237 (0.014 с.) |

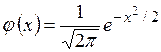 …………………………
…………………………
 ……………
……………


 (1.1)
(1.1) .
. (1.2)
(1.2) .
.
 . Перестановки – не що інше, як спосіб впорядкування якої-небудь кінцевої множини.
. Перестановки – не що інше, як спосіб впорядкування якої-небудь кінцевої множини. (1.3)
(1.3) .
.
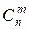 . Воно дорівнює кількості способів, скількома можна витягувати m предметів з n можливих, якщо порядок ролі не грає, і обчислюється за формулою (0 £ m £ n):
. Воно дорівнює кількості способів, скількома можна витягувати m предметів з n можливих, якщо порядок ролі не грає, і обчислюється за формулою (0 £ m £ n): (1.4)
(1.4)
 (1.5)
(1.5) , що співпадає з результатом приведеного прикладу.
, що співпадає з результатом приведеного прикладу.
 елементів, серед яких один елемент повторюється
елементів, серед яких один елемент повторюється  раз, інший елемент повторюється
раз, інший елемент повторюється  раз, і так далі, а останній елемент повторюється
раз, і так далі, а останній елемент повторюється  раз, причому
раз, причому  . Число перестановок з повтореннями позначається
. Число перестановок з повтореннями позначається  та обчислюється за формулою
та обчислюється за формулою (1.6)
(1.6) , що співпадає з результатом приведеного прикладу.
, що співпадає з результатом приведеного прикладу.
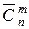 і обчислюється за формулою
і обчислюється за формулою . (1.7)
. (1.7) , що співпадає з результатом приведеного прикладу.
, що співпадає з результатом приведеного прикладу.
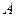 = {серед шести чоловік немає жодного з привілейованими акціями}.
= {серед шести чоловік немає жодного з привілейованими акціями}.

 .
. для другої фірми ця ймовірність на 25 % більша. Знайти ймовірність того, що із двох фірм збанкрутує: а) лише одна, б) хоча б одна.
для другої фірми ця ймовірність на 25 % більша. Знайти ймовірність того, що із двох фірм збанкрутує: а) лише одна, б) хоча б одна. Визначити ймовірність виконання договору: а) одним підприємством; б) хоча б одним підприємством.
Визначити ймовірність виконання договору: а) одним підприємством; б) хоча б одним підприємством. , для другої ця ймовірність дорівнює 0,8. Яка ймовірність виконання договору не більше ніж однією фірмою? Обома фірмами?
, для другої ця ймовірність дорівнює 0,8. Яка ймовірність виконання договору не більше ніж однією фірмою? Обома фірмами? . Знайти ймовірність повної сплати податків одним підприємством.
. Знайти ймовірність повної сплати податків одним підприємством. . Визначити ймовірність банкрутства тільки однієї фабрики.
. Визначити ймовірність банкрутства тільки однієї фабрики. Визначити ймовірність одержання заданого прибутку: а) принаймні однією фірмою, б) тільки однією фірмою.
Визначити ймовірність одержання заданого прибутку: а) принаймні однією фірмою, б) тільки однією фірмою. відповідно. Знайти ймовірність того, що кредит отримає: а) лише один клієнт; б) усі клієнти.
відповідно. Знайти ймовірність того, що кредит отримає: а) лише один клієнт; б) усі клієнти. Яка ймовірність несвоєчасного складання звіту двома економістами.
Яка ймовірність несвоєчасного складання звіту двома економістами.



